1. Convolution
Convolution(합성곱)은 입력 데이터에서 중요한 특성만 골라내기 위해 수행하는 연산을 말한다. 기존에 만들었던 ANN이나 DNN의 밀집층에는 입력-출력 쌍의 개수만큼 가중치가 존재했다. 즉, 가중치가 모든 입력에 대해 곱해진다는 것이다.
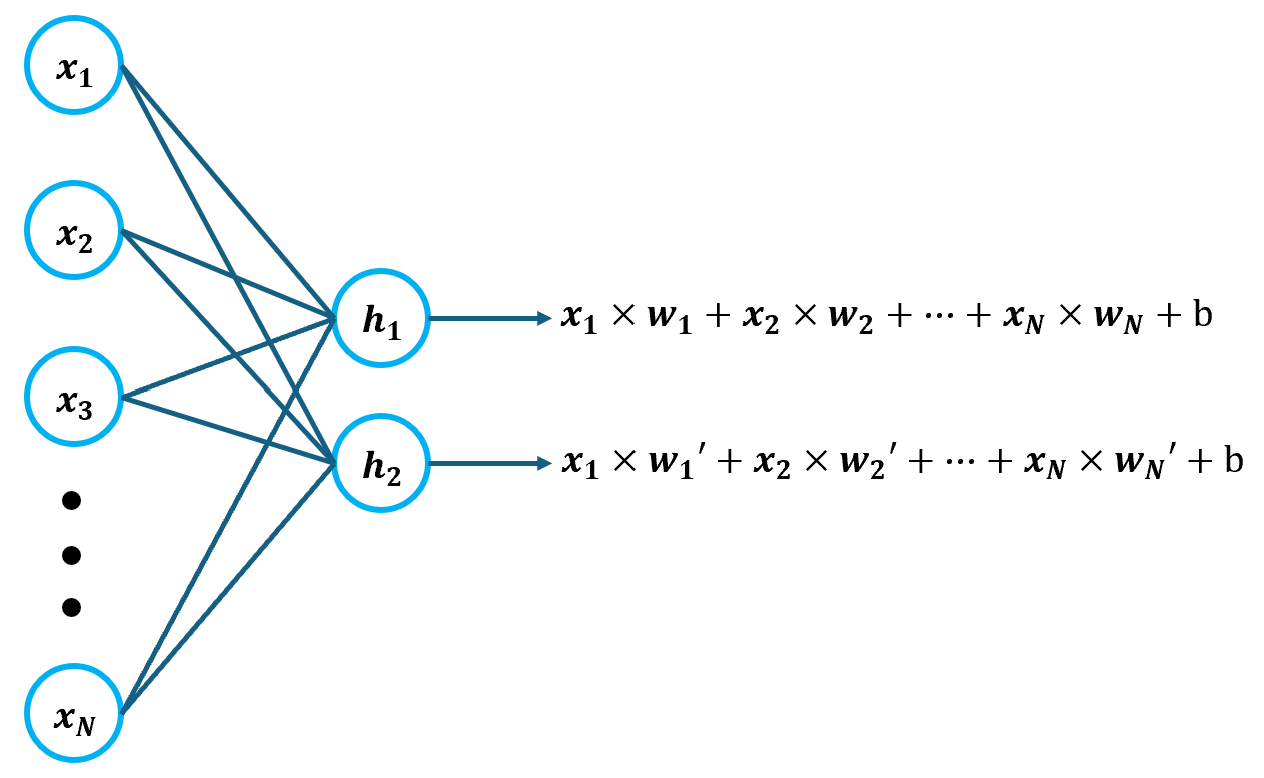
이 때, 출력 값의 개수는 밀집층에 존재하는 뉴런의 개수와 같다. 하지만, Convolution의 경우 입력 데이터 전체가 아닌, 일부에만 가중치를 적용한다. 또한, 가중치의 개수와 크기는 항상 동일하게 고정되어 있다. 예를 들어, 가중치 3개를 갖는 뉴런의 Convolution은 아래와 같이 계산된다.
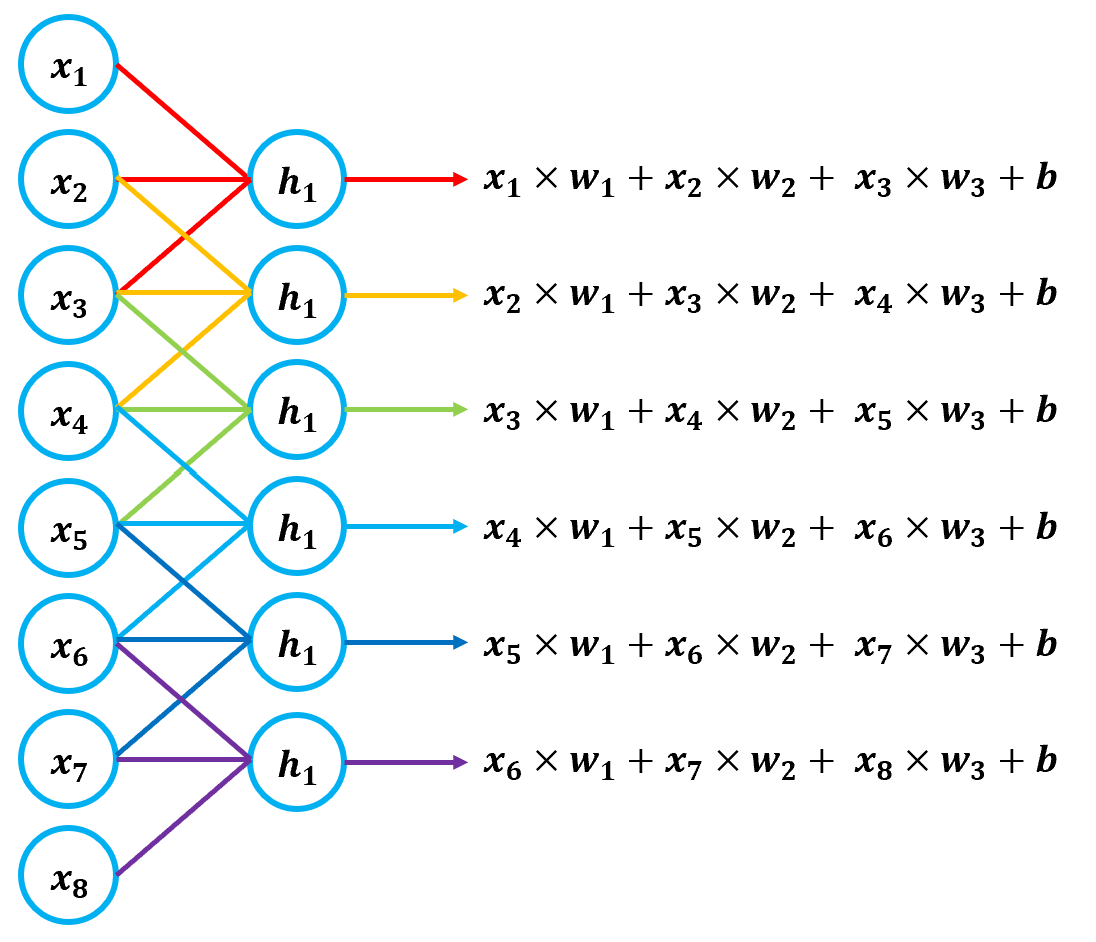
기존 밀집층의 뉴런에서 입력 개수만큼의 가중치로 1개의 출력을 만들었던 것과 달리, Convolution Layer의 뉴런은 3개의 가중치만 이용하여 출력을 만들어낸다. 이러한 동작 방식을 슬라이딩 윈도우라고 하는데, 이 때의 윈도우 사이즈는 하이퍼파라미터가 된다.
이와 같은 구조로 구성되는 인공 신경망을 Convolution Neural Network(CNN, 합성곱 신경망)라 부른다. 또한, CNN의 뉴런은 일반적인 인공 신경망에서의 뉴런과 다르다는 의미로, Filter 또는 Kernel이라고 불린다.
CNN의 가장 큰 장점은 2차원 입력 데이터를 처리할 수 있다는 것이다. 기존의 ANN이나 DNN에서 2차원 입력을 사용하려면 반드시 1차원으로 Flattening 했어야 하지만, CNN에서는 이러한 사전 작업 없이 바로 2차원 입력을 사용할 수 있다.
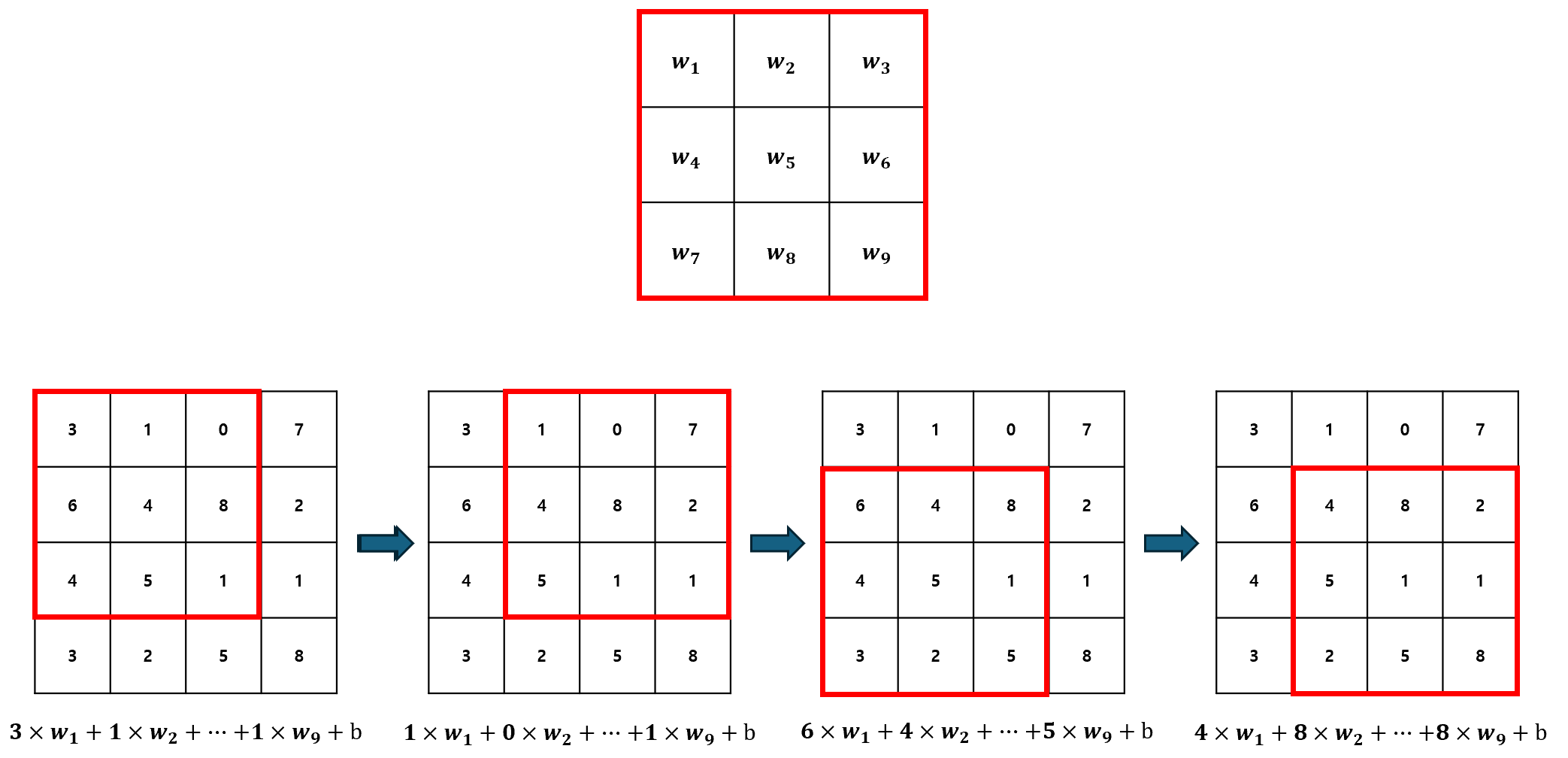
Convolution을 수행한 결과를 2차원으로 나타낸 것을 Feature Map(특성 맵)이라 한다. 이 과정에서 (4, 4)의 입력 데이터가 (2, 2)의 특성 맵으로 변환되기 때문에, 사이즈를 압축하는 것으로 볼 수도 있다.
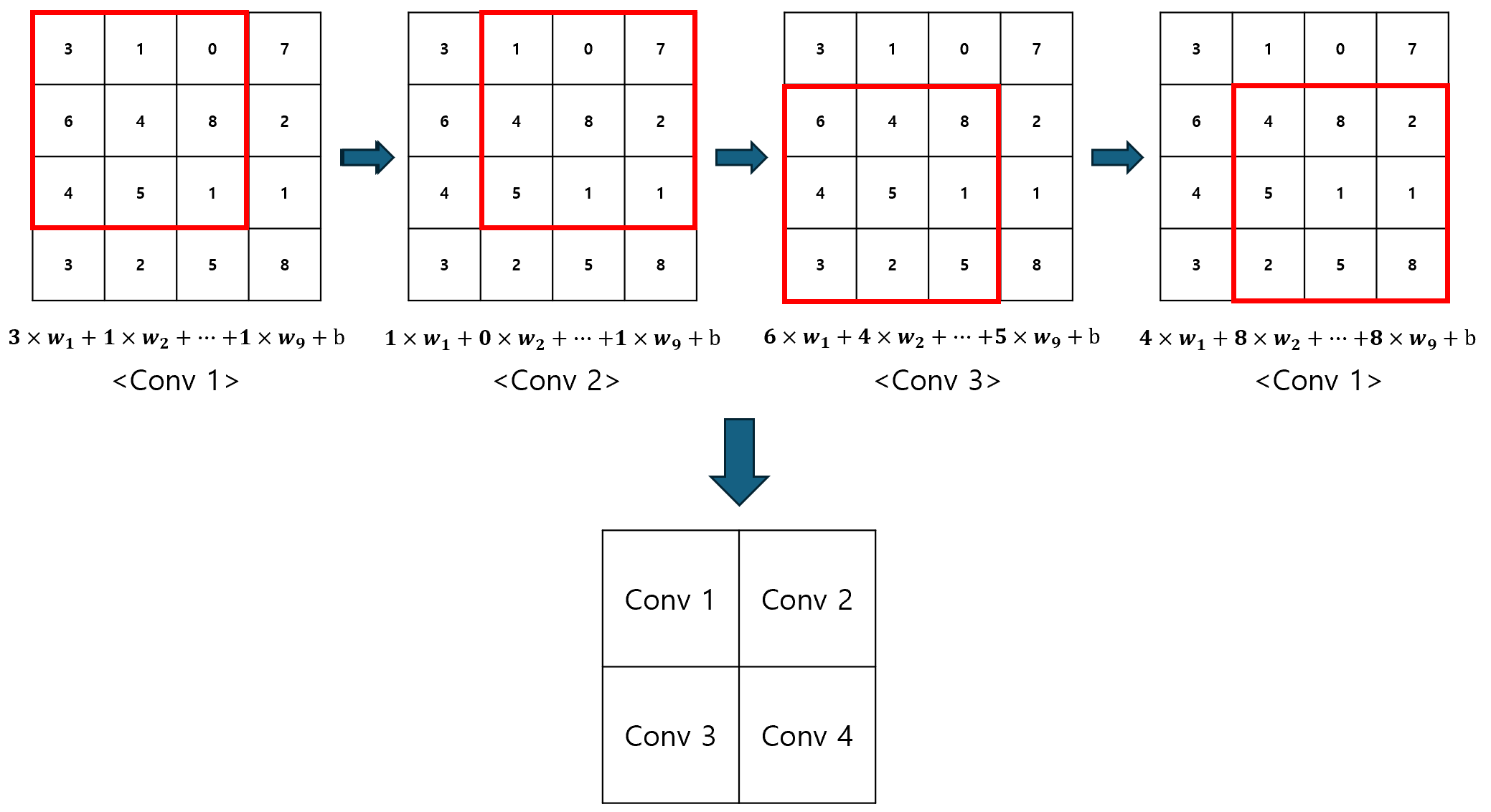
밀집층에서도 여러 개의 뉴런이 사용되듯, Convolution Layer에서도 여러 개의 뉴런(필터)이 사용될 수 있다. 당연히 각 필터마다 가중치가 다르기 때문에, 이 때의 특성 맵은 3차원 데이터가 될 것이다.
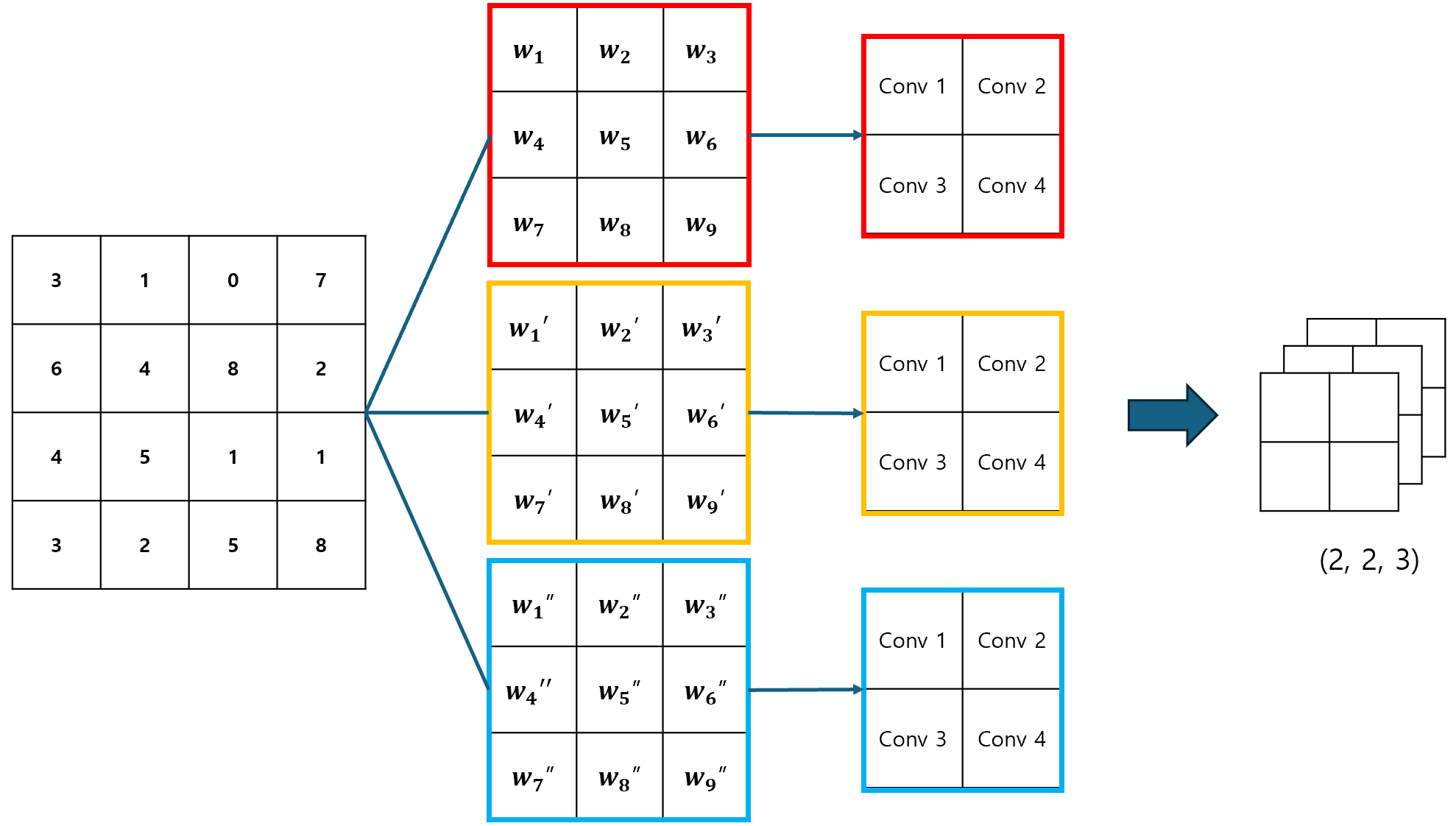
CNN은 2차원 데이터를 그대로 활용할 수 있으며, 입력 데이터의 크기보다 훨씬 작은 크기의 필터를 사용할 수 있기 때문에, 이미지 처리 분야에서 매우 뛰어난 성능을 자랑한다.
2. Convolutoin Layer
Convolutoin Layer를 구성하기에 앞서, 알아두어야 할 몇 가지 개념들에 대해 살펴보기로 하자.
1) Conv2D 클래스
2차원 입력을 처리하는 Convolutoin Layer를 만들기 위해, keras.layers의 Conv2D 클래스를 이용할 수 있다. Conv2D 클래스를 이용해 Convolutoin Layer를 만들 때에는 필터의 개수, 커널의 크기, 활성화 함수를 지정해주어야 한다.
from tensorflow import keras
kersa.layers.Conv2D(10, kernel_size=(3, 3), activation='relu')참고로, CNN이라고 해서 Convolutoin Layer로만 구성되어 있는 것은 아니며, 1개 이상의 Convolutoin Layer를 포함하는 신경망은 모두 CNN이라 부른다.
2) Padding과 Stride
먼저 Padding이란, 2차원 입력 데이터의 주변을 0으로 채우는 것을 말한다.
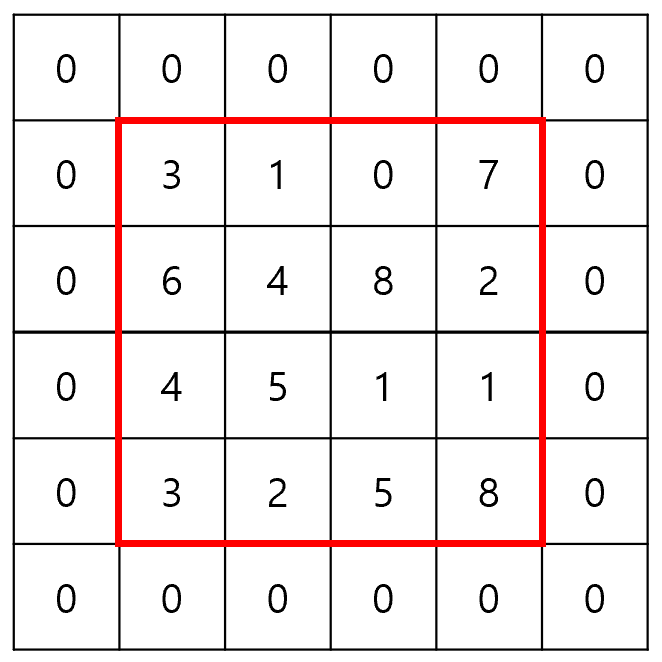
위에서 살펴보았듯이 Convolution을 수행하고나면, 특성 맵은 입력 데이터보다 작은 크기로 압축된다. 하지만, 상황에 따라 특성 맵의 크기가 입력 데이터와 동일해야 할 수도 있는데, 이 때 사용할 수 있는 방법이 Padding이다.
예를 들어, (4, 4) 크기의 입력에 (3, 3) 크기의 커널을 적용하여 (4, 4) 크기의 특성 맵을 만들어야 하는 상황을 생각해보자. 이 때, Padding을 활용하여 입력 데이터를 (6, 6) 크기로 조작하면, (4, 4) 크기의 특성 맵을 만드는 것이 가능해진다.
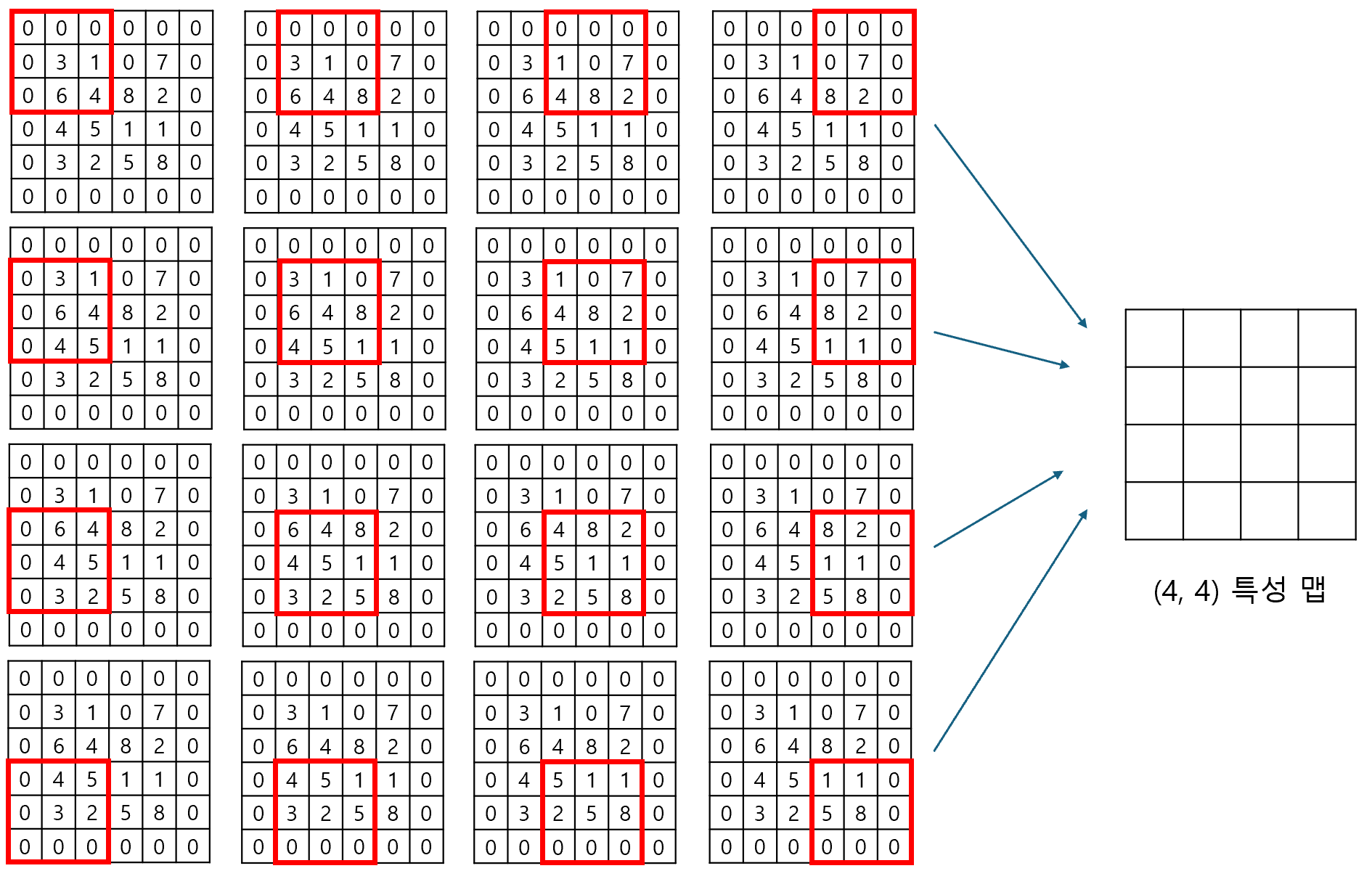
0으로 Padding 하였기 때문에, 슬라이딩 윈도우의 횟수만 증가했을 뿐 실제 연산 결과는 동일하다. 이러한 이유에서 Zero-Padding을 다른 말로, Same Padding이라고도 부른다. 이와 반대로 Padding을 적용하지 않은 순수한 입력 데이터는 Valid Padding이라고 부른다.
Padding이 필요한 또 하나의 이유는, 입력 데이터를 Convolution 연산에 공평하게 참여시키기 위함이다. 아래의 그림을 보자. 모퉁이에 위치한 데이터는 한번만 연산에 참여하는 반면, 중앙에 위치한 데이터는 모든 연산에 참여하게 된다.
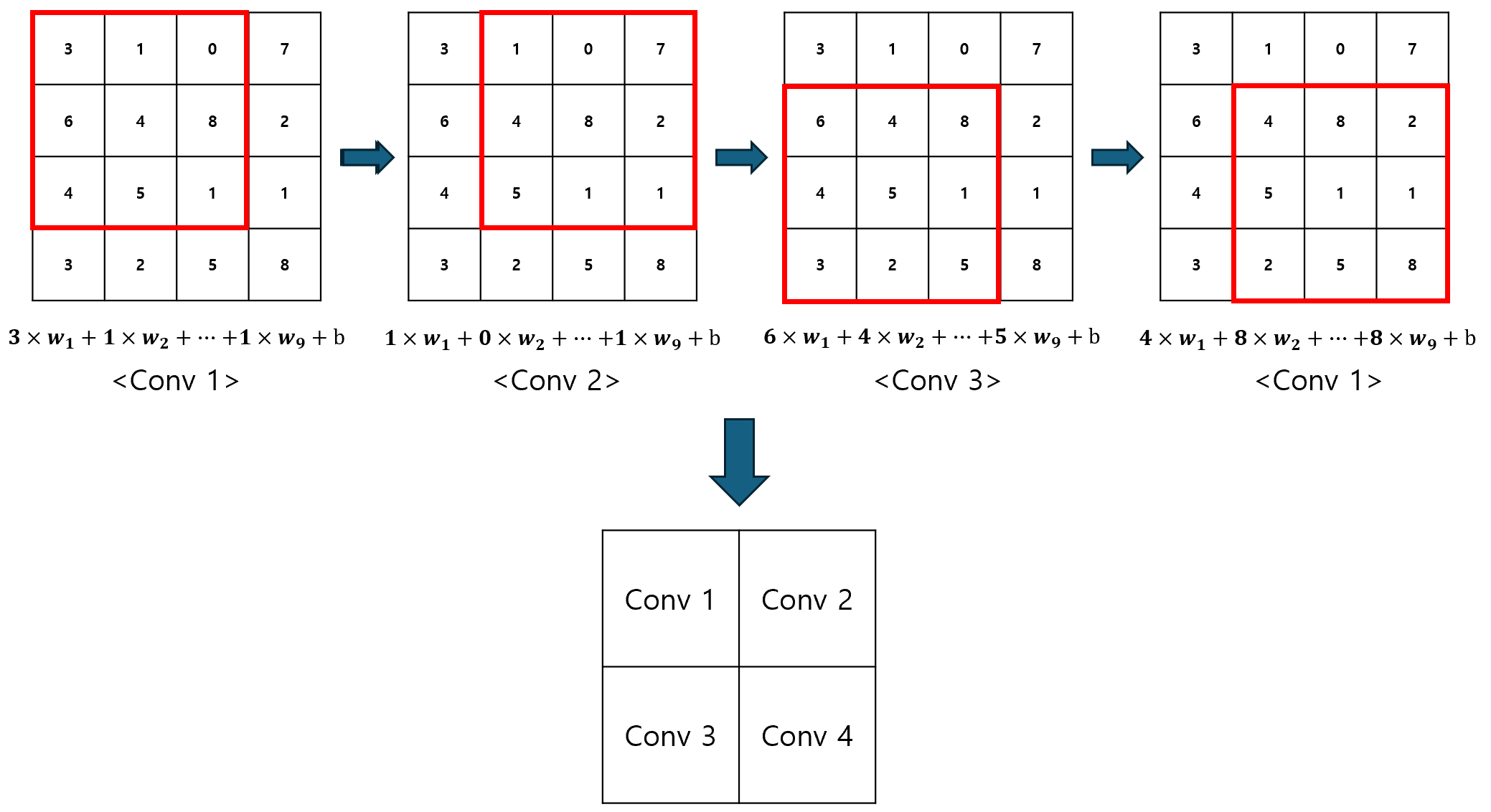
즉, 모퉁이에 있는 데이터는 출력에 주는 영향이 약화되고, 중앙에 있는 데이터는 출력에 주는 영향이 강화되는 것이다. 이 때, Padding을 적용하면, 이와 같은 불균형이 완화된다.

Padding을 적용하고나니, 모퉁이에 있는 원소는 4번, 중앙에 있는 원소는 9번 연산에 참여하게 되었다. Padding 적용 전에는 참여율이 4배 차이났던 것과 비교하면, 확실히 완화된 모습이다. Conv2D 클래스에서 Padding을 사용하려면, padding 매개변수를 same으로 지정해주면 된다.
kersa.layers.Conv2D(10, kernel_size=(3, 3), activation='relu', padding='same')다음으로, Stride는 필터를 한번에 얼마만큼 이동시킬지를 나타내는 값이다. 지금까지는 필터를 1칸씩만 이동시켰지만, 상황에 따라 2칸씩 이동시키는 것도 가능하다. 단, Stride의 크기가 커지면, 그만큼 특성 맵의 크기는 점점 작아지게 된다. Stride를 지정할 때에는 strides 매개변수를 이용하면 된다.
kersa.layers.Conv2D(10, kernel_size=(3, 3), activation='relu', padding='same', strides=1)Stride의 값은 주로 1을 사용하는데, strides 매개변수의 기본 값이 1이므로, 사실상 strides 매개변수를 사용할 일은 거의 없다.
3) Pooling
Convolutoin Layer에서 만들어진 특성 맵의 가로와 세로 크기를 줄이는 것을 Pooling이라 한다(특성 맵의 개수는 줄어들지 않는다). 특성 맵의 크기가 줄어든다는 점은 Stride를 조절하는 것과 동일하지만, Pooling을 사용하는 방식의 성능이 더 좋은 것으로 알려져있다.
예를 들어, (2, 2, 3) 크기의 특성 맵에 Pooling을 적용하면, (1, 1, 3) 크기의 특성 맵으로 변환된다.
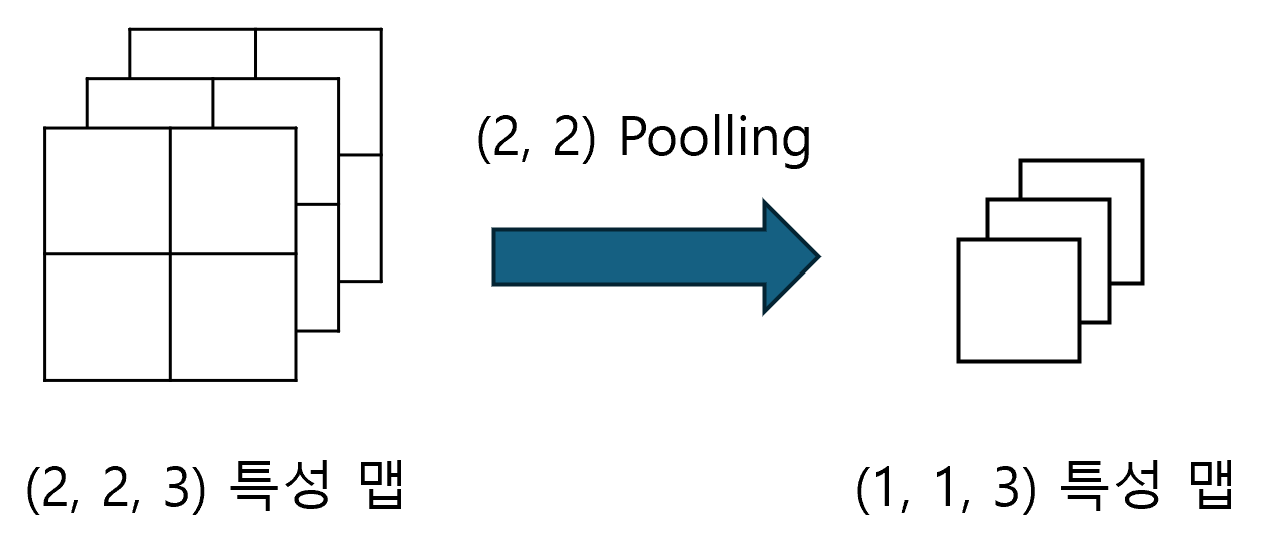
Pooling도 마치 Convolution 처럼 슬라이딩 윈도우 방식으로 동작하면서, 윈도우 내의 최대 값 또는 평균 값을 계산한다. 이를 각각 Max Pooling(최대 풀링)과 Average Pooling(평균 풀링)이라 하는데, Average Pooling의 경우 중요한 정보를 희석시킬 수 있다는 위험성 때문에, 자주 사용되지는 않는다.
Pooling의 가장 큰 특징은 윈도우가 겹치지 않도록 이동한다는 것이다. 예를 들어 Poolong의 크기가 (2, 2)일 경우, 가로 세로로 두 칸씩 이동하게 된다. 즉, Stride가 2가 되는 것이다.
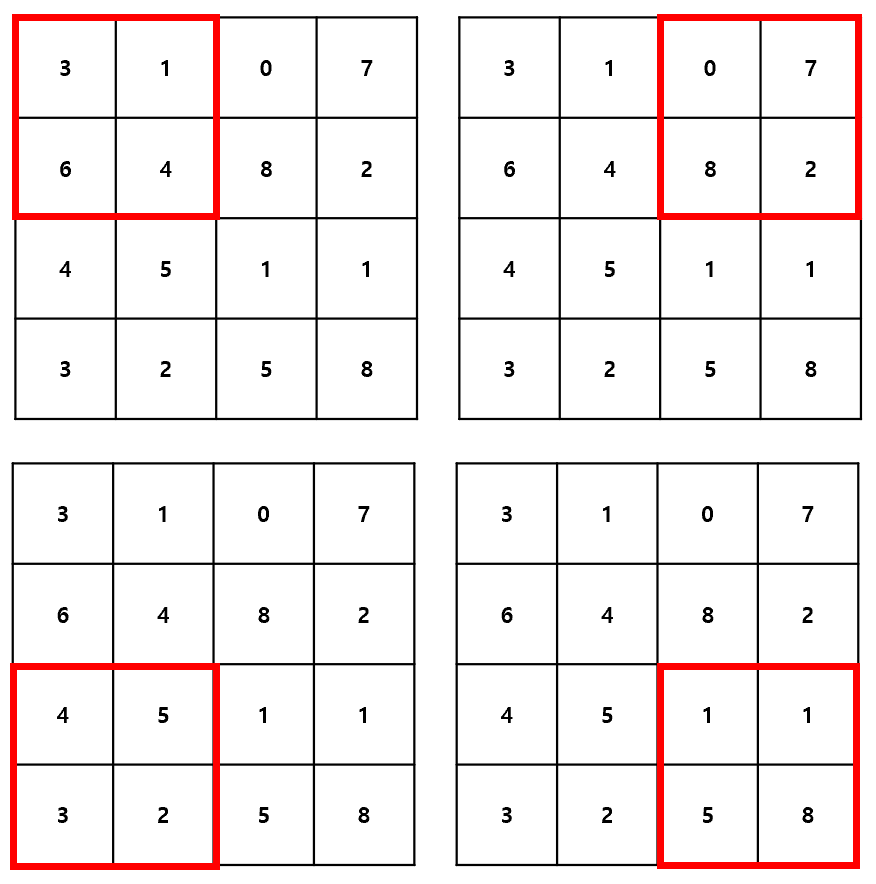
Pooling Layer는 Convolution Layer와 함께 사용되지만, Convolution Layer와 구별되는 별개의 Layer이다. Keras에서는 MaxPooling2D 클래스와 AveragePooling2D 클래스를 통해 Pooling 기능을 제공하고 있다.
keras.layers.MaxPooling2D(2)
keras.layers.AveragePooling2D(2)Pooling의 크기만 지정해주면, Stride의 크기는 자동으로 Pooling의 크기와 동일하게 설정된다.
3. 컬러 이미지에서의 Convolution
컬러 이미지는 RGB의 세가지 색상으로 표현되기 때문에, 3차원 배열로 표시된다. 물론, 3차원 배열에서도 Convolution 연산이 가능하다. 그저 필터를 3차원으로 구성하기만 하면 된다. 이 때, 하나의 필터에 대응되는 특성 맵의 차원은 필터의 차원과 무관하게 항상 2차원이다.
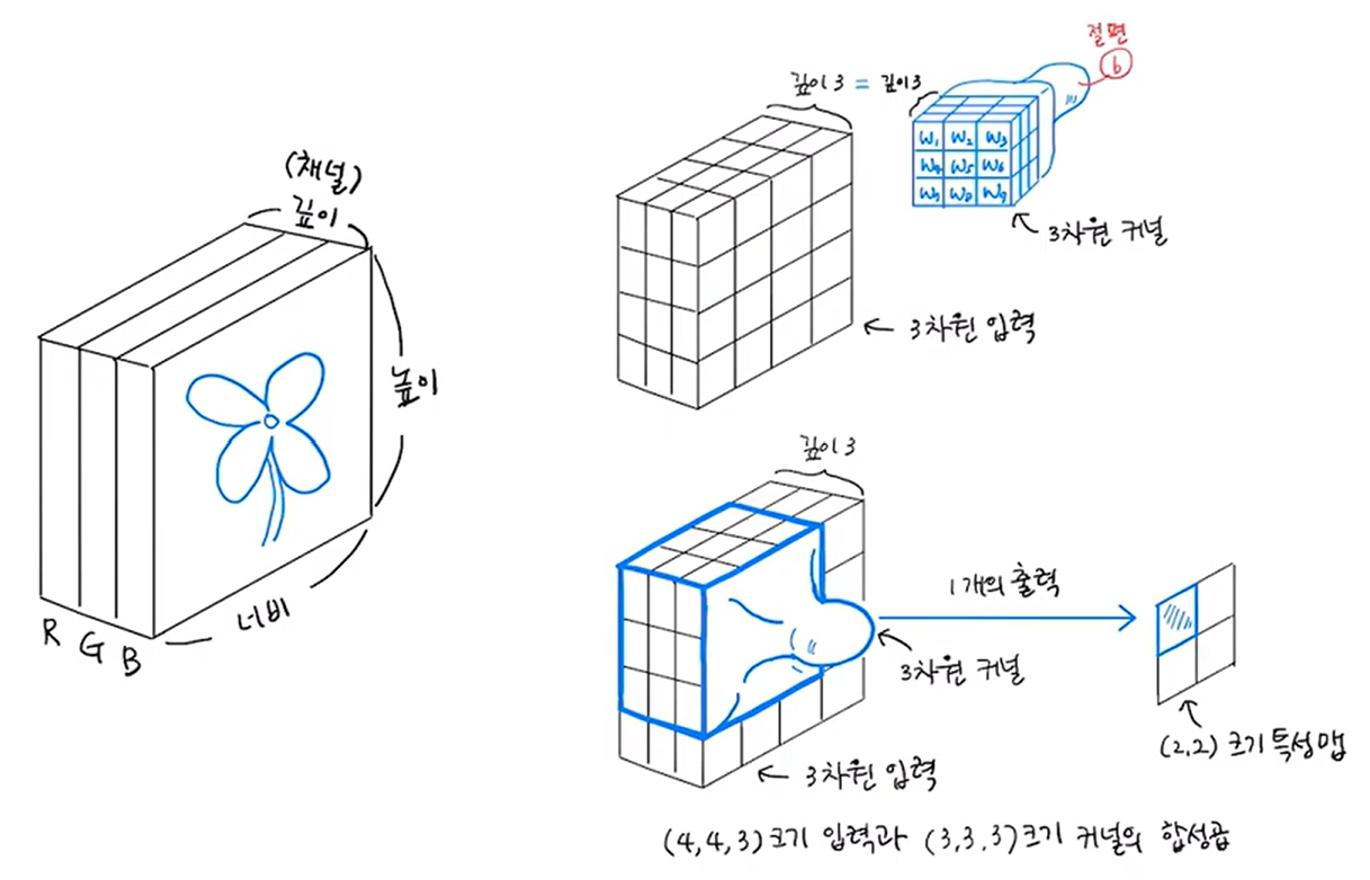
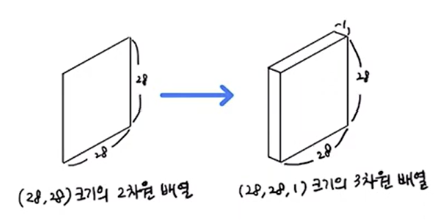
사실 Keras의 Convolution Layer는 항상 3차원 입력을 기대한다. 따라서, 흑백 이지미를 사용해야 하는 경우 2차원 배열을 3차원 배열로 변환하여 전달해야 한다.
CNN은 깊이가 깊어질수록, 특성 맵의 가로 세로 길이는 줄어들고, 개수는 늘어나는 형태를 갖는다. 이러한 형태 덕분에 CNN은 처음에는 대략적인 특징에만 집중하다가, 층이 깊어질수록 구체적인 특징에 집중하게 된다. 이렇게 해서 만들어진 최종 특성 맵은 출력층 이전에 있는 마지막 밀집층에서 1차원으로 펼쳐져, 밀집층의 입력 값으로 사용된다.
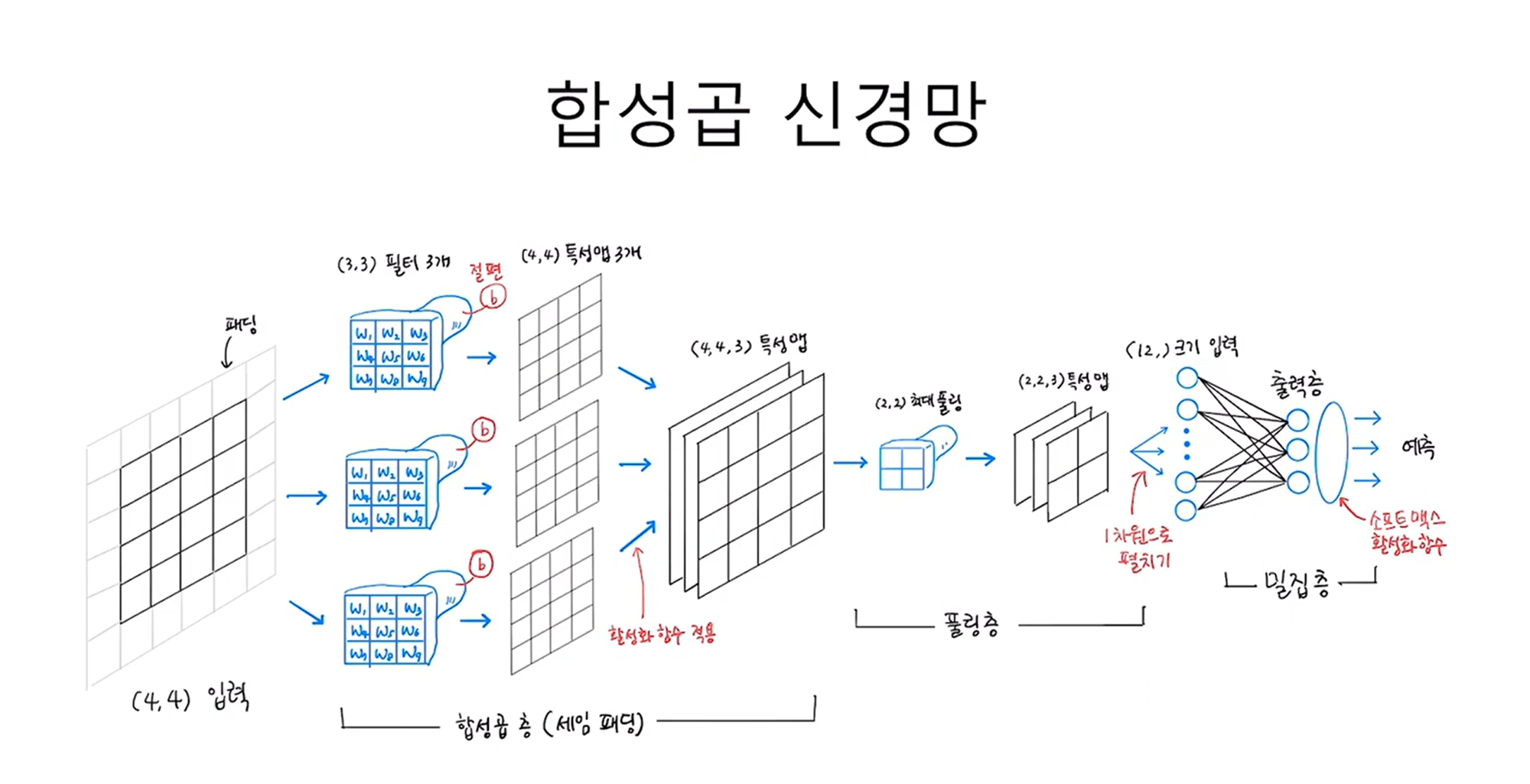
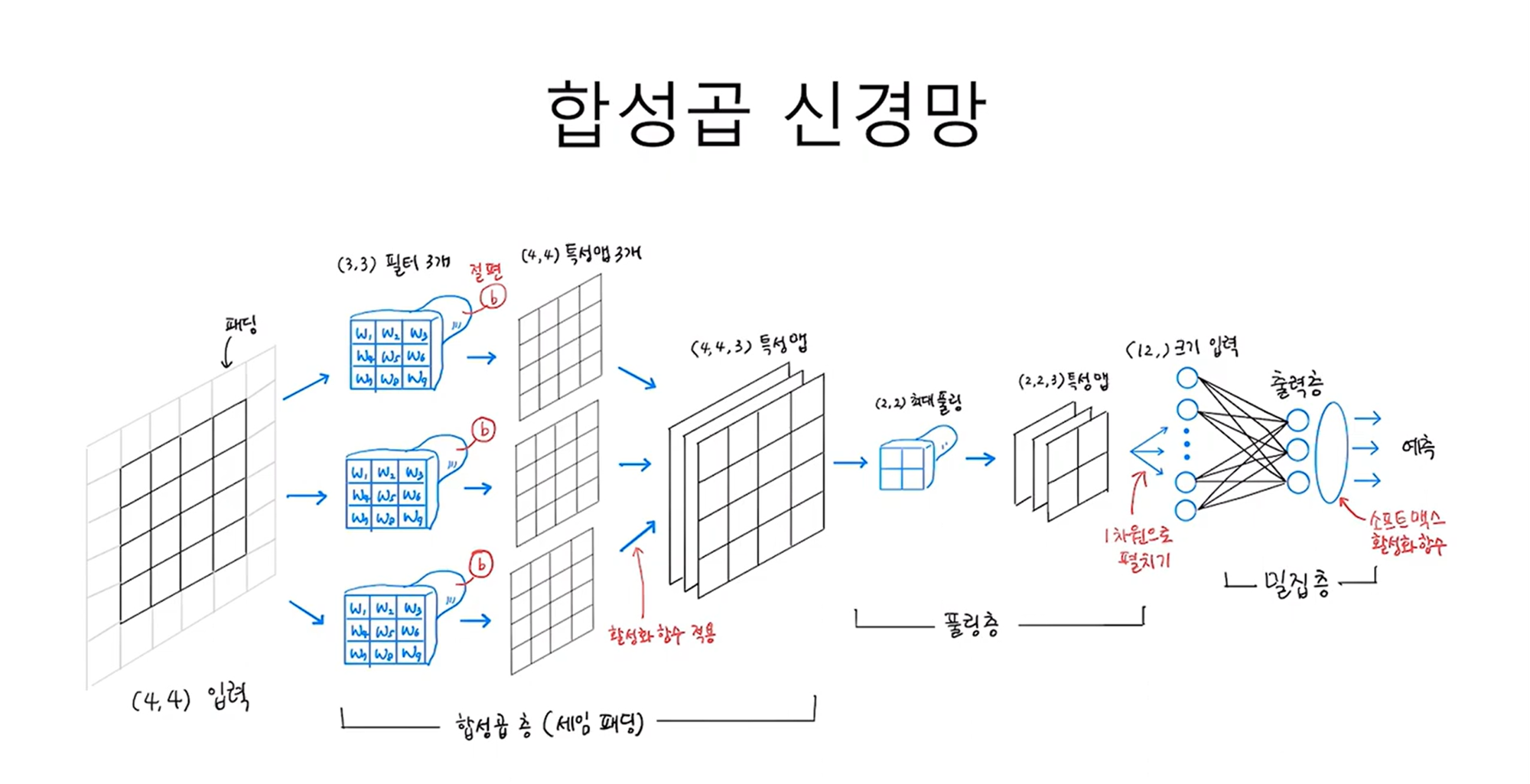
지금까지 살펴본 CNN의 전체 구조를 그림으로 나타내면 아래와 같다.