머신러닝이란
알고리즘
수학과 컴퓨터 과학, 언어학 또는 관련 분야에서 어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것, 계산을 실행하기 위한 단계적 절차
머신러닝은 크게 3가지로 분류.
- Supervised Learning(지도 학습)
= 정답을 알려주면서 학습시키는 방법 (ex. 회귀, 분류) - Unsupervised Learning(비지도 학습)
= 정답을 알려주지 않고 Clustering(군집화) 하는 방법 (ex. 군집, 시각화와 차원 축소, 연관규칙 학습) - Reinforcement Learning(강화 학습)
= 주어진 데이터없이 실행과 오류를 반복하면서 학습하는 방법이며 알파고 탄생시킨 방법
= 강화학습의 개념은 Agent(에이전트), Enviroment(환경), State(상태), Action(행동), Reward(보상)
머신러닝의 Regression(회귀)와 Classification(분류)
Regression
모든 문제를 풀기 위해서는 먼저 입력값(input)과 출력값(output)을 정의해야한다.
Q. 사람의 얼굴 사진을 보고 몇 살인지 예측하는 문제
- 입력값은 '얼굴 사진' 이 되고 출력값은 '예측한 나이'가 된다.
- 나이의 값은 연속적이다.(ex.1살 ,2살, 3살 ,15살, 33.3살, 90살)
- 이런 식으로 출력값이 연속적인 소수점으로 예측하게 하도록 푸는 방법을 회귀
+예측하고 싶은 종속변수가 숫자일 때 회귀라는 머신러닝의 방법을 사용
ex) 독립변수: 온도 / 종속변수: 레몬에이드 판매량 / 학습시킬 데이터 만드는 법: 온도와 그날 판매량 기록
(source:https://opentutorials.org/)
Classification
Q. 대학교 시험 전 날 공부한 시간을 가지고 해당 과목의 이수 여부(P or F)를 예측하는 문제
- 이 문제에서 입력값은 '공부한 시간' 그리고 출력값은 '이수여부'가 된다.
- 우리는 이수 여부를 0,1 이라는 이진 클래스로 나눌 수 있다.
- 0이면 미이수(Fail), 1이면 이수(Pass)
- 위와 같은 경우를 Binary classification(이진분류) 이라고 부른다.
Q. 대학교 시험 전 날 공부한 시간을 가지고 해당 과목의 성적(A,B,C,D,F)을 예측하는 문제
- 이 문제는 입력값은 '공부한 시간' 그리고 출력값은 5개의 클래스(A,B,C,D,F) 이다.
- 이와 같은 방법을 Multi-class classification, Multi-label classification(다중 분류) 이라고 부른다.
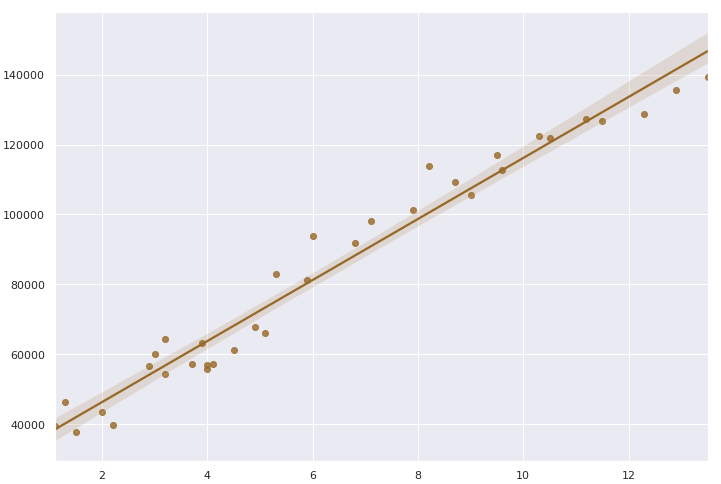
선형회귀(Linear Regression)
두 데이터 간의 직선 관계를 찾아내서 x값이 주어졌을 때 y값을 예측하는 것.
컴퓨터가 풀 수 있는 문제 중에 가장 간단한 것이 선형회귀.
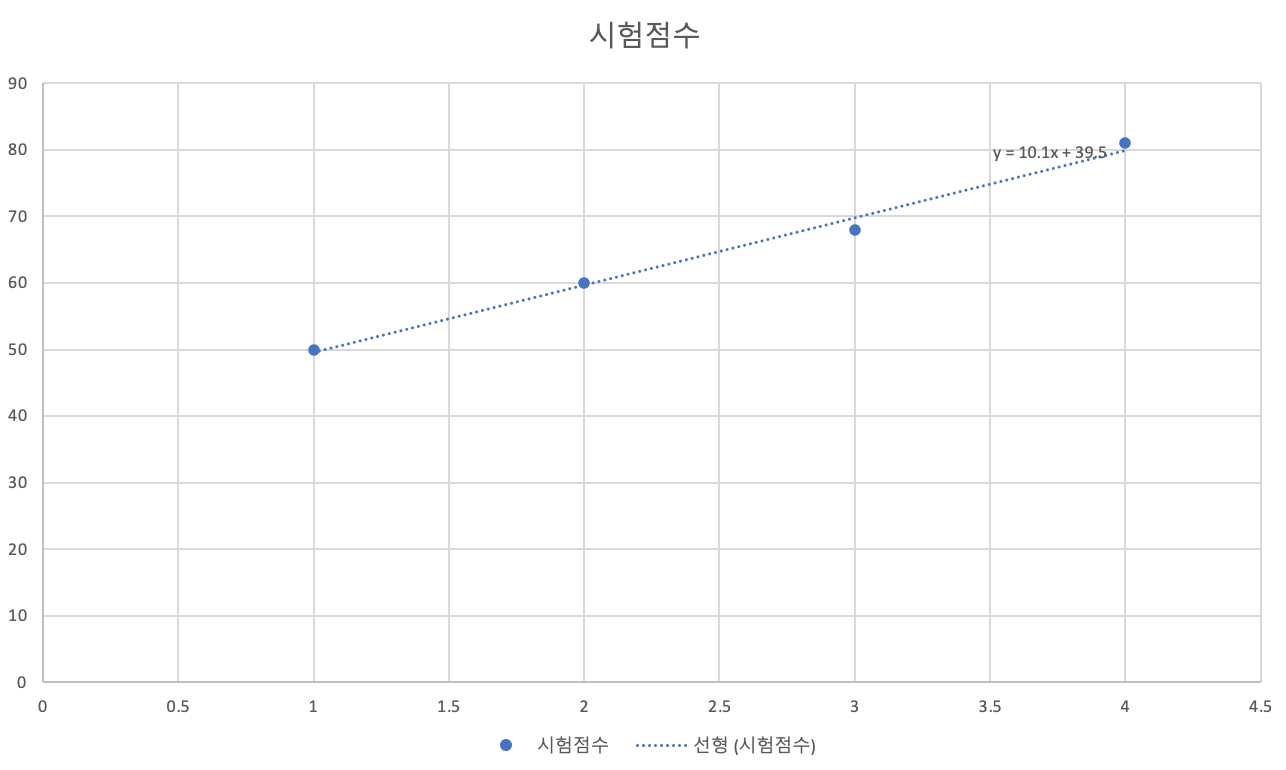
시험 점수를 예측하기 위해 우리가 만든 임의 직선을 Hypothesis(가설)
H(x) = Wx + b
우리는 정확한 시험 점수를 예측하기 위해 가설과 정답의 거리가 가까워지도록 해야한다.
= Loss function or Cost(손실 함수)
y는 정답 값이라고 했을 때 H(x)와 y의 거리가 최소가 되어야 이 모델이 잘 학습된 것.
= 손실함수가 낮아야 모델이 잘 학습된 것
경사하강법
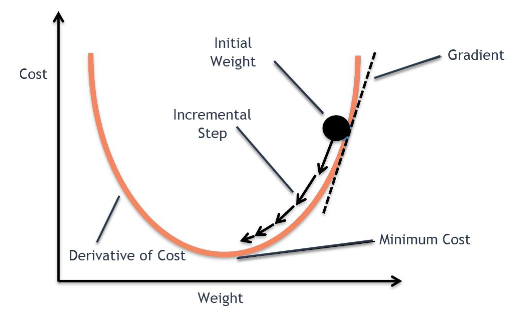
- 우리의 목표는 손실 함수를 최소화 하는 것.
- 경사 하강법을 써서 점진적으로 문제를 해결.
- 한칸씩 전진하는 단위를 Learning rate(lr)
Learning rate
우리가 만든 머신러닝 모델이 잘 학습할려면 적당한 Learning rate를 찾는 것이 필수적.
Learning rate가 작으면 최소값을 찾는데 많은 시간이 걸림
Learning rate가 크면 찾으려는 최소값을 지나치게 될 수 있고, Overshooting 할 수 있음.
우리의 목표는 이 손실 함수의 최소점인 Global cost minimum을 찾는 것
그런데 Learning rate를 잘못 설정할 경우 Local cost minimum에 빠질 가능성이 높음
Cost가 높다는 얘기는 우리가 만든 모델의 정확도가 낮다는 말
따라서 우리는 최대한 Global minimum을 찾기 위해 좋은 가설과 좋은 손실 함수를 만들어서
기계가 잘 학습할 수 있도록 만들어야하고 그것이 바로 머신러닝 엔지니어의 핵심 역할
논리회귀(Logisic regression, Sigmoid function)
선형회귀로 풀기 어려운 문제들로 인해 논리회귀 등장
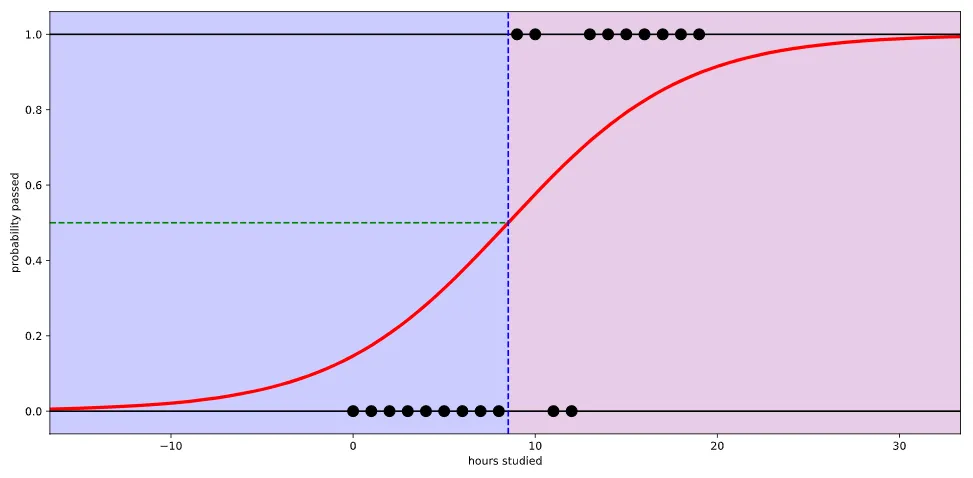
선형회귀에서의 가설은 H(x) = Wx + b
논리회귀에서는 Sigmoid 함수에 선형 회귀식을 넣어준다.
Crossentropy
= 논리회귀에선 임의의 입력값에 대해 우리가 원하는 확률 분포 그래프를 만들도록 학습시키는 손실함수
(Keras에서 이진 논리 회귀의 경우 binary_crossentropy 사용)
(Keras에서 다항 논리 회귀의 경우 categorical_crossentropy 사용)
One-hot encoding
Multi-label classification(다항 분류) 문제를 풀 때 출력값의 형태를 0과 1로만으로 표현
1. 클래스(라벨)의 개수만큼 배열을 0으로 채운다
2. 각 클래스의 인덱스 위치를 정한다
3. 각 클래스에 해당하는 인덱스에 1을 넣는다
Softmax 함수
- Softmax는 선형 모델에서 나온 결과(Logit) 를 모두 더하면 1이 되도록 만들어주는 함수
- 다 더하면 1이 되도록 만드는 이유는 예측의 결과를 Confidence(확률)로 표현하기 위함
- One-hot encoding을 할 때도 라벨의 값을 전부 더하면 1(100%)가 되기 때문
Preprocessing(전처리)
- 넓은 범위의 데이터 정제 작업
- 필요없는 데이터를 지우고 필요한 데이터만을 취하는 것
- null 값이 있는 행을 삭제하는 것
- Normalization(정규화), Standardization(표준화) 등의 작업 포함
- Normalization(정규화)
= 데이터를 0과 1사이의 범위를 가지도록 만듬
= 같은 특성의 데이터 중에서 가장 작은 값을 0으로 만들고, 가장 큰 값을 1로 만듬
ex) 100점 만점 시험 실제점수:50 / 정규화 점수: 0.5 500점 만점 시험 실제점수: 50 / 정규화 점수: 0.1
Standardization(표준화)
= 데이터의 분포를 정규분포로 바꿔줌
= 즉 데이터의 평균이 0이 되도록 하고 표준편차가 1이 되도록 만들어줌
= 데이터의 평균을 0으로 만들어주면 데이터의 중심이 0에 맞춰지게 된다
= 표준편차를 1로 만들어주면 데이터가 예쁘게 Normalized 된다
= 일반적으로 학습속도(최저점 수렴 속도)가 빠르고, local mimima에 빠질 가능성 적음
Deep Learning, Deep Neural Networks, MLP (딥러닝)
= 선형회귀 사이에 비선형의 무언가를 넣는 층을 쌓아서 사용하는 모델
Deep Neural Networks 구성방법
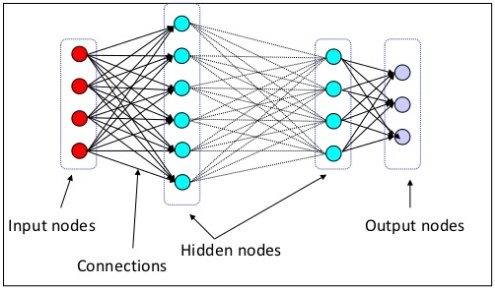
- Input layer(입력층) : 네트워크의 입력 부분으로 학습시키고 싶은 x값
- Output layer(출력층) : 네트워크의 출력 부분으로 우리가 예측한 값인 y값
- Hidden layers(은닉층) : 입력층과 출력층을 제외한 중간층
기본적인 뉴럴 네트워크에서는 보통 은닉층에 중간 부분을 넢게 만드는 경우가 많음
ex) 입력층 노드 개수 4개 / 첫번째 은닉층 노드 개수 8개 / 두번째 은닉층 노드 개수 16개 /
세번째 은닉층 노드 개수 8개 / 출력층 노드 개수 3개
네트워크의 Width(너비)
= 은닉층의 개수를 그대로 두고 은닉층의 노드 개수를 늘리는 방법
네트워크의 Depth(깊이)
= 네트워크의 은닉층의 개수를 늘리는 방법
batch size, iteration, epoch
batch
= 데이터셋을 작은 단위로 쪼개서 학습을 시키는데, 데이터셋을 쪼개는 단위
ex) 1,000만개의 데이터셋을 1,000개 씩 쪼개어 10,000번 반복 batch size=1000 , ilteration = 10,000
epoch
batch를 몇 개로 나눠놓았냐에 상관없이 전체 데이터셋을 한 번 돌때 1 epoch이 끝남
Activaion functions (활성화 함수)
수많은 뉴런들은 서로 서로 빠짐없이 연결되어 있다.
뉴런들은 전기 신호의 크기가 특정 임계치를 넘어야만 다음 뉴런으로 신호를 전달하도록 설계되어 있다. 연구자들은 뉴런의 신호전달 체계를 흉내내는 함수를 수학적으로 만들었는데,
전기 신호의 임계치를 넘어야 다음 뉴런이 활성화 한다고해서 활성화 함수라고 부른다.
활성화 함수는 비선형 함수여야하며, 비선형 함수의 대표적인 예는 Sigmoid 함수이다.
따라서 비선형 함수 자리에 Sigmoid 함수를 넣으면 다음과 같다.
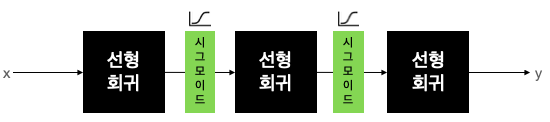
딥러닝에서 가장 많이 보편적으로 쓰이는 활성화함수는 ReLu이다.
다른 활성화 함수에 비해 학습이 빠르고, 연산 비용이 적고, 구현이 간단하다.
Overfitting, Underfitting
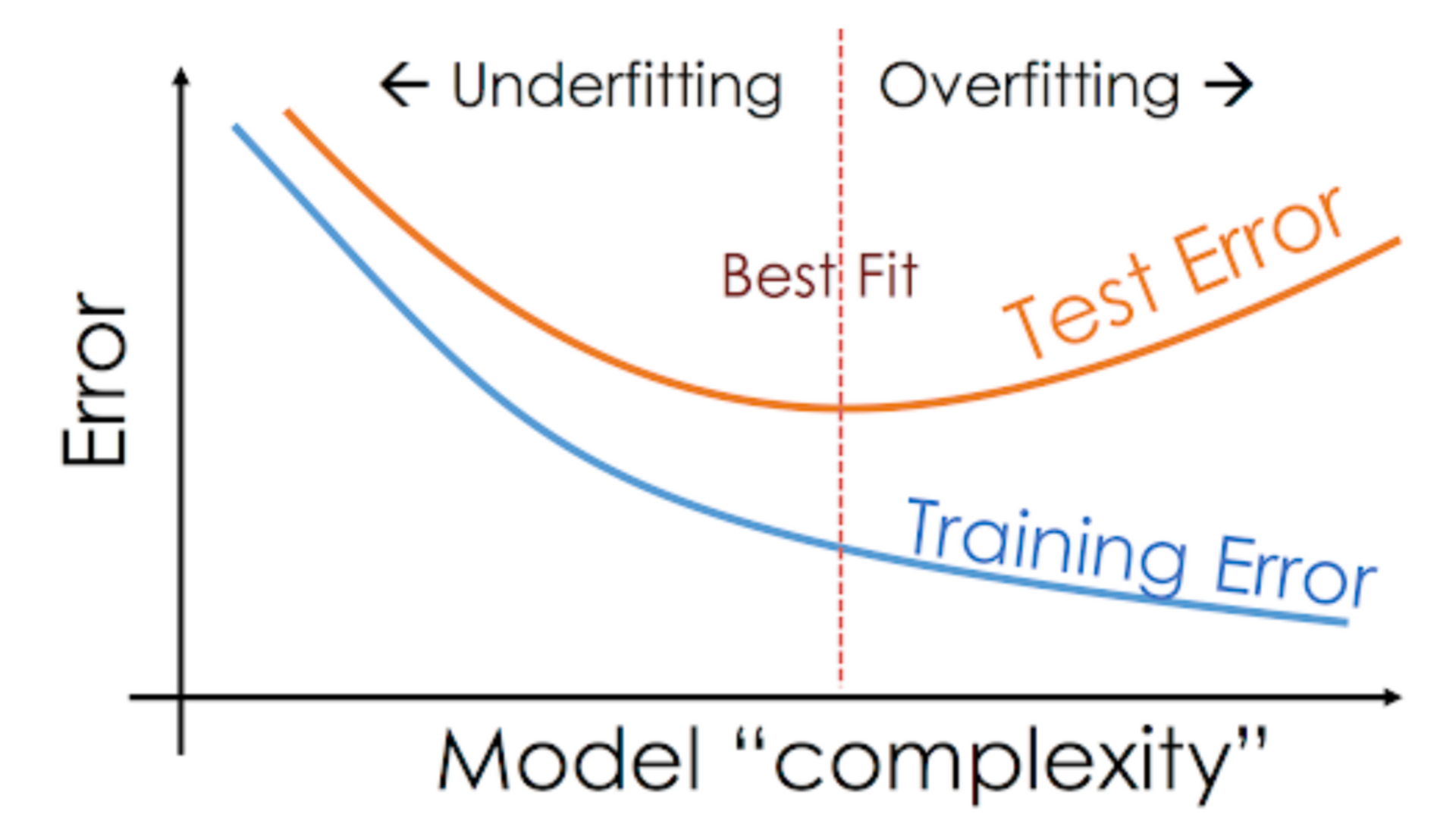
Overfitting(과적합)
딥러닝 모델을 설계/튜징하고 학습시키다 보면 가끔씩 Training loss는 점점 낮아지는데 Validation loss가 높아지는 시점이 있는데 이런 현상을 과적합 현상이라고 한다.
풀어야 할 문제의 난이도에 비해 모델의 복잡도가 클 경우 가장 많이 발생
Underfitting(과소적합)
반대로 풀어야할 문제의 난이도에 비해 모델의 복잡도가 낮을 경우 문제를 제대로 풀지 못하는 현상
- 딥러닝 모델을 학습시키다보면 과소적합보다는 과적합이 더 많이 발생
- 과적합을 해결하는 방법에는 대표적으로 데이터를 더 모으기, Data augmenation, Dropout
데이터셋 분할
- Training set
= 학습 데이터셋. 머신러닝 모델을 학습시키는 용도. 전체 데이터셋의 약 80% - Validation set
= 검증 데이터셋. 머신러닝 모델의 성능을 검증하고 튜닝하는 지표의 용도로 사용
= 모델에게 데이터를 직접 보여주진 않으므로 모델 성능에 영향을 미치지 않음
= 손실 함수, optimizer 등을 바꾸면서 모델을 검증하는 용도로 사용 - Test set
= 정답 라벨이 없는 실제 환경에서의 평가 데이터셋
라이브러리
from tensorflow.keras.models import Sequential = 모델을 정의할 때 쓰는 클래스
from tensorflow.keras.models import Dense = 가설을 구현할 때 사용
import pandas as pd = csv 파일을 읽을 때 사용
import matplotlib = 그래프를 그릴 때 사용
import seeborn as sns = 그래프를 그릴 때 사용
from sklearn.model_selection import train_test_split = 머신러닝 돕는 패키지. 트레이닝셋, 테스트셋 분류