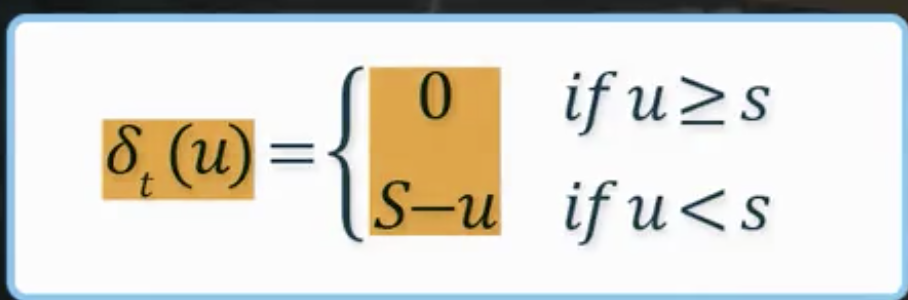고려대학교 산업공학과 정태수 교수님 강의 정리

Week5: 마르코브 결정 프로세스-1

• Lecture

5-1. MDP 개요

MDP

구분

• Deterministic DP: 정해진 상태로만 전이
• Stochastic DP: 상태가 확률적으로 결정

정의

1. 일종의 확률과정
2. 의사결정자가 확률과정을 관찰하고 행동을 선택함으로써 이후 프로세스에 영향을 미침
   --> 의사결정자는 추계적 과정 상의 상태와 선택한 행동에 따른 일련의 (양 혹은 음의) 보상을 얻게 됨

MDP의 구성요소

Timespace

상태

행동

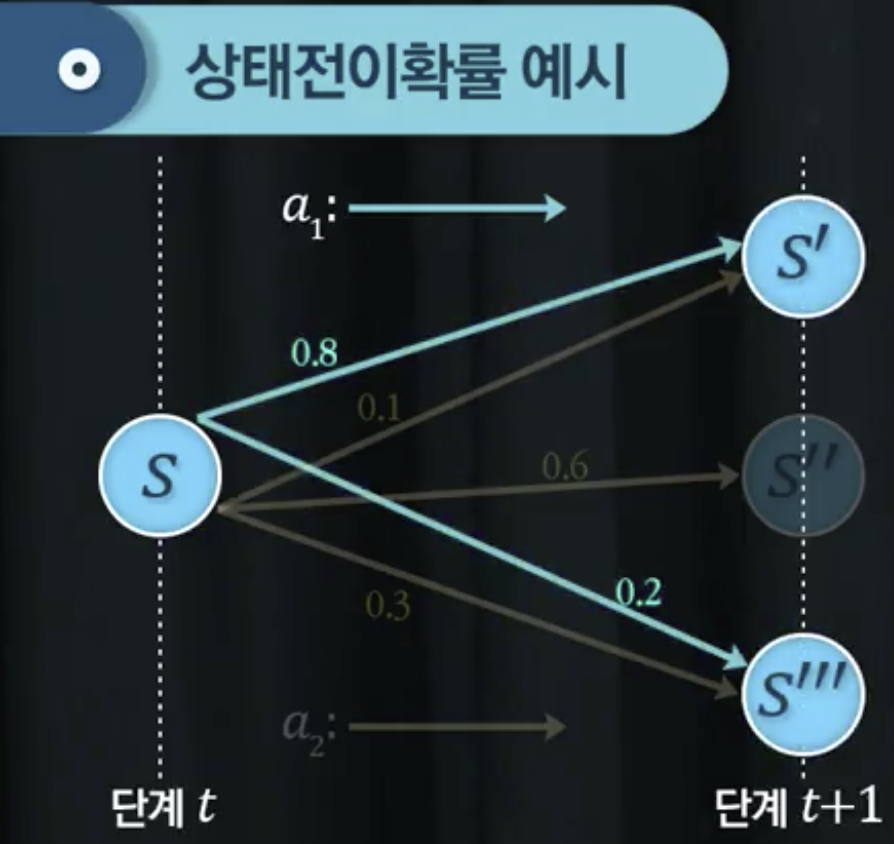
상태전이확률

보상

감가율

MDP 정책

MDP를 통해서 얻고자 하는 것

• 매 단계마다 어떤 상태에서 어떤 행동을 해야 내가 원하는 결과(보상합 최대화)를 얻을 것인가?
  --> 각 단계별로 어떤 상태에서는 어떤 행동을 취해야하는지 규칙을 찾아내는 것

의사결정규칙

• History-dependent: 과거의 모든 이력을 입력받아 다음 행동을 출력하는 함수
• Markovian: 현재 상태만으로 다음 행동을 출력하는 함수
• Deterministic: 어떤 행동을 확정하여 함수형식으로 주어짐
• Probabilistic: 어떤 행동을 확률적으로 제시함
  
  

정책

5-2. MDP 예시

MDP 예시1 (주사위 던지기 게임)

게임 규칙

MDP 정의

• Timespace: 매 라운드가 의사결정 시점의 집합이 됨
• State space: $S_t=\{in, end\}$
  • 게임을 진행 중인 상태: in
  • 게임이 종료된 상태: end
• Action space: 게임의 상태에 따라 행동이 다름
  • 게임을 진행 중인 상태 $A_{in}=\{go, stop\}$
  • 게임이 종료된 상태 $A_{end}=\{stop\}$
• 상태전이확률:
  • 이전 상태의 이력이 중요하지 않음 (현재 어느 상태에 있는지가 중요)
  • 다음 상태가 일어날 확률을 결정함
  • 모든 경우의 수가 나열되어야 함
    • $P_t(in|in,go) = 2/3$
    • $P_t(end|in,go) = 1/3$
    • $P_t(in|in,stop) = 0$
    • $P_t(end|in,stop) = 1$
    • $P_t(in|end,stop) = 0$
    • $P_t(end|end,stop) = 1$
• 보상: 어떤 상태에서 어떤 행동을 취했을 때 얻을 수 있는 기대값
  • $r_t(in, stop) = \$8$
  • $r_t(in, go) = \$4$
  • $r_t(end, stop) = \$0$

상태전이 다이어그램

MDP 예시2 (재고관리)

문제 설명 및 가정

기호

MDP 정의

• Timespace: 매달이 의사결정 시점의 집합이 됨
• 상태공간: 주문 전에 보유하고 있는 재고 수준 ($S=\{0,1,2, ... M\}$)
• 행동공간: 발주 전 재고수준과 창고용량을 고려한 주문량
  • 최대 (M-보유량) 만큼 발주 가능 ($A_s=\{0,1,2, ... M-s\}$)
• 상태전이확률
  
  
  
• 보상: 이익 (수익에서 비용을 밴 차분)
  • $r_t(s,a)=F(s+a)-O(a)-h(s+a)$
• 정책 예시: 매 단계별로 모든 상태에 대해서 내가 어떤 행동을 취해야 할 지 규정하는 함수