출처

• Charu C. Aggarwal (2021) 추천시스템 : 기초부터 실무까지 머신러닝 추천 시스템 교과서. 에이콘 출판사 59-107p
• Charu C. Aggarwal (2016). Recommendation System. Springer International Publishing 51-92p

2.1 Introduction

• Memory-based algorithm이라고도 불림
• 유사한 사용자들이 비슷한 평가 행동 패턴을 보이고, 비슷한 항목에 유사한 평가를 할 것이라고 가정

Neighborhood-based Algorithm 종류

2가지 계산 방식

• user-item 조합의 평가값 예측: $r_{uj}$ → 사용자 u에 대한 항목 j의 누락된 평가 예측
• top-k item or top-k user 결정
  • top-k item을 결정하는 것이 top-k user를 결정하는 것보다 일반적임
    • 웹 중심 시나리오에서 사용자에게 추천한 item 리스트를 보여주는데 사용되기 때문
  • 두가지 문제(top-k item/user)들은 서로 밀접한 관련이 있음
    • top-k item을 정하기 위해 해당 user에 대한 각 item의 평가를 예측해야됨
    • 효율성 개선 방법
      • 오프라인 단계에서 예측이 필요한 데이터를 미리 계산함
      • 계산된 데이터는 효율적인 방식으로 순위를 결정하는데 사용할 수 있음

2.2 Key properties of Ratings Matrices

• Specified entries: Training data
• Unspecified entries: Test data → Class variable or Dependent variable
  ⇒ 추천 문제는 분류/회귀 문제의 일반화로 볼 수 있음

평점 표현 종류

Long tail of rating frequencies

• item 간의 평가 분포는 Long-tail 속성이라고 불리는 속성을 만족함

  • 인기 상품의 평가만 빈번함

  • 대부분의 항목들은 드물게 평가됨

    

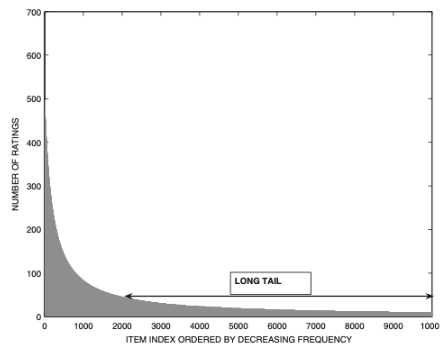
• 위 그래프로 부터의 중요한 시사점
  • 빈도가 낮은 상품을 판매자에게 추천하는 것이 유리
    • 고빈도 항목보다 저빈도 항목의 이익 마진이 큼 (경쟁이 덜 치열함)
    • Amazon과 같은 많은 회사들은 롱테일에 위치한 item을 판매하여 수익을 창출하고 있음
  • 롱테일에서 관측된 자료가 드물기 때문에, 평가를 예측하기가 더 어려움
    • 많은 추천 알고리즘들은 인기있는 항목을 추천하는 경향이 있음
      → 다양성에 부정적인 영향을 미침, 사용자에게 지루함을 느끼게 할 수 있음
  • 사용자가 자주 평가하는 항목의 수가 적다는 것을 알 수 있음
    • 이웃 기반 협업 필터링 알고리즘에 중요한 의미를 가짐 (이웃이 자주 평가하는 항목들을 기반으로 정의되기 때문)
    • 고빈도 상품은 저빈도 상품을 대표하지 않음
      → 본질적으로 평점 패턴에 다른 차이가 있음
      → 고빈도 상품으로 저빈도 상품을 예측할 경우, 추천 알고리즘에 대한 잘못된 결과를 초래할 수 있음

2.3 Predicting Ratings with Neighborhood-Based Methods

• Neighborhood: 예측을 위해 유사한 user or item을 찾아하 한다는 의미
• User-based / Item-based models
• Nearest Neighbors
  • Classification : row similarity로 결정됨
  • Collaborative filtering: rows or either columns를 기준으로 찾을 수 있음

2.3.1 User-based models

• 평점 예측이 계산되는 target user와 유사한 사용자를 찾기 위해 정의됨
  • target user의 이웃을 찾기 위해 다른 모든 user와의 유사도가 계산됨
• 유사도 함수(similarity function)가 필요
  • 사용자마다 평가 척도가 다를 수 있기 때문에 까다로움
• Pearson 상관계수 수식
  
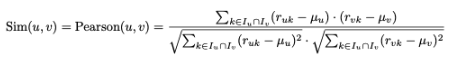
• 사용자의 평균 중심 평점 (mean-centered rating) → 스케일링
  
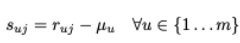
• 예측 평점 산출 수식
  
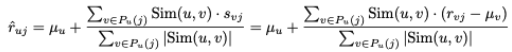
• 유사도 함수, 예측 함수, 피어 그룹 필터링은 다양한 방법으로 변형할 수 있다
• 롱테일의 영향: 실제 컨텍스트에서의 평점 분포는 Long-tail 분포를 따른다
  → 사용자 간의 차별 성이 적기 때문에 추천 품질을 악화시킬 수 있다!

예시

• User Rating matrices
  
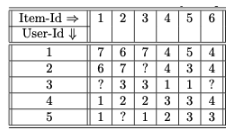
• 유사도 Sim(u,v) 계산
  • Cosine(1,3) = 0.956
  • Pearson(1,3) = 0.894 ✅
• 유사도 기반 가까운 사용자 선정
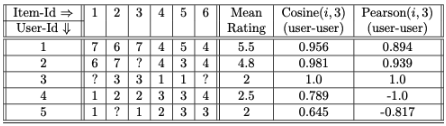
  • user3 기준, 1 / 2 선택
• 평균 중심 평점 계산
  
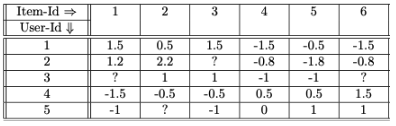
• 예측 평점 계산
  

2.3.2 Item-based models

• 피어그룹은 아이템으로 구성됨 → 아이템 간의 유사도가 계산되어야함!
• 피어슨 상관 관계보다 조정된 코사인 유사도가 일반적으로 더 우수한 결과를 보임

  • 조정된 코사인 유사도: 유사도 값을 계산하기 전에 평점이 mean-centered 이기 때문

    

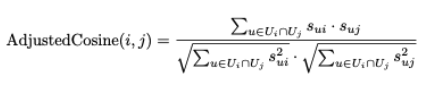
사용자 u의 아이템 t의 평점 결정 과정

1. 조정된 코사인 유사도를 기반으로 아이템 t와 가장 유사한 상위 k 아이템들을 결정 (여기서 예제의 k=2)

   • $Q_t(u)$ : 사용자 u가 평점을 지정한 아이템 t에 상위 k로 매칭되는 아이템들

   

   

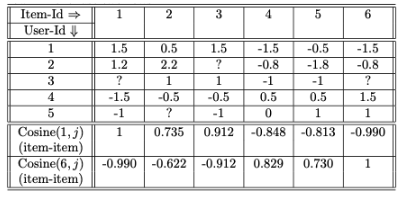
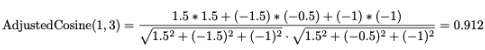
   • Item1: 2,3과 가장 유사
   • Item6: 4,5와 가장 유사

2. 이 평점들의 가중 평균 값을 예측 값이라고 함

   1. 평균의 아이템j의 가중치 = 아이템j와 타깃 아이템 t간의 조정된 코사인 유사도

   

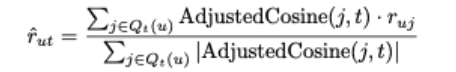
3. 유사한 항목에 대한 사용자 자신의 평점을 활용하는 것

   

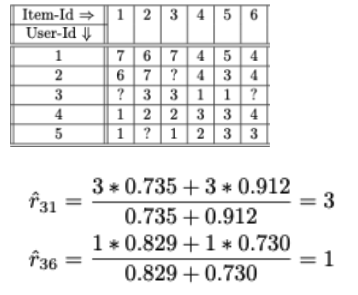
   $\therefore$ user 3에게는 아이템 1이 더 선호될 것

★ 2.3.3 효율적 구현 및 계산 복잡성

• 이웃 기반 방법론은 target user의 가장 적절한 추천 항목 or 사용자를 결정하는데 쓰인다
• 단도직입적인 방법 (straightforward approach)

  • 모든 user-item에 대해 가능한 평점을 모두 예측하고, 이들에 대해 순위를 매기는 것

  • user-item 조합에 대한 예측 과정이 중간 계산 과정에 재사용됨

    → 중간 계산을 저장하고 순위 과정에 사용하기 위해 “오프라인 단계 (offline phase)"를 사용하는 것이 좋음

• 오프라인 단계
  • 유사도 값(item-item or user-user)과 피어그룹(item or user)이 계산됨
  • 실행 시간 계산
    • 용어
      • $n^\prime << n$: 사용자의 지정된 평점의 최대 수
      • $m^\prime << m$: 아이템의 지정된 평점의 최대 수
      • $n$: 한 쌍의 사용자 간 유사도를 계산하기 위한 최대 실행 시간
      • $m$: 한 쌍의 아이템 간 유사도를 계산하기 위한 최대 실행 시간
    • 사용자 기반 방법론
      • target 사용자의 피어 그룹 계산: $O(m\sdot n^\prime)$ 시간이 요구
      • 모든 사용자의 피어 그룹 계산: $O(m^2\sdot n^\prime)$ 시간이 요구
    • 아이템 기반 방법론
      • $O(n^2\sdot m^\prime)$ 시간이 요구
  • 공간 요구 사항
    • 사용자 기반 방법론: $O(m^2)$
    • 아이템 기반 방법론: $O(n^2)$
    • 사용자 수가 일반적으로 아이템 수보다 많기 때문에, 공간 요구 사항이 대체로 더 큼
• 이웃기반 방법론은 온라인 예측을 할 때 효율적인 경향이 있음
  • 오프라인 단계의 계산 시간에 더 많은 시간을 할당할 수있음

2.3.4 사용자 기반 방법론과 아이템 기반 방법론의 비교

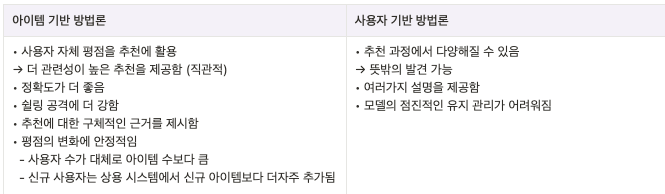
2.3.5 이웃 기반 방법론의 장단점

• 장점
  • 단순함과 직관적인 성격 때문에 적용하기도 쉽고 문제를 파악하기도 쉬움
  • 왜 특정 아이템이 추천됐는지 알기도 쉬움 (아이템 기반 방법론)
• 단점
  • 대규모 환경에서 오프라인 단계가 때로는 비효율적임
    • 사용자 기반 $O(m^2)$ ⇒ m이 커지면 엄청 오래걸림..
    • But 온라인 단계는 항상 효율적임
  • 희박함(sparsity)에 따른 제한된 커버리지
    • 이웃 중 누구도 해당 아이템을 평가하지 않을 경우, 해당 아이템의 예측은 불가능함

2.3.6 사용자 기반과 아이템 기반 방법론의 통합된 관점

두 방법론을 통합하여 평점 행렬 $R$의 엔트리 $r_{uj}$를 예측할 수 있음

• 행과 열간의 코사인 계수를 이용해 target entry (u, j)와 가장 유사한 행, 열을 결정
  • 사용자 기반 방법론(열 이용), 아이템 기반 방법론 (행 이용)
• 위 단계에서 찾은 행과 열의 평점의 가중 조합을 이용해 target entry 예측

2.4 클러스터링과 이웃 기반 방법론

• 이웃 방법론의 주요 문제점: 오프라인 단계에서의 복잡성
  • 사용자 or 아이템 수가 굉장히 클 때 더 나타남
• 클러스터링 기반 방법론의 주요 관점:
  → 오프라인 단계에서의 가장 근접한 이웃 단계를 클러스터링 단계로 대체하는 것
• 특징
  • 각각의 target이 중심이 될 필요 없음
  • 더 작은 피어 그룹을 생성함
  • 클러스터 안에서의 top-k의 가장 근접한 동료가 에측에 활용됨
    → 모든 가능 target에 대해 $O(m^2\sdot n^\prime)$ 시간을 요구하는 것 보다 효율적임
• 클러스터링 세밀도
  • 정확성과 효율성 간의 trade-off 조절
  • 대부분의 경우 효율성의 큰 증가는 정확도의 작은 감소로 이루어짐
• 문제점
  • 평점 행렬이 불완전함 → 클러스터링 방법론은 아주 큰 불완전한 데이터 세트에서 적용됨
• K-means Method
  • 불완전한 데이터에 쉽게 적용될 수 있음
  • k개의 서로 다른 클러스터를 표현하는 k개의 중심 포인트를 이용하는 것
  • m x n 평점 행렬이 불완전하다는 것이 주된 문제점임

★ 2.5 차원 축소와 이웃 기반 방법론

차원 축소 방법론은 이웃 기반 방법론의 품질과 효율성을 높이는데 쓰일 수 있음

차원 축소는 잠재 요인(latent factor)이 있어 저차원이 가능하도록 함

• 차원 축소 방법: SVD, PCA
• SVD 방식의 방법론
  1. 누락된 엔트리를 해당 열의 평균으로 채운다 → 결과 $R_f$
  2. 유사도 행렬 계산 ($S = R^T_fR_f$)
     • 대각화 (Diagonalization): $S = P\Delta P^T$
     • $R_f$의 저차원 표현: $R_fP_d$ ⇒ $R_f$ (m x n) → $P_d$ (n x d) → m x d

2.5.1 바이어스 문제 처리

• 행렬 $R_f$는 불특정 항목을 평균 값으로 작성해 불완전행렬 $R$에서 파생됨
• 이러한 접근 방식은 상당한 bias를 일으킬 가능성이 높음
• 예시

  • 아래 Gladiator 와 Nero는 User Index 1~4까지 똑같음
    → Gladiator는 Nero가 Godfather보다 유사함

  • But Nero의 지정되지 않은 평점을 평균값으로 대체한 후에
    공분산을 보면 Gladiator와 Nero의 공분산이 Godfather보다 크다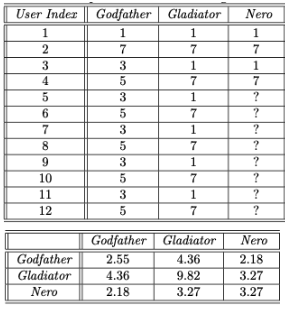

    

2.5.1.1 최대 우도 추정

• 공분산 행렬은 생성 모델의 매개변수를 추정하는 프로세스의 일부로 추정될 수 있다.
• 각 항목 간의 공분산의 최대 우도 추정치는 지정된 항목 간의 공분산으로 추정됨
• 즉, 특정 항목 쌍에 대한 평점을 지정한 사용자만의 정보만 공분산을 추정하는데 사용됨

  • 항목에 공통된 사용자가 없는 경우, 공분산은 0으로 추정

    

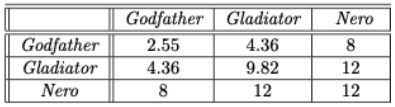
• 행렬에서 지정되지 않은 항목의 비율이 클수록 평균 채우기 기술의 바이어스가 커지게됨
  → 평가된 항목만 활용 (평균으로 채우는 것보다는 우수한 성능을 보임)
• i번째 잠재 백터에 대한 사용자 u의 평균 기여도
  • 이러한 평균 정규화는 다른 사용자가 서로 다른 평점 수를 지정한 경우에 특히 유용함
  • $r_{uj}$: 사용자 u의 항목 j에 대해 관찰된 평점
  • $r_{uj}e_j$: 잠재 백터 $\bar{e_i}$에 대한 프로젝션에 대한 사용자의 기여
  • $I_u$: 사용자 u의 지정된 항목 평점의 인덱스
    

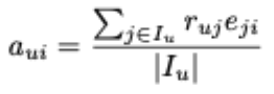
2.5.1.2 불완전한 데이터의 직접 행렬 인수분해

• 평점의 희소성 수준이 높을 때에는 완전히 효과적이지 않음
• 좀더 직접적인 행렬 인수 분해 사용
  
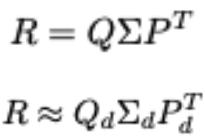
• 장점
  • 축소된 기저 뿐만 아닌 축소된 기저에 해당하는 평점도 알 수 있음
• 문제점
  • 평점 행렬이 완전히 지정되지 않음

★ 2.6 이웃 방법론의 회귀 모델링 관점

• 이웃 사용자의 동일한 항목 / 사용자에 대한 평점의 선형함수로 평점을 예측
• 사용자 기반 이웃 방법의 예측 함수

  • 예측 평점: 동일한 아이템의 다른 평점의 가중 선형 조합

    

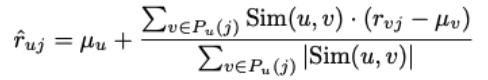
• 선형 회귀에서 평점은 다른 평점의 가중 조합으로 예측되며, 가중치는 최적화 모델을 사용해 결정됨
  • 이웃 기반 접근 방식에서는 선형함수의 계수가 “사용자-사용자 유사도"와 “추론 방식"으로 선택됨
• 조합 가중치로 유사도 값을 사용하는 것은 휴리스틱적이고 임의적임
• 계수는 아이템 간의 상호 종속성을 고려하지 않음
• 모델링 관점에서의 최적성으로 인해, 평점을 결합한 가중치가 더 합리적임

2.7 이웃 기반 방법에 대한 그래프 모델

• 관찰된 평점의 희소성은 이웃 기반 방법의 유사도 계산 문제를 일으킴.
• 유사도를 정의하기 위해 여러 그래프 모델이 사용됨
• 그래프는 네트워크 도메인의 많은 알고리즘 도구를 가능하게 하는 강력한 추상화 작업
• 그래프는 다양한 사용자 or 항목 간의 관계에 대한 구조적 표현을 제공함

2.7.1 사용자-아이템 그래프

• 구조 측정 값을 사용할 수 있음
• 추천 프로세스에 가장자리의 구조적 전이성을 사용할 수 있기 때문에 희소 평점 행렬에 더 효과적
• 노드 간의 간접 연결이라는 개념으로 이웃을 구성할 수 있음
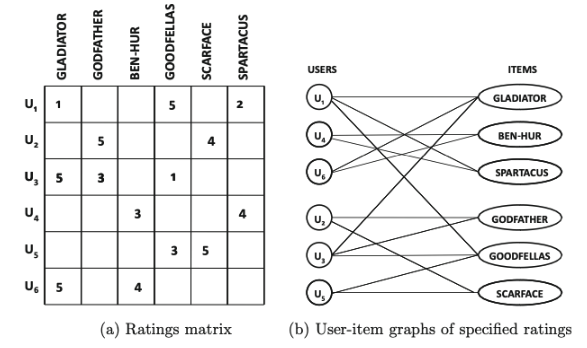
  • 두 사용자가 많은 공통 항목을 평가한 경우 → 가까운 이웃도 고려함
    
• 그래프 표현에서 이웃을 정의하는 방법
  • 랜덤 워크
  • 카츠 척도

2.7.2 사용자-사용자 그래프

• 사용자-아이템 그래프의 짝수 번째 hop으로 정의됨
• 그래프 가장자리가 더 유익하다는 장점이 있음
  • 2-홉 연결이 가장자리를 만드는 동안, 두 사용자간 공통 항목의 수와 유사도를 직접 고려할 수 있기 때문
• 전이성을 사용해 평점을 예측하기 때문에, 매우 희소한 행렬에서 작동할 수 있음
• 정의

  • 호팅

  • 예측 가능성

    

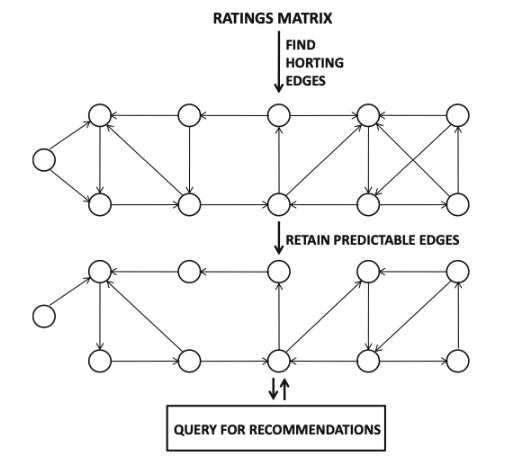
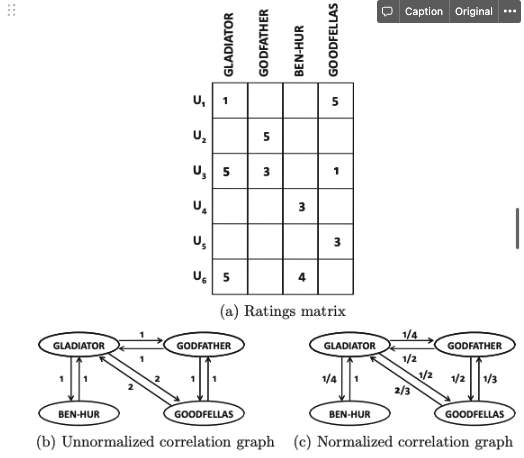
2.7.3 아이템-아이템 그래프

• 상관관계 그래프라고도 불림
• 가장자리의 가중치가 랜덤 워크 확률에 해당하는 그래프가 생성됨
• 상관관계 그래프의 구성에 평점값이 사용되지 않음
• 두 아이템 간에 공통으로 관찰된 평점 수만 사용됨

2.8 Summary

• 협업 필터링은 분류 및 회귀 문제의 일반화로 볼 수 있음
• 사용자 기반 방법은 대상 사용자의 이웃을 확인한다
  • 이웃 계산을 위해 다양한 유사도 함수가 사용됨 (Pearson 상관계수 or 코사인)
  • 이웃은 평점 추정을 위해 사용됨
• 아이템 기반 방법
  • 가장 유사한 아이템은 대상 아이템에 대해 계산됨
  • 유사한 아이템에 대한 사용자 자신의 평점을 사용하여 평점을 예측
  • 관련성이 높은 추천일 수 있지만, 다양한 추천을 얻을 가능성은 적음
• 속도를 높이기 위해 클러스터링이 주로 사용됨
• 데이터 부족으로 인해 수많은 도전에 직면하고 있음
  • 차원 감소 및 그래프 기반 모델(랜덤 워크, 최단 경로 방법론) 활용

Reference

• Recommender Systems: The Textbook, Charu Aggarwal, 2016