- 플로이드-워셜 알고리즘은 '모든 정점'에서 '모든 정점'으로의 최단 경로를 구하고 싶을 때 사용하는 알고리즘이다.
- 플로이드-워셜 알고리즘의 핵심 아이디어는 '거쳐가는 정점'을 기준으로 최단 거리를 구하는 것이다.
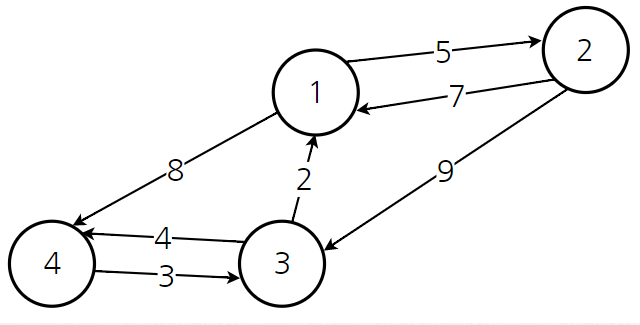
- 위와 같은 그래프가 존재한다고 할 때, 각각의 정점이 다른 정점으로 가는 비용을 이차원 배열의 형태로 나타내면 다음과 같다.
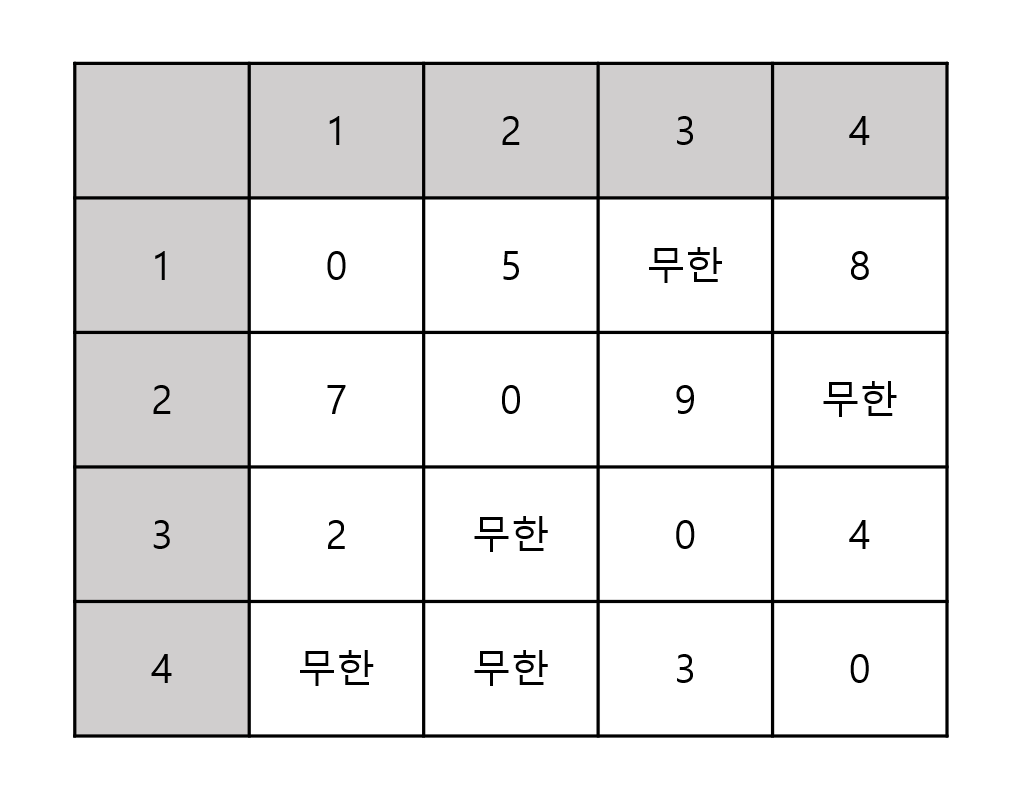
- 위 테이블은 거쳐가는 정점 없이 바로 갈 수 있을 때의 최소 거리를 구한 것으로 '현재까지 계산된 최소 비용'이다.
- 이런 이차원 배열을 반복적으로 갱신하며 최종적으로 모든 최소 비용을 구한다.
- 반복의 기준이 '거쳐가는 정점'이다.
- 노드 1을 거쳐가는 경우
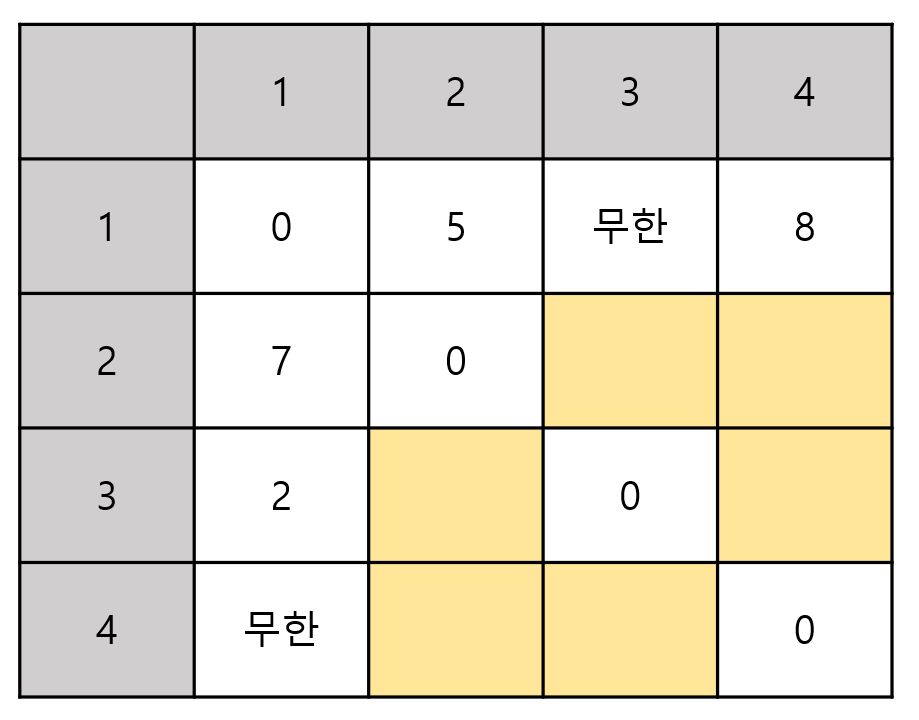
-
노드 1을 거쳐가는 경우는 위의 6개 공간만 갱신해주면 된다.
-
이 때 X에서 Y로 바로 가는 비용과, X에서 노드1을 거친 후 Y로 가는 비용 중 더 적은 비용을 사용한다.
-
X에서 Y로 가는 비용 VS (X에서 노드 1로 가는 비용 + 노드 1에서 Y로 가는 비용)
-
즉, 1을 거쳐서 가는 경우가 더 빠르다면 그 비용으로 갱신해주면 된다는 뜻이다.
-
그럼 다음과 같이 표가 갱신된다.
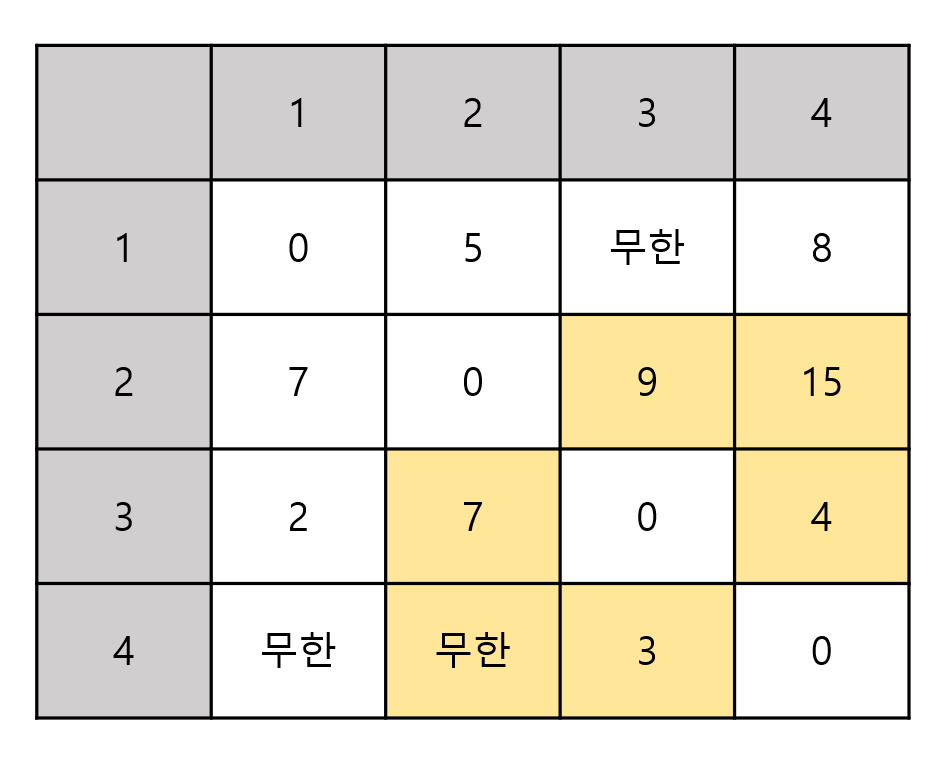
-
이 방식을 모든 노드에 대해서 수행해주면 된다.
- 노드 2를 거쳐가는 경우
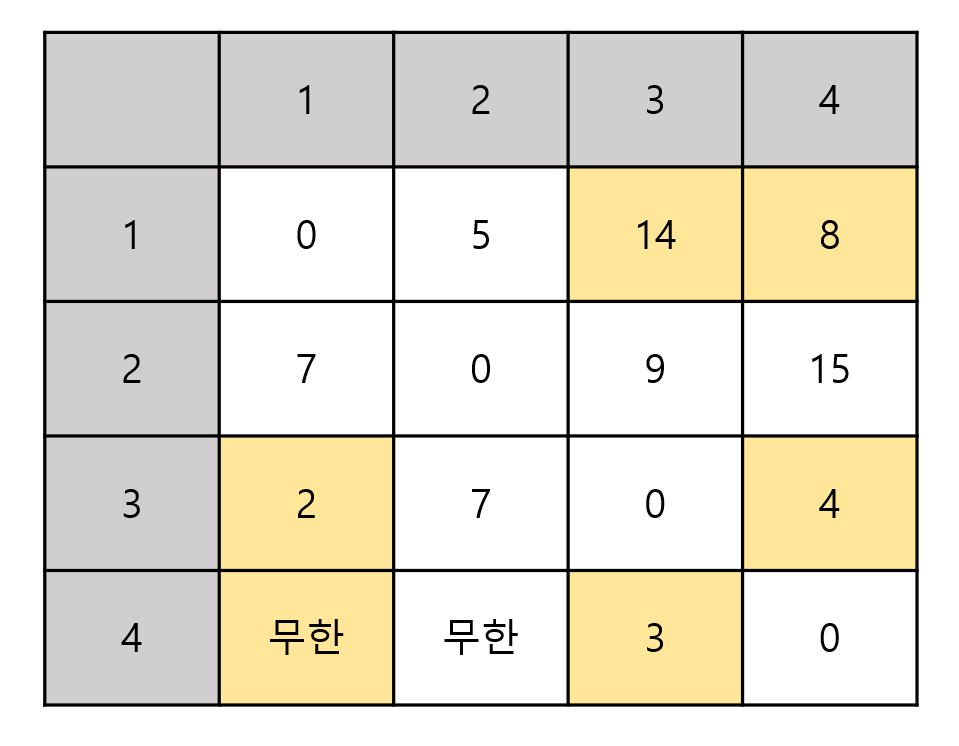
-
최종적으로는 다음과 같은 결과가 나타난다.
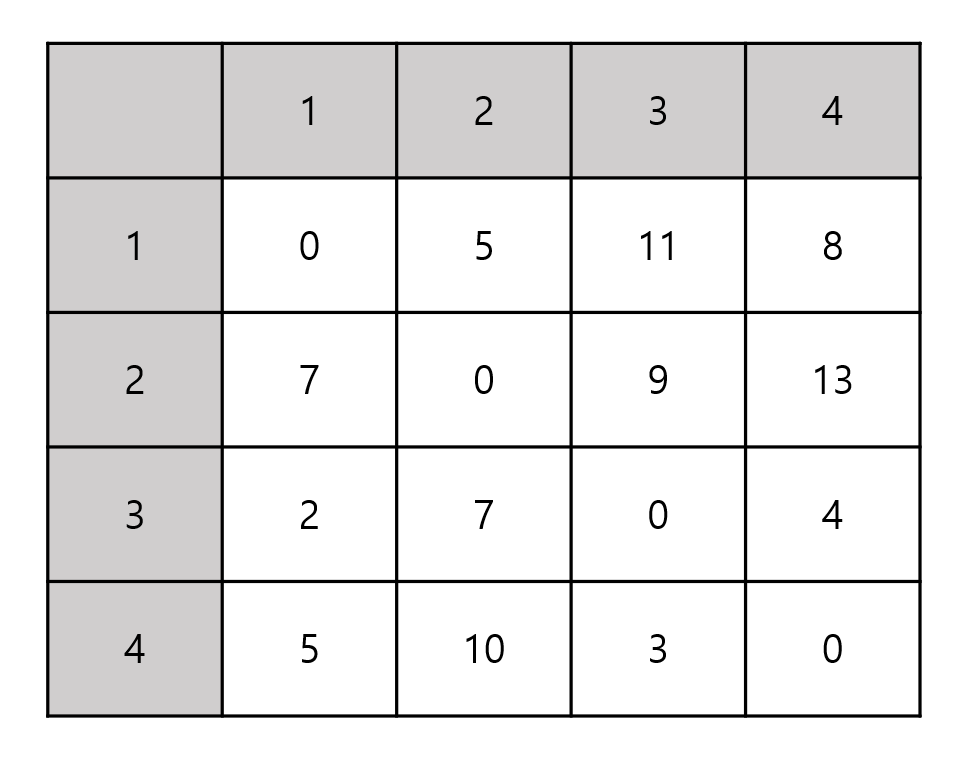
-
해당 결과가 각 노드에서 다른 노드로 이동하는 최단 경로를 나타낸다.
