📌 출처
📝 문제
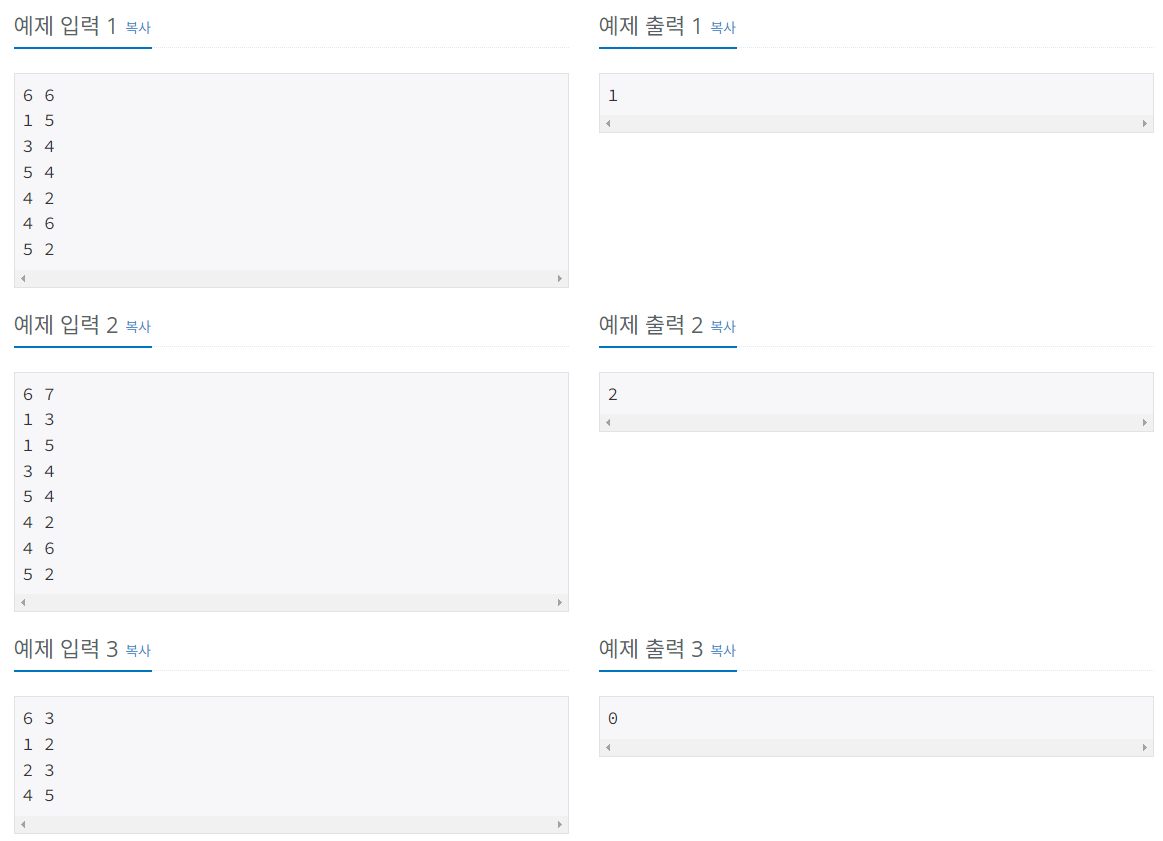
1번부터 N번까지 번호가 붙여져 있는 학생들에 대하여 두 학생끼리 키를 비교한 결과의 일부가 주어져 있다. 단, N명의 학생들의 키는 모두 다르다고 가정한다. 예를 들어, 6명의 학생들에 대하여 6번만 키를 비교하였고, 그 결과가 다음과 같다고 하자.
- 1번 학생의 키 < 5번 학생의 키
- 3번 학생의 키 < 4번 학생의 키
- 5번 학생의 키 < 4번 학생의 키
- 4번 학생의 키 < 2번 학생의 키
- 4번 학생의 키 < 6번 학생의 키
- 5번 학생의 키 < 2번 학생의 키
이 비교 결과로부터 모든 학생 중에서 키가 가장 작은 학생부터 자신이 몇 번째인지 알 수 있는 학생들도 있고 그렇지 못한 학생들도 있다는 사실을 아래처럼 그림을 그려 쉽게 확인할 수 있다. a번 학생의 키가 b번 학생의 키보다 작다면, a에서 b로 화살표를 그려서 표현하였다.
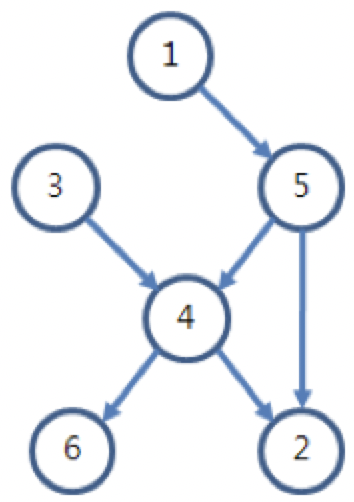
1번은 5번보다 키가 작고, 5번은 4번보다 작기 때문에, 1번은 4번보다 작게 된다. 그러면 1번, 3번, 5번은 모두 4번보다 작게 된다. 또한 4번은 2번과 6번보다 작기 때문에, 4번 학생은 자기보다 작은 학생이 3명이 있고, 자기보다 큰 학생이 2명이 있게 되어 자신의 키가 몇 번째인지 정확히 알 수 있다. 그러나 4번을 제외한 학생들은 자신의 키가 몇 번째인지 알 수 없다.
학생들의 키를 비교한 결과가 주어질 때, 자신의 키가 몇 번째인지 알 수 있는 학생들이 모두 몇 명인지 계산하여 출력하는 프로그램을 작성하시오.
⌨ 입력
첫째 줄에 학생들의 수 N (2 ≤ N ≤ 500)과 두 학생 키를 비교한 횟수 M (0 ≤ M ≤ N(N-1)/2)이 주어진다.
다음 M개의 각 줄에는 두 학생의 키를 비교한 결과를 나타내는 N보다 작거나 같은 서로 다른 양의 정수 a와 b가 주어진다. 이는 번호가 a인 학생이 번호가 b인 학생보다 키가 작은 것을 의미한다.
🖨 출력
자신이 키가 몇 번째인지 알 수 있는 학생이 모두 몇 명인지를 출력한다.
💻 내 코드
1. 리스트를 사용하여 구현
package com.ll.백준.BFS_DFS.p2458;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static int[][] dist;
static int MAX = 1000000;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
dist = new int[N + 1][N + 1];
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= N; j++) {
dist[i][j] = MAX;
if(i == j) {
dist[i][j] = 0;
}
}
}
for(int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
dist[a][b] = 1;
}
for(int k = 1; k <= N; k++) {
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= N; j++) {
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
int result = 0;
for(int i = 1; i <= N; i++) {
int cnt = 0;
for(int j = 1; j <= N; j++) {
if(dist[i][j] != MAX || dist[j][i] != MAX) cnt++;
}
if(cnt == N) result++;
}
System.out.println(result);
}
}✏ 설명
1번 학생부터 2~N번까지 모든 학생과 비교 가능한지 파악하고, 2번 학생부터 1, 3~N번까지 모든 학생과 비교 가능한지 파악해야 한다.
이렇게 N번의 학생까지 매번 연산을 할 경우 시간초과가 발생하게 된다.
그래서, 모든 학생들이 서로 키를 비교할 수 있는지, 모든 경로를 한번에 구해놓고, 1~N번의 학생들을 보면서 비교 가능한지만 체크해야 한다.
이럴 때 사용하는 것이 플로이드 워셜 알고리즘이다.
for(int k = 1; k <= N; k++) { // 경유지
for(int i = 1; i <= N; i++) { // 출발지
for(int j = 1; j <= N; j++) { // 도착지
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}3중 for문을 통해 (출발지-도착지)의 경로와 (출발지-경유지-도착지)의 경로를 비교하며 최단경로 값을 비교한다.
이렇게 돌고 나면 출발지와 도착지가 어떤 식으로도 연결이 안되어 있는 경우에는 MAX 값으로 남아있을 것이다.
그 말은 즉, 두 학생의 키는 비교할 수 없다는 뜻이 된다.
따라서 위와 같이 최단 경로를 구해놓고 다시 2중 for문을 돌면서 모든 노드와 연결이 되어 있는 학생을 찾으면 된다.
- 시간복잡도
- 플로이드 워셜은 N^3의 시간복잡도를 갖는다.
- N은 500이므로 500^3 = 125,000,000으로 엄격한 시간복잡도를 갖는 문제에서는 시간초과가 발생할 수 있지만 해당 문제에서는 큰 무리가 없었다.
- 일반적으로 N이 500 이하인 경우에만 플로이드 워셜이 가능하다. (일부 기업 알고리즘 테스트에서는 300이하)
