[백준]14500번 : 테트로미노

📌 출처

14500번 : 테트로미노

📝 문제

폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.

정사각형은 서로 겹치면 안 된다.
도형은 모두 연결되어 있어야 한다.
정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.

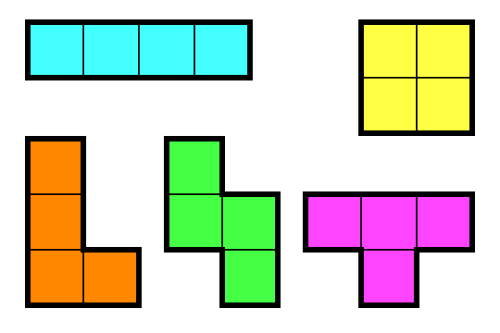
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.

테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.

테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.

⌨ 입력

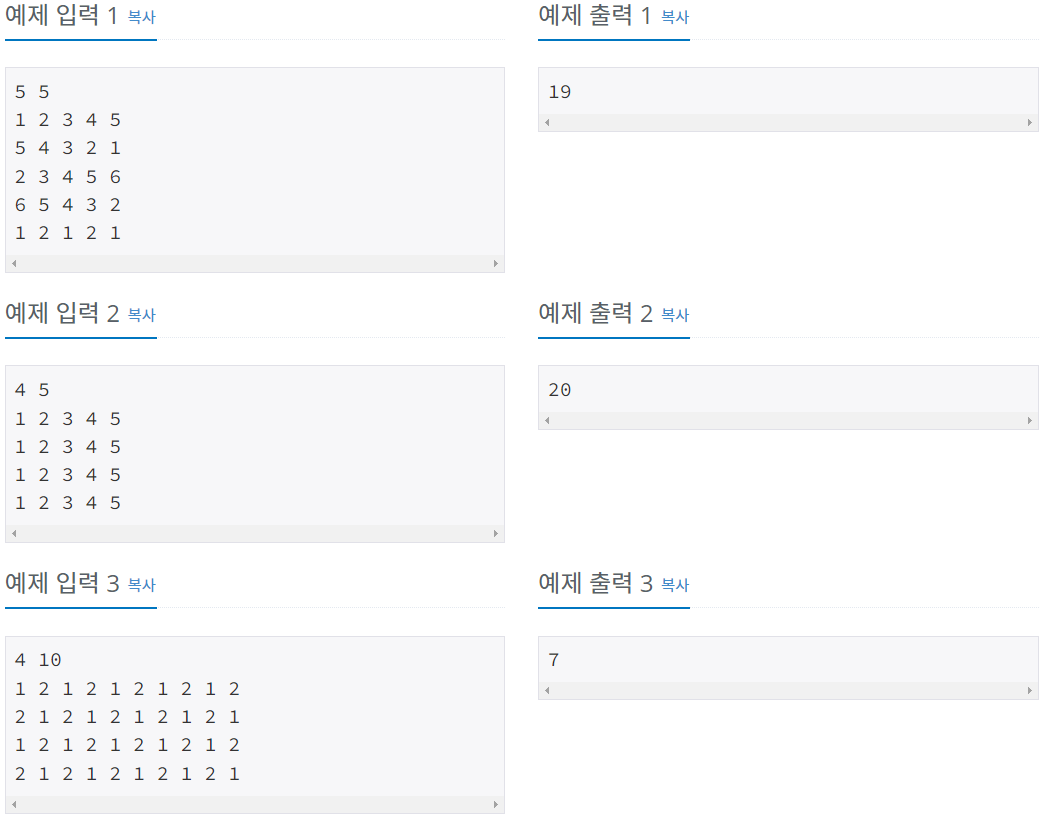
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)

둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.

🖨 출력

첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.

💻 내 코드

1. 리스트를 사용하여 구현

package com.ll.백준.완전탐색;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class p14500 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());
        int[][] map = new int[N][M];

        int[][][] tetromino = new int[][][]{
                {{1, 1}, {1, 1}},
                {{1, 0}, {1, 1}, {1, 0}},
                {{0, 1, 0}, {1, 1, 1}},
                {{0, 1}, {1, 1}, {0, 1}},
                {{1, 1, 1}, {0, 1, 0}},
                {{1, 0}, {1, 0}, {1, 1}},
                {{0, 0, 1}, {1, 1, 1}},
                {{1, 1}, {0, 1}, {0, 1}},
                {{1, 1, 1}, {1, 0, 0}},
                {{0, 1}, {0, 1}, {1, 1}},
                {{1, 0, 0}, {1, 1, 1}},
                {{1, 1}, {1, 0}, {1, 0}},
                {{1, 1, 1}, {0, 0, 1}},
                {{0, 1, 1}, {1, 1, 0}},
                {{1, 0}, {1, 1}, {0, 1}},
                {{1, 1,0}, {0, 1, 1}},
                {{0, 1}, {1, 1}, {1, 0}},
                {{1, 1, 1, 1}},
                {{1}, {1}, {1}, {1}}
        };

        for(int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            for(int j = 0; j < M; j++) {
                map[i][j] = Integer.parseInt(st.nextToken());
            }
        }


        int max = 0;

        for(int i = 0; i < tetromino.length; i++) {
            int maxTmp = 0;
            for(int j = 0; j <= N - tetromino[i].length; j++) {
                for(int k = 0; k <= M - tetromino[i][0].length; k++) {
                    int result = 0;
                    for(int l = 0; l < tetromino[i].length; l++) {
                        for(int m = 0; m < tetromino[i][0].length; m++) {
                            if(tetromino[i][l][m] == 1) {
                                result += map[j + l][k + m];
                            }
                        }
                    }
                    maxTmp = Math.max(maxTmp, result);
                }
            }
            max = Math.max(max, maxTmp);
        }

        System.out.println(max);
    }
}

✏ 설명

무식하게 해버렸다.
나올 수 있는 모든 테트로미노의 경우를 생각해봤더니 총 19가지의 경우가 나왔다.
map의 크기는 최대 500X500 이므로 총 계산 횟수는 500X500X19X4 = 1900만.
시간 안에 계산이 가능하기 때문에 별다른 고민 없이 냅다 모든 테트로미노의 경우를 만들어버렸다.
5개 만들어놓고 회전 이런 것도 없이 그냥 19개를 싹 다 만들어버렸다..ㅎ
분명 더 효율적인 코드가 있을 것 같기는 하지만 시간 싸움인 코딩 테스트에서 이정도면 충분히 좋은 코드라고 생각한다.(지극히 개인적)