[백준] 1967번 : 트리의 지름

📌 출처

1967번 : 트리의 지름

📝 문제

트리(tree)는 사이클이 없는 무방향 그래프이다. 트리에서는 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재하게 된다. 트리에서 어떤 두 노드를 선택해서 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우가 있을 것이다. 이럴 때 트리의 모든 노드들은 이 두 노드를 지름의 끝 점으로 하는 원 안에 들어가게 된다.

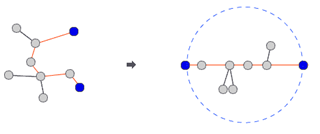
이런 두 노드 사이의 경로의 길이를 트리의 지름이라고 한다. 정확히 정의하자면 트리에 존재하는 모든 경로들 중에서 가장 긴 것의 길이를 말한다.

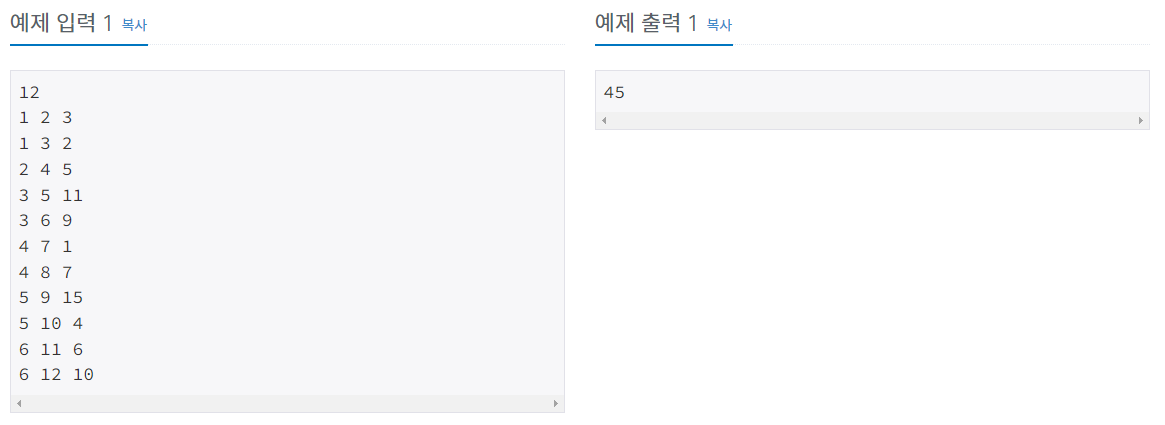
입력으로 루트가 있는 트리를 가중치가 있는 간선들로 줄 때, 트리의 지름을 구해서 출력하는 프로그램을 작성하시오. 아래와 같은 트리가 주어진다면 트리의 지름은 45가 된다.

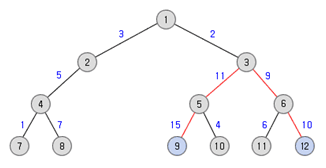
트리의 노드는 1부터 n까지 번호가 매겨져 있다.

⌨ 입력

파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연결하는 두 노드 중 부모 노드의 번호를 나타내고, 두 번째 정수는 자식 노드를, 세 번째 정수는 간선의 가중치를 나타낸다. 간선에 대한 정보는 부모 노드의 번호가 작은 것이 먼저 입력되고, 부모 노드의 번호가 같으면 자식 노드의 번호가 작은 것이 먼저 입력된다. 루트 노드의 번호는 항상 1이라고 가정하며, 간선의 가중치는 100보다 크지 않은 양의 정수이다.

🖨 출력

첫째 줄에 트리의 지름을 출력한다.

💻 내 코드

1. 리스트를 사용하여 구현

package com.ll.백준.BFS_DFS.p1967;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class Main {
    static int n, distance, bigNode;
    static ArrayList<Node>[] nodes;
    static boolean[] visited;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        n = Integer.parseInt(br.readLine());
        nodes = new ArrayList[n + 1];
        visited = new boolean[n + 1];

        for(int i = 0; i < n + 1; i++) {
            nodes[i] = new ArrayList<>();
        }

        for(int i = 0; i < n - 1; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());

            nodes[a].add(new Node(b, w));
            nodes[b].add(new Node(a, w));
        }

        bigNode = 1;
        distance = 0;
        visited[1] = true;
        dfs(bigNode, 0);

        visited = new boolean[n + 1];
        visited[bigNode] = true;
        distance = 0;
        dfs(bigNode, distance);

        System.out.println(distance);
    }

    static class Node {
        int num;
        int weight;

        Node(int num, int weight) {
            this.num = num;
            this.weight = weight;
        }
    }

    static void dfs(int nodeNum, int distanceSum) {
        if(distance < distanceSum) {
            distance = Math.max(distance, distanceSum);
            bigNode = nodeNum;
        }

        for(Node node : nodes[nodeNum]) {
            if(!visited[node.num]) {
                visited[node.num] = true;
                dfs(node.num, distanceSum + node.weight);
            }
        }
    }
}

✏ 설명

이번 문제는 어렵다기보다는 어색했던? 문제였다.
여태까지 내가 풀어왔던 그래프 탐색 문제들은 NXM으로 주어졌는데 이건 그런 형태가 아니라 트리의 형태로 주어졌다.
그래서 조금 풀이가 어색했던 것 같다.

문제의 해결 방안은 다음과 같다.

• 루트 노드에서 가장 먼(가중치가 큰) 노드를 찾는다. (DFS)
• 그 노드에서 가장 먼 노드를 찾는다. (DFS)

즉, DFS을 2번 사용하면 해결되는 문제이다.

특이점?이랄까 내가 기억해야 하는 부분을 정리해보자.
우선 트리 형태로 데이터가 주어질 경우 양방향으로 움직일 수 있다.
그래서 1 2 3 이런 식으로 데이터가 주어졌을 때
1에서 2로도 이동할 수 있고 2에서 1로도 이동할 수 있다.
그래서 2개로 나눠서 저장을 한다.
1->2 가중치 3, 2->1 가중치 3 이런식으로

그렇게 각 노드 별로 어떤 노드로 연결되어있는지 다 정리를 한 다음 DFS를 진행한다.
DFS는 그냥 내가 아는 방식으로 진행해나가면 된다.