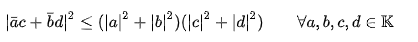
참고 : KoreaUniv DSBA 영상
1. Bias-Variance Decomposition 수학적 정의
답을 알 수 없는 예측 데이터(Target)에 대한 오차의 기대값을 모델의 Bias와 Variance로 분해하는 것
1) 모델에는 "추가적인 에러(=노이즈)"가 발생한다.
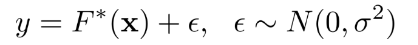
- F*(x) = 알지못하는 Target function
- e = 독립적이고 동일한 분포인 에러
2) 가능한 데이터셋들을 모두 Expectation 한 것 (=평균)
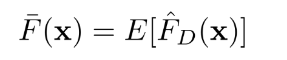
3) MSE를 이용해 편향 분산 구하기

- Bias^2 : 평균적인 추정값이 진짜 정답과 얼마나 차이가 나는가
- Variance : 개별 추정값들이이 평균대비로 얼마나 퍼져있는가
- ^2 : Irreducible error 사람이 컨트롤할 수 없는 자연 발생적인 변동성
- Bias와 variance는 독립적이 아님 (Bias Variance Trade-off)
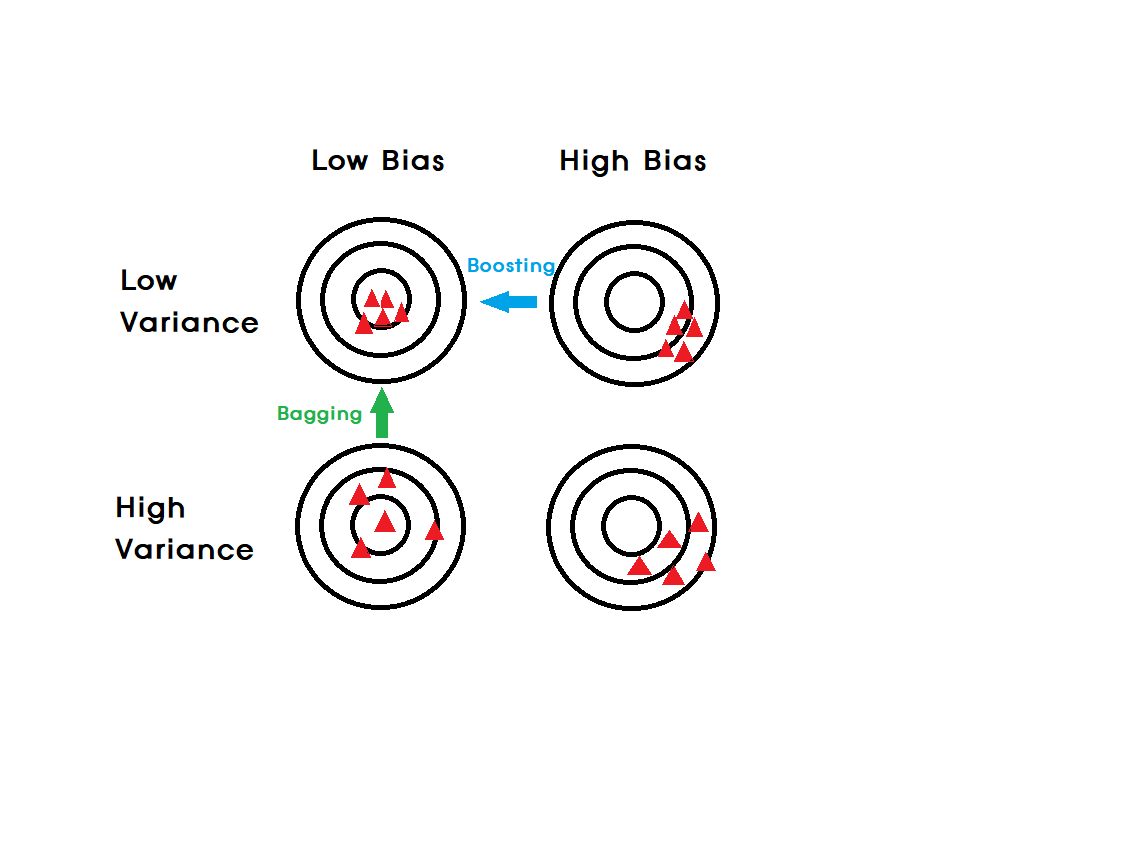
2. Bias-Variance decomposition 직관화
위의 식을 그림으로 나타냄.
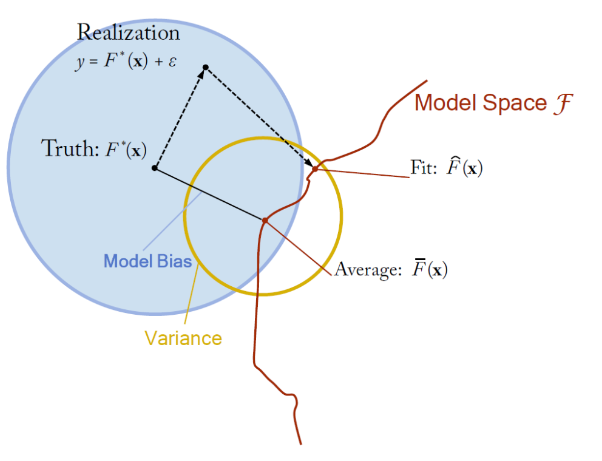
-
Bias(편향) :
Low bias : 반복적으로 수행했을 때 평균적으로 잘 맞출 수 있음
High bias : 과소 적합(under-fitting). 지나치게 단순한 모델로 인한 error. 모델이 무언가 중요한 것을 놓치고 있음(=A poor match) -
Variance(분산) :
Low variance : 노이즈가 바뀌어도(=다른 데이터셋) 함수 추정값이 큰 영향을 받지 않음
High variance : 과대 적합(Over-fitting). 지나치게 복잡한 모델로 인한 error. 일반화가 되지 않은 모델 (=A weak match)
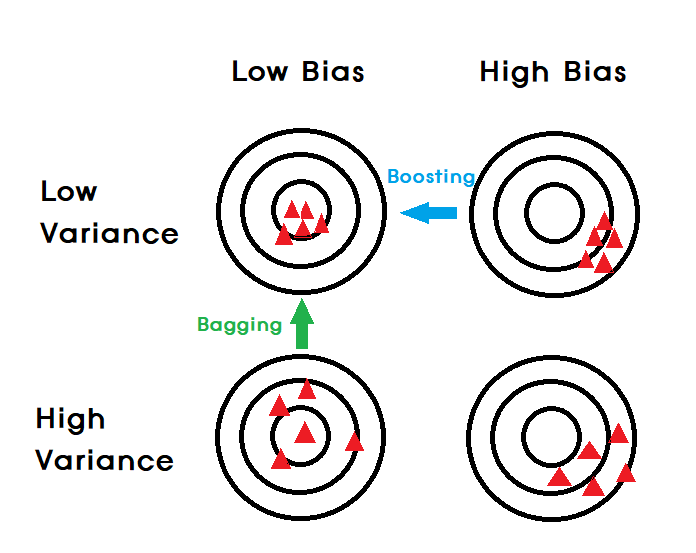
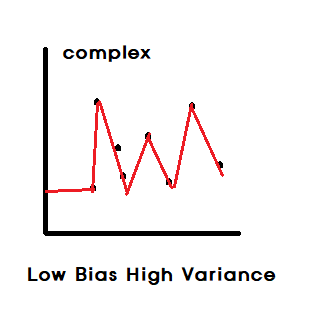
- Higher model complexity : Low Bias & High Variance
ex)
Decision Tree(의사결정나무) : 가지치기를 하지 않은 경우
ANN(인공신경망),SVM : 커널을 좁게 만든 경우
K-NN : K값을 작은 경우
=> 복잡도가 높은 모델들은 Bagging과 합이 잘 맞음
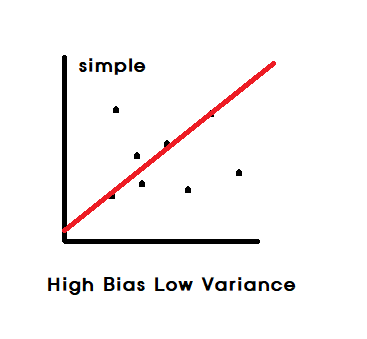
- Lower model complexity : High Bias & Low Variance
ex)
Logistic Regression(회귀와 같은 정규화기법)
LDA
K-NN : K값이 큰 경우
=> 복잡도가 낮은 모델들은 Boosting과 합이 잘 맞음
3. 앙상블의 목적
1. 앙상블의 목표 : 개별 모델을 합침으로써 오류를 줄임
- 분산을 줄이기 위해 : Bagging, Random Forests 사용
- 편향을 줄이기 위해 : Boositing 사용
2. 핵심
-
개별 모델들이 어떻게 하면 충분한 수준의 다양성(sufficient degree of diversity)을 얻을 수 있을까?(=서로 어떻게 하면 다른 모형을 만들어 낼 수 있을까?)⭐⭐⭐⭐⭐
-
개별 모델들을 어떻게 잘 결합할 것인가?
3. sufficient degree of diversity
= 동일한 모델들을 합치는 것은 아무 의미 없다.
- 적절히 다른 모델들을 합친 앙상블 모델
- 일정 수준 이상의 다양성을 확보함을 동시에 개별 모델 또한 적절한 성능이 있어야한다.
(certain element of diversity + retaining good performance individually)

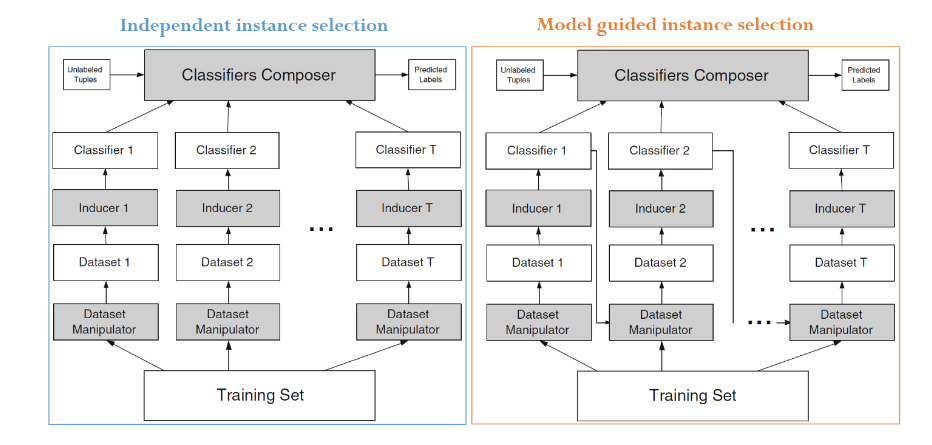
- 왼쪽은 Bagging 오른쪽은 Boosting 기법이다.
- Bagging은 병렬처리가 가능(개별학습의 계산복잡도가 높기때문에 오래걸림. 병렬처리라고 항상 빠른건 아님.)
- Boosting은 순차처리만 가능
4. 앙상블의 효과 수식으로 이해하기


- M : 실제 앙상블의 구성 요소
- E(Avg) : x가 주어졌을 때 m번째 모델에 의해 만들어지는 에러 제곱의 평균
- E(Ensemble) output : 앙상블의 기본 출력을 개별 모형 출력의 평균으로 정의함. 가장 기본적인 앙상블 방법론이며 가장 효과가 떨어짐.

- 비현실적 : 이론적으로 개별 모델이 독립이라는 가정 하에 앙상블의 에러값은 개별모형의 에러값의 M분의 1만큼 줄어든다. 현실적으로는 불가능.
- 앙상블 에러의 제곱 안의 M분의 1을 바깥으로 빼면 M^2분의 1이 되기 때문에 위의 식이 된다.
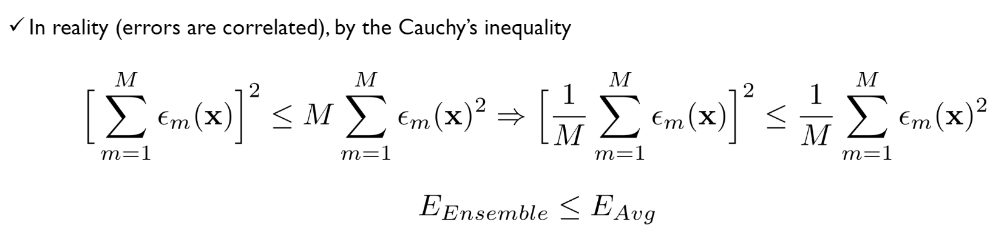
-
현실적(코시-슈바르츠 부등식을 이용) : 현실적으로 개별 모델이 독립이 아니라는 가정 하에서도 평균보다는 앙상블의 에러가 작다.(성능이 좋다) 실제로도 제일 성능이 좋은 개별모델보다 앙상블의 성능이 좋음.