Material Point Method for Snow Simulation (SIGGRAPH 2013)

mpm........
1. Introduction
3. Paper Overview
4. Material Point Method
4-1. Full Method
1. Rasterize particle data to the grid
- transfer mass and velocity to the grid
- mass
min=∑pmpwipn
- velocity (운동량 보존을 위한 식)
vin=∑pvpnmpwipn/min
2. Compute Particle volumes and densities
- 첫 time step 에서만 실행
- particle의 부피 설정
- Cell의 밀도
mi0/h3
- particle의 가중치와 Volume
ρp0=∑imi0wip0/h3
Vp0=mp/ρp0
3. Compute grid forces
4. Update velocities on grid
- Section 10 using vi∗
5. Grid-based body collisions
- Section 8 (Body Collision) using vi∗
6. Solve the linear system
- implicit) Eq.9 for semi-implicit integration
- explicit) vin+1=vi∗ 로 계산
7. Update deformation gradient
- Fpn+1=(I+Δt∇vpn+1)Fpn
- ∇vpn+1=∑ivin+1(∇wipn)T
- Section 7
8. Update particle velocities
- new particle velocities
vpn+1=(1−α)vPICpn+1+αvFLIPpn+1
- PIC part
vPICpn+1=∑ivin+1wipn
- FLIP part
vFLIPpn+1=vpn+∑i(vin+1−vin)wipn
- α
α=0.95
9. Particle-based body collisions
- Section 8 using vpn+1
10. Update particle positions
- xpn+1=xpn+Δtvpn+1
5. Comstitutive Model
- hyperelasticity 에 있어서 finite-strain multiplicative plasticity 를 간소화함
- plastic yield criteria : using principal stretches
- hyperelasticity energy density : using Lame parameters
- Elasto-plastic energy density function
Ψ(FE,FP)=μ(FP)∣∣FE−RE∣∣F2+2λ(FP(JE−1)2 - Eq(1)
F: Deformation Gradient (F=FEFP)
FE : elastic part , FP : plastic part
- plastic deformation gradient
μ(FP)=μ0eξ(1−JP) and λ(FP)=λ0eξ(1−JP) - Eq(2)
JE=def(FE) and JP=det(FP), FE=RESE
λ0,μ0 : initial Lame coefficient
ξ : dimensionless plastic hardening parameter
θc and θs : compression and stretch thresholds to start plastic deformation(fracture)
-> FE의 값을 [1−θc, 1+θs]로 제한
- deforming plastically
- small deformation 영역에서는 elastic (FE dependency)
- deformation gradient 가 threshold를 넘은 경우, deforming plastically (Section.7)
- Eq.2에 나온 material property 를 변화시킴
- 압력(packing)에 있어서는 크게
- stretch(farcture)에 있어서는 작게
- Threshold
- θc and θs : material이 breaking 되는 시간 결정
- Parameters
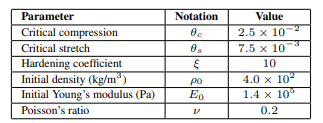
6. Stress-based forces and linearization
- Total elastic potential energy -> energy density Ψ
∫Ω0Ψ(FE(X), FP(X))dX -Eq (3)
- stress-based forces에 대한 MPM 공간 이산화 = Eulerian grid node material positions에 대한 에너지의 이산 근사값을 미분한 것
-> BUT Eulerian 그리드는 변형되지 않으므로, 그리드 노드의 위치 변화는 그리드 노드의 속도에 의해 결정된다.
- 수식
- 변경된 그리드 노드의 위치
xi : 그리드 노드 i의 위치
x^i=xi+Δtvi : 현재 그리드 속도 vi에 대한 그리드 노드의 deformation location
- total elastic potential
Φ(x^)=∑pVp0Ψ(F^Ep(x^),FPpn) : total elastic potential
(vector of all nodes x^i denote to x^)
VP0 : 처음에 particle p가 차지한 volume
FPpn : time tn에서의 particle p의 plastic part of F
- F^Ep
F^Ep : x^의 elastic part
-> F^Ep(x^)=(I+∑i(xi^−xi)(∇wipn)T)FEpn - Eq(4)
- stress-based forces에 대한 MPM 공간 이산화
−fi(x^)=∂xi^∂Φ=∑pVp0∂FE∂Ψ(F^EP(x^),FPPn)(FEPn)T∇wipn - Eq(5)
fi(x^) : 그리드 노드 i에서 elastic stress에 대한 힘
-> Cauchy stress로 표현
σp=Jpn1∂FE∂Ψ(F^EP,FPPn)(FEPn)T 사용해서
fi(x^)=−∑pVpnσp∇wipn - Eq(6)
Vpn=JpnVp0 : 시간 tn 에 particle p에 의해 차지된 물질의 부피
- Grid velocity update가 목표
- 앞에서 말한 것들은 MPM 공간 이산화와 elastic potential 간의 관계
- Full method 3에서 말한 compute grid forces 단계에 사용
- potential에 대한 Hessian 사용해서 elastic part의 implicit step update표현
−δfi=∑j∂xi^∂xj^∂2Φ(x^)δuj=∑pVp0Ap(FEPn)T∇wipn -Eq (7)
AP=∂FE∂FE∂2Ψ(FE(x^),FPPn):(∑jδuj(∇wjpn)TFEPn) -Eq (8)
-> A=C:D 뜻은 Aij=CijklDkl
6.1 Semi-implicit update
- temporary defining
F^PPn+1=(I+Δt∇vpn+1)FEPn and F^PPn+1=FPPn
-> 초기의 변화는 deformation gradient 의 elastic part에 영향을 미친다.
FPn+1=(I+Δt∇vpn+1)FEPnFPPn=F^EPn+1F^PPn+1
- Next Step
- F^EPn+1중에서 critical deformation threshold를 넘는 것을 F^PPn+1에 넣기
- SVD 써서 F^EPn+1=UPΣ^pVpT
Σp=clamp(Σp^,[1−θc,1+θs])
- Final
- elastic and plastic component of deformation gradient
FEPn+1=UpΣpVpT and FPPn+1=VpΣp−1UpTFpn+1
따라서 Fpn+1=FEpn+1FPpn+1
8. Body Collisions
- collision check twice in each time step
- 1st : grid velocity에 힘이 가해진 직후의 grid velocity vi∗
- 2nd : particle velocity vpn+1의 위치를 업데이트 하기 전 보간에 의한 소실을 막기 위해서
- in case of collision
n=∇ϕ : local normal
vco : object velocity
- v : particle/grid velocity
-> transform into reference frame of the collision object
-> vrel=v−vco
if) bodied separate (vn=vrel⋅n≥0) -> no coliision
let) vt=vrel−nvn : tangential portion of the relative velocity
-> if) sticking impluse required (∣∣vt∣∣≤−μvn) -> vrel′=0
-> if) dynamic friction vrel′=vt+μvnvt/∣∣vt∣∣ (μ : coefficient of friction)
- Finally
v′=vrel′+vco
-> relative velocity back into world coordinates
- Types of Collision objects
- Rigid Case
- Deforming Case
- Finally
- sticky collision
- vrel′=0



