Computer Animation Ch.12

Special Models for Animation

12.1 Implicit Surfaces

• 음함수로 정의된 primitive 함수의 합을 이용해서 음함수로 구성하여 애니메이션에 유용한 객체를 정의하는 음함수 곡면을 만든다.
• 음함수 곡면은 부드럽고 유기적인 형태를 구성하는데 적합하다.
  • 액체, 구름, 동물모양 등을 모델링 하는데 유용하다.

12.1.1 Basic Implicit Surface Formulation

• 음함수 곡면은 $f(P)=0$ 을 만족하는 점들의 집합으로 정의되고, 양함수로 표현되지 않고 음함수로만 정의된다.
• 음함수 곡면은 광선 추적법을 이용하여 곡면의 점을 찾아낸다.
  • 음함수 곡면을 양함수 형태의 다각형으로 만들 수 있다.
  • 메쉬의 정점에 있는 음함수 값들은 음함수 곡면에 놓여있는 점들은 보간을 통해 값을 얻는다.
• 가장 잘 알려진 음함수 primitive는 metaball이다.
  
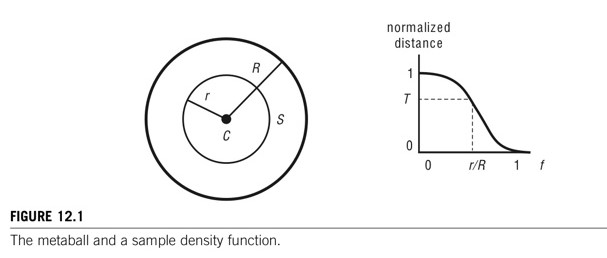
  • 중심점($C$), 작용 반지름($R$), 밀도 함수($f$), 임계 값($T$)
  • $f(distance(P,C)/R-T)=0$ 을 만족시키는 점 집합이 곡면 $S$를 정의한다.
  • $r$은 분리된 metaball을 표현하기 위해 정의된 곡면에 있는 거리이다.(함수 $f$를 측정하는 경계값)
  • $F(P)=\sum w_if_i(P)-T$ 식을 통해 일반화 시킬 수 있다.
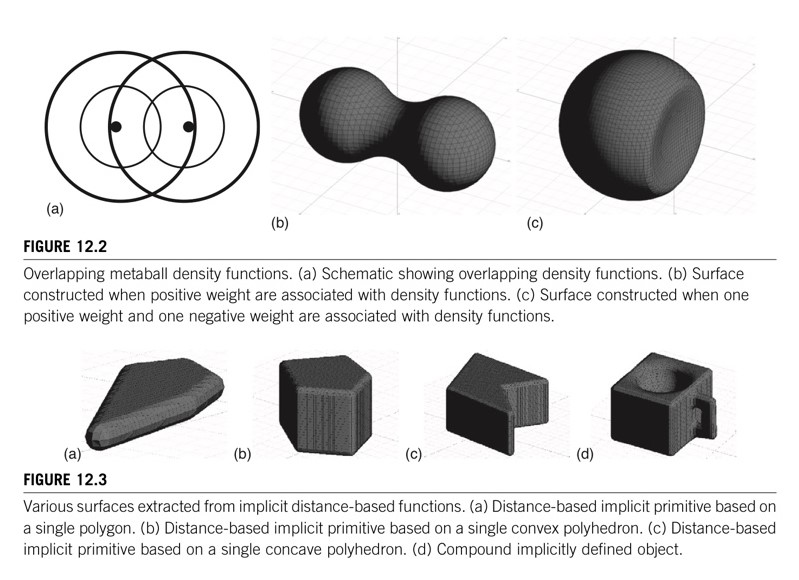
    • 가중치($w_i$) 일반화를 통해 음함수가 부드러운 곡면이 되도록 할 수 있다. 가중치는 원하는 곡면을 구성하기 위해 사용자에 의해 임의로 결정된다.(Figure 12.2)
    • 함수($f_i$) 일반화를 통해 색다른 객체를 만들 수 있게 해준다.(더 복잡한 객체) (Figure 12.3)

12.1.2 Animation Using Implicity Defined Objects

• 음함수 곡면의 형태를 수정함으로써 애니메이션 효과를 얻을 수 있다.
  • 중심원소의 움직임 제어
  • 구름, 물 모델링
• 음함수 곡면의 매개 변수를 수정함으로써 생성할 수 있다.
  • 뭉그러짐과 팽창의 효과
  • 방향성과 속도, 가속도에 영향

12.1.3 Collision Detection

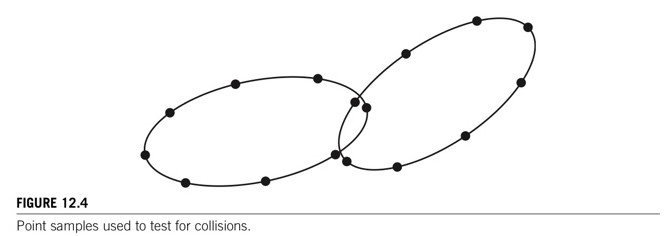
• 음함수 형태로 표현된 객체는 충돌 검출에 적합하다.
• 한 객체의 곡면에 있는 표본 점들은 충돌을 검사하려는 공간의 음함수 값을 구함으로서 충돌하는지 확인할 수 있다. (Figure 12.4)
  • 객체의 표본점들의 밀도에 정확성이 의존된다.
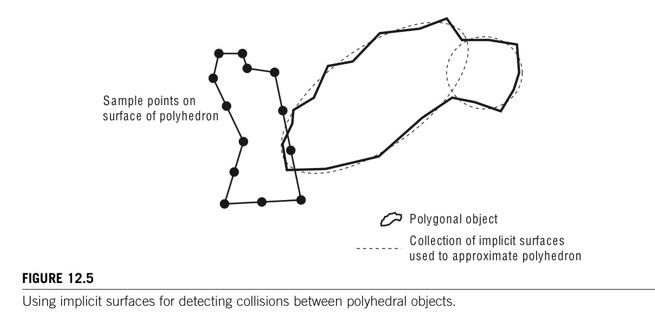
• 음함수와 다면체의 충돌에도 이용할 수 있다. (Figure 12.5)
  • 다면체 곡면에 근사적인 음함수의 정확도에 의존된다.

12.1.4 Deforming the Implicit Surface as a Result of Collision

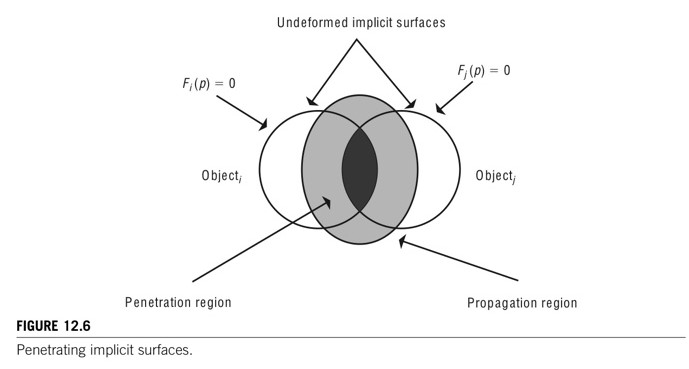
• 두개의 음함수 곡면 객체와의 충돌을 먼저 찾는다.
  • 겹쳐지는 지역을 침투영역(penetration region), 침투 영역에 인접한 외면의 영역을 확대영역(propagation region) 이라고 한다. (Figure 12.6)
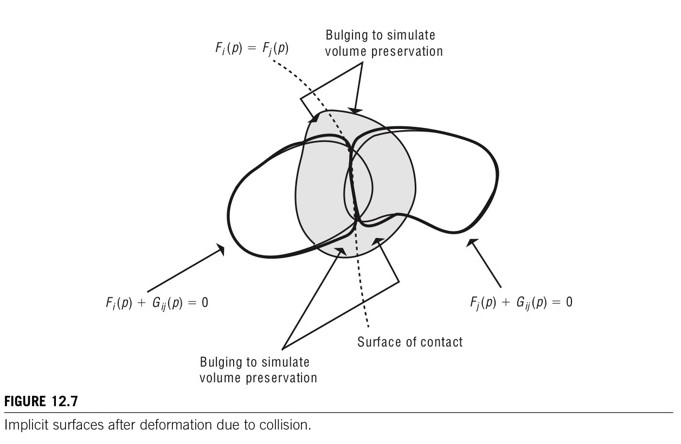
• 각 객체의 밀도 함수는 다른 객체의 중첩 밀도 함수에 의해 수정된다.
  • 음함수는 중첩 영역에서 일치하여 접촉면을 만든다. (Figure 12.7)
  • 침투 영역에서 $G$는 충돌의 결과로 인해 음의 부호를 가진다.
    • $G_{ij}=-F_j(p)$ , $G_{ji}=-F_i(p)$
  • 부피 보존을 시뮬레이션 하기 위해서 $G$ 함수에 추가 항을 더한다.
    • 침투 영역에 바로 인접한 확대 영역에서 양의 값을 가지도록 한다.
    • 음함수 곡면을 팽창시킨다.
  • 확대 영역에서 $G(p)$는 상호 침투 영역의 경계 간 거리인 $h$로 정의된다.
    • 확대 영역과 상호 침투 영역 사이의 연속성을 보장하기 위해 $h'(0)$ 은 $p$점에서 $G$의 방향 도함수와 같아야 한다.

12.1.5 Level Set Methods

• 단계 집합 방법(Level Set Methods)은 음함수 곡면에 활동성을 추가한다.
• 객체에 대한 격자 표현을 이용하여 부호화된 거리 함수로 실행한다.
• 값이 수정되면, 부호화된 거리 함수에 오류가 생기므로 재정규화를 실행한다.

12.2 Plants

• 식물은 제한적인 분기 구조를 가지며, 하나의 원본으로 부터 자라 개별요소가 성장함에 따라 분기 구조를 발달시킨다.
• 파티클과 프렉탈, L-System을 사용하여 모델링 된다.
• 식물학의 위상은 재귀적인 분기 구조를 이용하여 특징을 나타낼 수 있다.
  • 이차원 분기 구조
• 분기 구조의 부호화는 식물 모델링의 목표이다.

12.2.1 A Little Bit of Botany

12.2.2 L-Systems

• L-System은 병렬 재작성 시스템(parallel rewriting system)이다.
• L-System의 가장 단순한 부류는 deterministic이고 문맥자유(context-free) L-System이다.
  • D0L-System이라고도 한다.
  • 선행자와 후행자의 형태를 가지는 생성 규칙의 집합이다.
• L-System의 기하학적 보간
  • L-System으로 생성된 문자열을 이미지로 만들기 위해 기하학적인 해석이 필요하다.
  • 기하학적 대체
    • 각 문자에 대응되는 기하학적 요소를 사용하여 대체시킨다.
  • 터틀 그래픽스
    • 각 기호에 따라 정해진 행동을 수행하여 문자열을 기하적 요소로 대체시킨다.
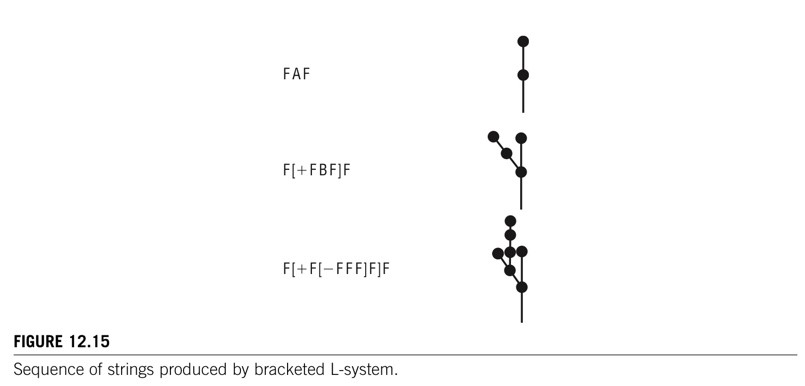
• 꺽쇠형 L-System (Figure 12.15)
  • 단일 세그먼트 끝에 붙어있는 다중 세그먼트를 표현하는데 사용된다.
  • 터틀 그래픽스의 스택 상태가 사용된다.(push와 pop을 위해 꺽쇠를 사용한다.)
  • 터틀 그래픽스에서 최종 문자열로 가는 과정이 이산적인 사건의 식물 성장을 표현한다.
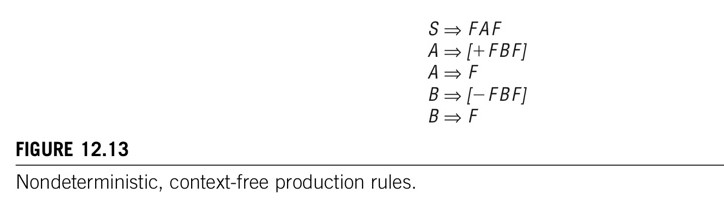
  • 생성 규칙은 문맥-자유이며 비결정적(nondeterministic)이다.(Figure 12.13)
  • 더욱 그럴듯한 애니메이션을 만들기 위해서는 점진적인 외형 변화와 이에 따른 길이 변화를 잘 보여주는 방법이 필요하다.

• 확률적(Stochastic) L-System
  • 왼편의 합이 1이 되는 사용자가 정의한 확률을 각 생산물에 할당한다. (Figure 12.16)
  • 확률적 L-System을 사용하여, 일정한 군집성과 같은 유사도를 보여주는 넓은 범위의 분기구조를 가지도록 할 수 있다.

• 문맥-자유 vs 문맥-인식
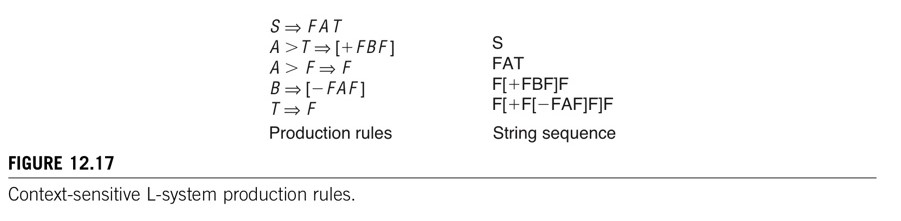
  • 문맥-인식 L-System은 기호가 나타내는 문맥의 앞 뒤 상황에 따라 서로 다른 문자열이 생성된다. (Figure 12.17)

12.2.3 Animating Plant Growth

• 식물의 애니메이션 유형
  • 유연성 있는 움직임
  • 고정된 구조를 가짐
• 성장 과정의 두 측면
  • 성장 과정에서 나타나는 위상의 변화
    • 시간에 따른 이산적인 사건
    • 분기 구조를 캡슐화하는 생산물의 형태로 모델링 된다.(A=>F[+F]B와 같은 형태)
  • 현재 구조의 변형률(elongation)
    • F=>FF와 같은 형식의 생성 규칙에 따라 모델링된다.
• Parametric L-Systems
  • 기호와 관련있는 한 개 이상의 보조변수(parameter)를 가질 수 있다.
  • 보조 변수들은 L-System의 생성물에 의하여 설정되고 모델링 된다.
• Timed L-Systems
  • 모든 생성물에 접근 가능하며 문자열의 진화를 제어하는데 도움을 주는 전역 시간 변수와 모든 문자와 관련있는 지역 경과 값 두가지의 개념을 더한다.
  • 시간성 생성물은 시간이 흘러 기호가 가지고 있는 일정한 종료 시간에 도달하면 대응되는 기호에 적용할 수 있다.
• Interacting with the Environment
  • 주변환경(물리적 방해, 일사량, 중력, 바람 등)은 다양한 방식으로 식물의 성장에 영향을 준다.
  • 환경과 양방향으로 작용하는 식물의 모델링과 애니메이션 틀을 사용하는 방식
    • 통신 항목을 이용하여 외부 환경으로 정보를 전달하고 정보를 요청하는 개방형 L-System을 사용한다.
    • 식물의 모델의 상태는 환경 정보의 결과에 영향을 주며 새로운 식물의 가지를 제어하는 비율을 변화시킨다.

12.3 Subdivision Surface

• 분할 곡면은 하향식 방법으로 객체를 설계하는 애니메이션에서 유용하다.
• 각 단계는 모서리와 가장자리를 다듬어서 보통 객체의 복잡성을 더한다.
• 분할을 하는동안 각 정점은 면으로 대체된다.