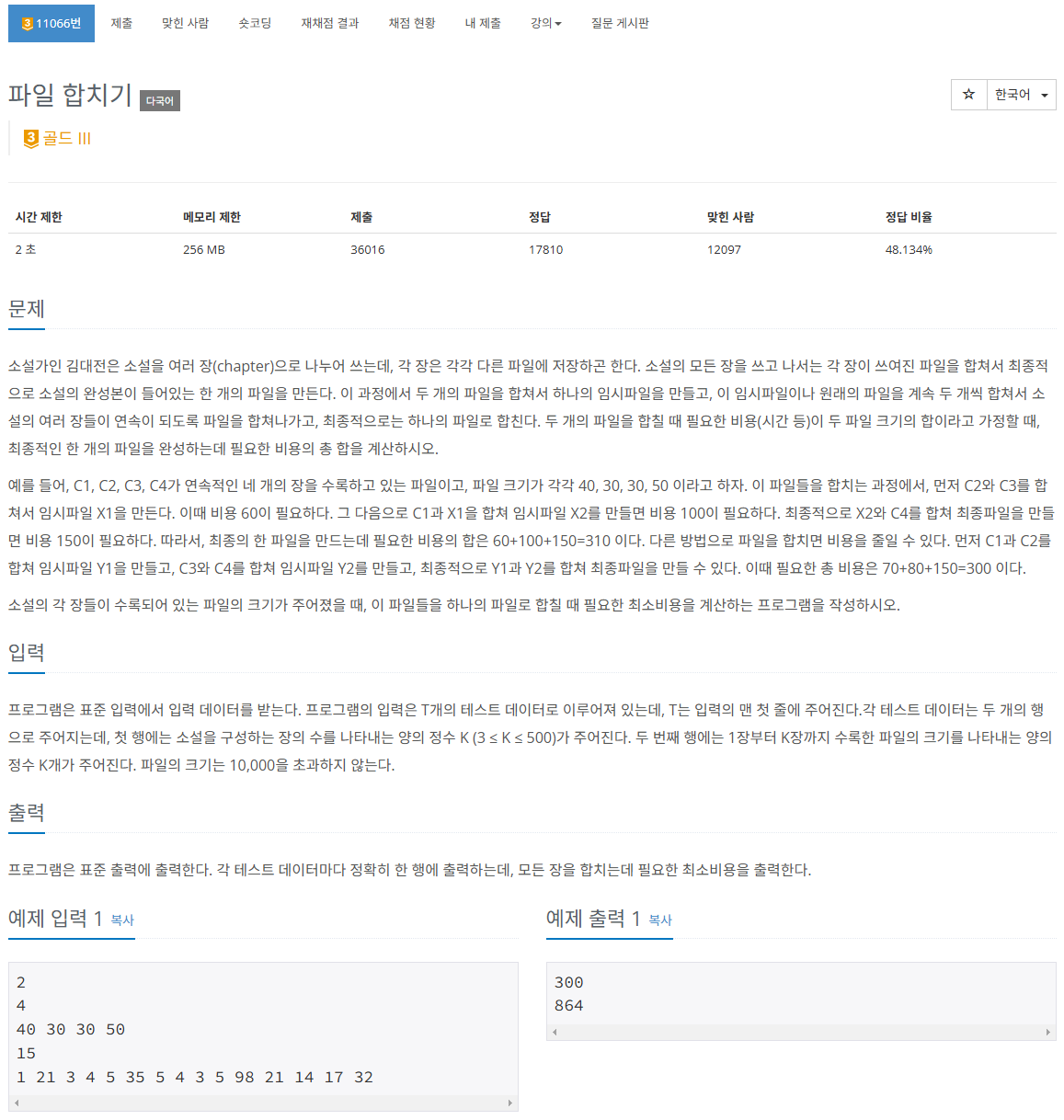
문제 해석
-
일단, 왜 DP로 풀어야 하는가에 대해서 설명하자면
-
C1, C2, C3, C4가 있을 때 모두 더한다고 해보자. (더하는 순서는 다를 수 있음)
-
경우의 수는 아래와 같이 나올 수 있다.
- ((C1+C2)+C3)+C4
- (C1+C2)+(C3+C4)
- C1+(C2+ (C3+C4))
- C1+((C2+C3)+C4)
- (C1+(C2+C3))+C4
-
위와 같이 색깔위주로 봤을 때 중복된 연산이 존재한다.
-
중복된 연산을 제거해야 빨라지는데 그렇다면 어떻게 제거하면 될까? 답은 중복된 연산을 제거하기 위해 계산된 연산은 저장하면된다(=메모리제이션)
-
즉, 동적프로그래밍을 사용해야한다는 뜻이다
-
이제 본론으로 이 문제를 풀기 위해서는 중복된 연산은 저장하고 누적합을 통해 최소비용을 뽑아내야 한다.
-
이 문제의 예시처럼 C1(40), C2(30), C3(30), C4(50)인 경우로 설명을 하고자 한다.
-
문제풀이를 설명하기 앞서 DP 2차원 배열을 만들건데 몇가지 알고 가야하는 것이 있다.
- 이웃한 장끼리만 더할 수 있다.
ex. C1+C3 이런식으로 더할 수 없다는 뜻 - 아래 표와 같이 행은 시작점을 의미하고 열은 끝점을 의미한다.
dp[K][K] 배열 (K=3)
1 2 3
a b c
1 a 0 a~b a~c
2 b 0 b~c
3 c 0
- 이러한 특징으로 a~c의 총 합은 dp[1][3]라고 볼 수 있다.
- 열이 K가 n일때 1~K의 총 합은 dp[1][K]
- 자신과 자신을 더하는 건 더할 수 있는 게 없기 때문에 0으로 지정한다.(시작과 끝이 같기 때문에 비용이 안든다!)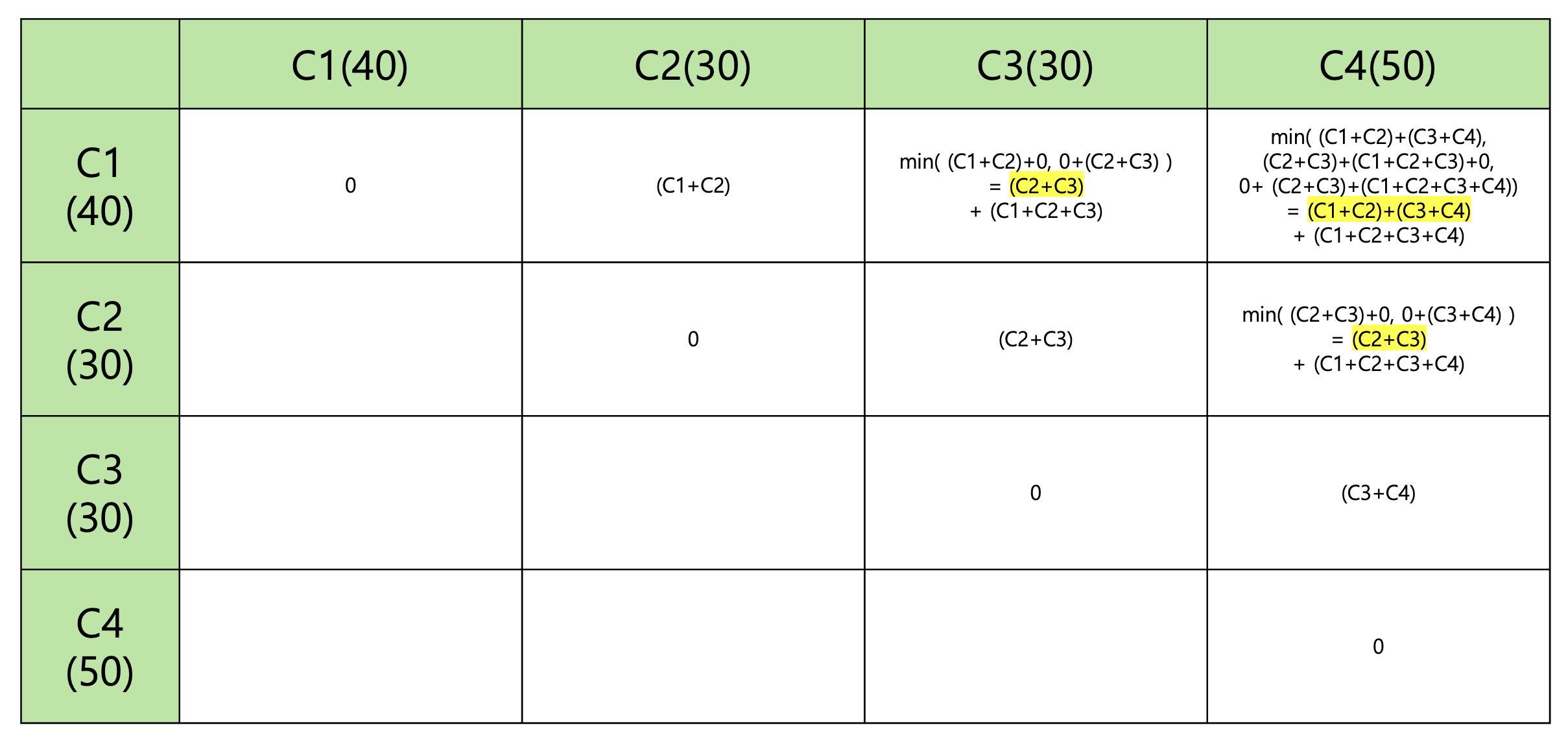
좀 더 이해를 돕기 위해 C1~C3의 최소비용을 구해보자.
(C1+C2)+0(=C3) 와 0(=C1)+(C2+C3) 중 최솟값 (C2+C3) = 60에
누적합 (C1+C2+C3) = 100 인 160이 된다.
더 보자면 C1~C4의 최소비용을 구해보자
(C1+C2)+(C3+C4) 와
0(=C1)+(C2+C3)+(C1+C2+C3+C4) 와
(C2+C3)+(C1+C2+C3)+0(=C4) 중 최솟값안 (C1+C2)+(C3+C4) = 150에
C1~C4의 누적합인 (C1+C2+C3+C4) = 150을 더한 300의 최소금액을 구한다.
여기 풀이에서 보듯이 마지막에 더하는 누적합은 고정이고
dp[시작점][끝점] : 시작점~끝점의 파일들을 합치는데 필요한 비용만 바뀌기 때문에 dp[시작점][끝점]의 최솟값을 찾으면 된다!
- 위의 풀이 방식대로 구하면 값은 아래와 같고, 결국 C1~C4의 최소비용은 인덱스가 1부터 시작한다 했을때 1번째 행의 4번째 열인 값이 최소비용이 된다. (모두 수행한 후의 값)
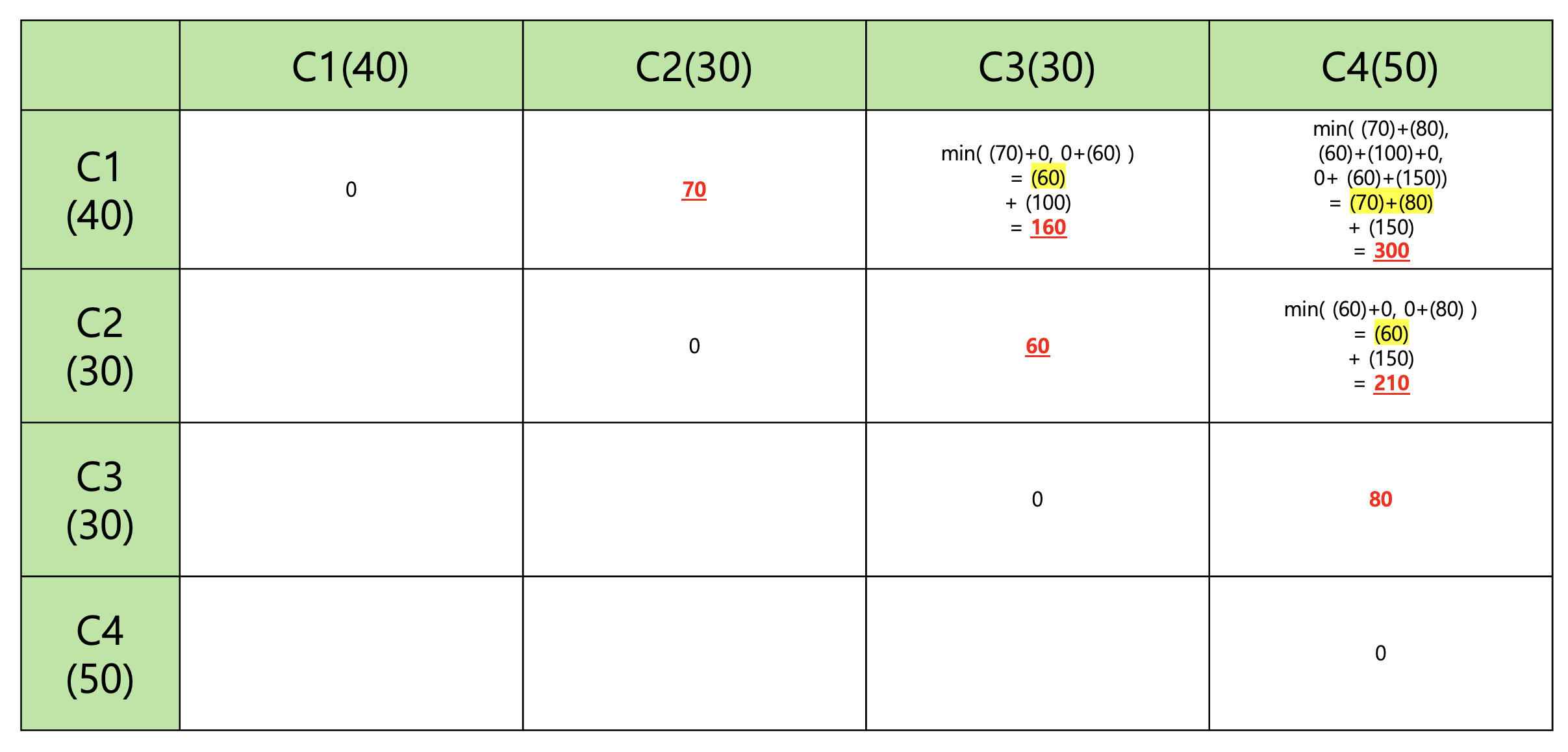
- 그외의 설명은 주석으로 작성해두었다.
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine()); //테스트 데이터 개수
while(T --> 0){ //테스트 데이터 개수만큼 반복
int K = Integer.parseInt(br.readLine()); //장의 개수
st = new StringTokenizer(br.readLine()); //수록한 파일의 크기를 입력
int[] sum = new int[K+1];
int[][] dp = new int[K+1][K+1]; //동적 계획법 사용시
for(int i = 1; i <= K; i++){
/* 누적합을 사용하는 게 더 효율적이다.
누적합이 아닌 본래 입력값을 사용하게 되면 범위에 있는 파일크기 개수만큼 더하는 연산을 진행해줘야하기 때문에
특정범위값을 구할 땐 끝점에서 - (시작점-1)을 하면 구할 수 있다.
=> 파일크기 개수만큼 연산이 늘지 않고 항상 일정한 연산을 수행할 수 있음
*/
sum[i] = sum[i-1]+ Integer.parseInt(st.nextToken()); //장의 개수만큼 수록된 파일의 크기를 입력
}
for(int page = 1; page <= K; page++){ //연산(+)의 개수 : (page+1)장씩 붙인다
for(int start = 1; start+page<= K; start++){ //시작 점 : 붙이기 시작하는 점
int end = start+page; //끝 점 : 붙이는 걸 끝내는 점
dp[start][end] = Integer.MAX_VALUE; //최솟값을 구하기 위해 정수(int) 가장 큰 값으로 초기화
for(int cut = start; cut < end; cut++){ //자르는 점 : 시작점과 끝점 사이에 자르는 점
dp[start][end] = Math.min(dp[start][end], dp[start][cut] + dp[cut+1][end] + (sum[end] - sum[start-1]));
}
}
}
sb.append(dp[1][K]).append("\n"); //1번째부터 K번째의 누적합 부분이 최종이면서 최소의 비용 값
}
br.close();
System.out.println(sb);
}
}결과

느낀 점
개인적으로 이 문제는 정말 너무 어려웠다. 동적계획법1을 풀때도 어렵게 느꼈었는데 오랜만에 다시 접하니까 '아... 맞다 어렵게 생각한 문제였지... 잊고 있었네...' 라고 생각을 했다. 2일을 걸려서 이 문제를 이해하고 풀어냈던 것 같다. (물론 다른 분들이 작성하신 설명이나 코드들을 봐가면서... 특히 문제자체를 이해하고자...)
참조한 블로그1, 참조한 블로그2
어찌저찌 풀긴 했지만 아직 동적프로그래밍은 많이 부족한 것 같다...
그리고 이 문제의 카테고리가 동적계획법2에 해당하는 문제라 당연히 동적프로그래밍을 사용해야하는 문제라고 자연스럽게 생각할 수 있지만 카테고리가 없으면 사실 어떤 방식으로 풀어야하는지 감이 안잡히겠다는 생각이 들었다. 그래서 처음으로 '왜 이 문제를 동적프로그래밍으로 푸는 것이 효율적인가?'에 대해 써보았지만 아직은 카테고리가 없으면 어려울 것 같다...
