백준 11049 행렬 곱셈 순서[JAVA]

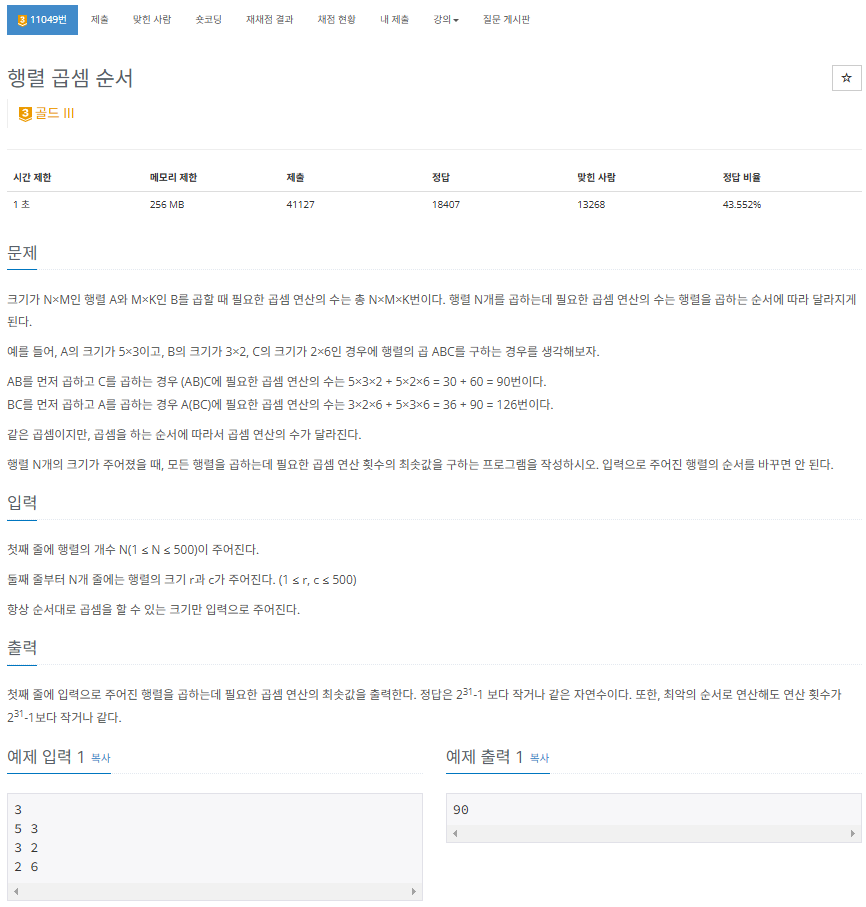
문제 해석

• 행렬의 개수(N)을 입력받고 입력받은 행렬을 모두 곱셈했을 때 곱셈은 총 몇번하는지 구하는 문제이다.

• 단 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.

  • 즉, 이웃한 행렬끼리 곱셈을 할 수 있다. (서로 떨어진 행렬은 안됨)
    • 이웃한 행렬끼리만 곱할 수 있다는 특징으로 많은 경우의 수가 줄 수 있음 (순서를 섞어보면서 구하지 않아도 되기 때문)

• 첫번재 줄에 행렬의 개수를 입력받고, 두번째 줄부터 +N개의 줄까지 행렬의 크기(행(r) 열(c)) 입력받는다.

• 문제에서 나온 예제로 행렬곱셈을 어떻게 다이나믹 프로그래밍을 적용해서 푸는지 설명하고자 한다. (아래 참고)

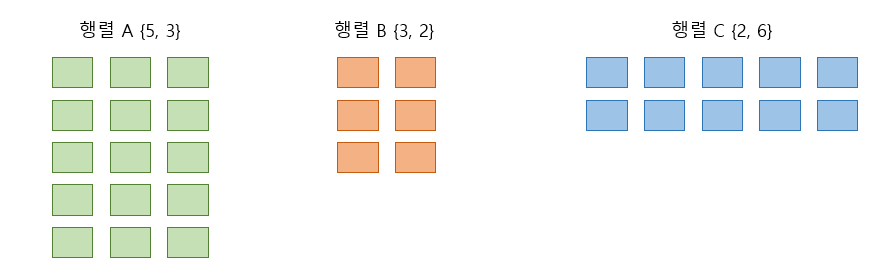
• 행렬이 아래와 같이 존재한다. (우리가 구할려는 것은 최소곱셈 횟수만 구하면 되므로 도형으로 나타내보았다.)
  

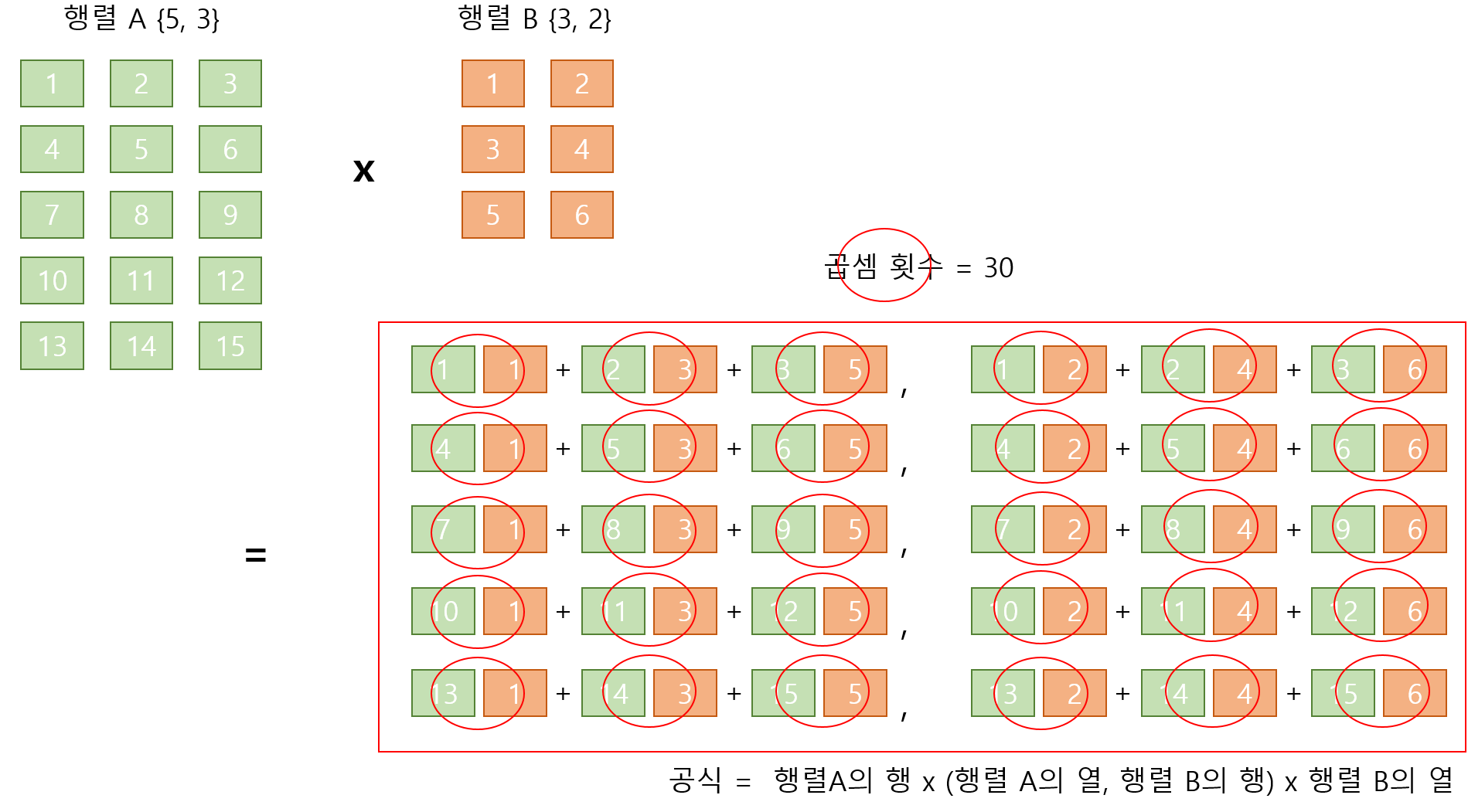
• 여기서 잠깐 행렬의 곱셈은 어떻게 진행되는지 짚고 넘어가자면
  

• 백준에 나온 예시로 행렬 곱셈을 진행한다면 아래와 같이 진행될 것이다.
  

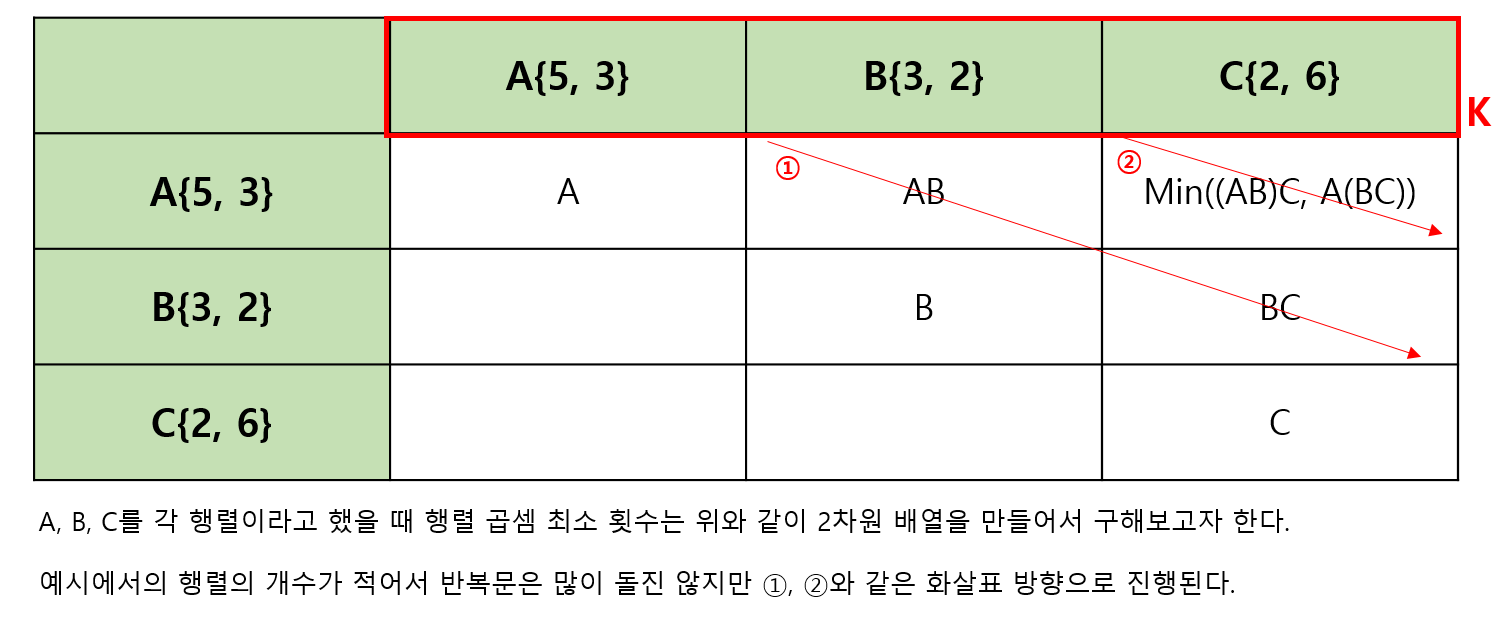
진행 절차는 아래와 같다.
(dp 배열 요소에 값이 없으면 0이다. 하지만 좀 더 보기 편하게 X로 표시해두었다.)

dp 			step1		step2		step3			step4
	X	X	X	 X	30	X 	 X	30	 X 	X	30	126		X	30	90
	X	X	X	 X	X	X	 X	 X  36	X	 X	 36		X	 X	36	
	X	X	X	 X	X	X	 X	 X	 X	X	 X	  X		X	 X	 X
	
	반복문 1) k = 1
		반복문 2) i = 0
			반복문 3) j = 0 (step1)
				* dp[0][1] = Math.min(dp[0][1], dp[0][0] + dp[1][1] + matrixs[0][0]*matrixs[0][1]*matrixs[1][1]
					dp[0][0] = 0
					dp[1][1] = 0
					matrix[0][0] = 5
					matrix[0][1] = 3
					matrix[1][1] = 2
					=> 5*3*2 = 30
		반복문 2) i = 1
			반복문 3) j = 1 (step2)
				* dp[1][2] = Math.min(dp[1][2], dp[1][1] + dp[2][2] + matrixs[1][0]*matrixs[1][1]*matrixs[2][1])
					dp[1][1] = 0
					dp[2][2] = 0
					matrixs[1][0] = 3
					matrixs[1][1] = 2
					matrixs[2][1] = 6
					=> 3*2*6 = 36
	
	반복문 1) k = 2
		반복문 2) i = 0
			반복문 3) j = 0 (step3)
				*dp[0][2] = Math.min(dp[0][2], dp[0][0]+dp[1][2]+matrixs[0][0]*matrixs[0][1]*matrixs[2][1])
					dp[0][2] = 0
					dp[0][0] = 0
					dp[1][2] = 36
					matrixs[0][0] = 5
					matrix[0][1] = 3
					matrixs[2][1] = 6
					=>36+(5*3*6) = 126
			반복문 3) j = 1 (step4)
				*dp[0][2] = Math.min(dp[0][2], dp[0][1]+dp[2][2]+matrixs[0][0]*matrixs[1][1]*matrixs[2][1])
					dp[0][2] = 136
					dp[0][1] = 30
					dp[2][2] = 0
					matrixs[0][0] = 5
					matrixs[1][1] = 2
					matrixs[2][1] = 6
					Math.min(136, 30+(5*2*6)) = Math.min(136, 90) = 90
					
	* dp[0][2]라는 의미는 0~2까지의 행렬(A행렬~C행렬) 모두 곱한 값을 의미한다.
    => 즉, dp[0][2] = 90 (최솟값)이 된다.

• 이 문제의 Kick

	for(int k = 1; k < N; k++){
		for(int i = 0; i+k < N; i++){
        	//설정 안하면 값이 갱신이 안됨
            //값이 없는 경우 정수의 최댓값으로 초기화하여 최솟값을 찾기
			dp[i][i+k] = Integer.MAX_VALUE; 
			for(int j = i; j < i+k; j++){
				dp[i][i+k] = Math.min(dp[i][i+k], dp[i][j]+dp[j+1][i+k]
							+matrixs[i][0]*matrixs[j][1]*matrixs[i+k][1]);
			}
		}
	}

코드

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        int N = Integer.parseInt(br.readLine()); //행렬의 개수
        int[][] matrixs = new int[N][2]; //행렬 크기 저장하는 배열
        int[][] dp = new int[N][N]; //행렬의 곱셈연산 횟수를 저장하는 배열

        //입력 순서 (행렬의 크기 행(r) x 열(c))
        for(int i = 0; i < N; i++){
            st = new StringTokenizer(br.readLine());
            matrixs[i][0] = Integer.parseInt(st.nextToken()); //행 크기
            matrixs[i][1] = Integer.parseInt(st.nextToken()); //열 크기
        }

        br.close();

        for(int k = 1; k < N; k++){
            for(int i = 0; i+k < N; i++){
                dp[i][i+k] = Integer.MAX_VALUE; //초기값은 일단 가장 큰 값으로 저장
                for(int j = i ; j < i+k; j++){
                    dp[i][i+k] = Math.min(dp[i][i+k], dp[i][j]+dp[j+1][i+k] + matrixs[i][0]*matrixs[j][1]*matrixs[i+k][1]);
                }
            }
        }

        System.out.println(dp[0][N-1]);

    }

}

결과

느낀 점

오래 걸려서 풀었던 문제로 분명 유사한 문제를 많이 풀었음에도 이해하는데 오래 걸렸다...
다이나믹 프로그래밍 진짜 너무 어려운 것 같다. (행렬 곱셈,,,)