최소 신장 트리 (MST)

1. 신장 트리 (Spanning Tree)

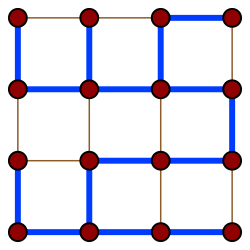
무방향 그래프에서 모든 정점을 포함하며, 사이클이 없는 부분 그래프

위 그림에서 파란색으로 색칠된 부분이 신장 트리 (출처)

2. 최소 신장 트리 (Minimum Spanning Tree)

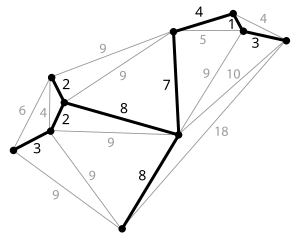
위에서 살펴본 신장 트리중에서 간선의 가중치의 합이 최소가 되는 트리

위 그림에서 검은색으로 색칠된 부분이 최소 신장 트리 (출처)

3. MST를 생성하는 알고리즘

1) Kruskal

유니온 파인드 자료구조를 활용한 MST생성

• 가중치가 최소인 간선을 선택
• 해당 간선을 연결해도 사이클이 형성되지 않을 경우에 연결
  • 여기서 Union Find을 통해서 사이클 여부를 확인할 수 있음.
    • 해당 간선의 목표인 정점들의 부모가 같다 -> 이미 연결 되어있다 -> 이 간선을 연결하면 사이클이 형성된다
    • Union 연산에서 두 정점의 부모가 다를때만 합치기

int Find(int x)
{
    if (parents[x] == x)
        return (x);
    return Find(parents[x]);
}

void Union(int a, int b, int& answer, int& cost) 
{
    int A = Find(a);
    int B = Find(b);

    if (A!=B)
    {
        if (A < B) 
            parents[B] = A;
        else 
            parents[A] = B;
        answer += cost;
    }
}

2) Prim

임의의 정점에서 시작해 MST를 구성하는 방법

• 1. 임의의 정점 선택
• 2. 해당 정점(들)과 이어진 간선의 가중치중 최소 값을 가진 간선 선택
• 3. 위에서 결정된 정점 신장 트리에 추가
• 모든 정점이 추가될 때까지 2,3 반복

#include <string>
#include <vector>
#include <unordered_set>
#include <queue>

using namespace std;

struct ComaparePair
{
    bool operator()(pair<int, int> a, pair<int, int> b)
    {
        // 누가 우선순위가 높은지
        // true인 경우 b가 a보다 우선순위가 높음
        return a.second > b.second;
    }
};

int solution(int n, vector<vector<int>> costs) {
    int answer = 0;
    vector<vector<pair<int, int>>> edges(100);
    priority_queue<pair<int,int>, vector<pair<int, int>>, ComaparePair> pq;
    unordered_set<int> mst;

    for(int i = 0; i < costs.size(); ++i)
    {
        int from = costs[i][0];
        int to = costs[i][1];
        int cost = costs[i][2];
        edges[from].push_back({to, cost});
        edges[to].push_back({from, cost});
    }

    pq.push({0,0});

    while(mst.size() < n)
    {
        int current_node = pq.top().first;
        int current_cost = pq.top().second;
        pq.pop();

        if (mst.count(current_node) != 0) continue;

        mst.insert(current_node);
        answer += current_cost;

        for (int i = 0; i < edges[current_node].size(); ++i)
        {
            int next_node = edges[current_node][i].first;
            int next_cost = edges[current_node][i].second;
            if (mst.count(next_node == 0))
                pq.push({next_node, next_cost});
        }
    }
    return answer;
}