Data Science - Monty Hall Problem

이번 글에선 다들 한번쯤은 들어봤을만한? 흥미로운 문제를 하나 들고왔다.
바로 몬티홀 문제다. 이거는 아마 고등학교 확률과 통계를 열심히 공부한 사람이면 기억나는 문제일 것이다. 그래서 이번 글에선 이 몬티홀 문제를 가지고 통계적 측면에서 접근해볼 예정이다. 그럼, 시작.

Monty Hall Problem

우선 그래도 혹시나 모르거나 까먹은 분들을 위해서 설명해주겠다.

몬티홀 문제는 캐나다-미국 TV 프로그램 사회자가 진행하던 미국 오락 프로그램 《Let's Make a Deal》에서 유래한 확률 문제다. 게임 룰을 간단 요약하자면

1. 3개의 문이 있고, 3개 중 2개의 문에는 염소가 있고, 나머지 하나의 문에는 차가 들어있다.
2. 참가자(Contestant)가 3개의 문 중 하나를 고른다.
3. 사회자는 참가자가 고르지 않은 2개의 문중 염소가 있는 1개의 문을 연다.
4. 사회자는 참가자에게 자신의 선택을 바꿀 기회를 주고, 바꿀지 말지 선택의 기회를 준다.

한마디로 인생한방(?) 게임이다. (나도 참가하고 싶다.)

결론은, 참가자는 총 2가지의 선택을 할 수 있다.
1. 처음 선택한 문
2. 나머지 선택하지 않은 미공개된 1개의 문

그래서 이번 글은!!! 몬티홀 문제를 통계적 수치를 통해 비교함으로서 어떤 선택이 좀더 확률적으로 자동차가 나올 문을 열 수 있을지 알아보자.

Let's play with code,,

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

doors = ['Car', 'Goat 1', 'Goat 2']
goats = ['Goat 1', 'Goat 2']

우선 저번 시간까지 지긋지긋하게 썼던

import pandas as pd
import numpy as np

이 두개의 선언문은 이제 익숙할 것이다 그러나

import matplotlib.pyplot as plt

이거는 생소할 수도 있다.
이 'matplotlib.pyplot' 라이브러리는

matplotlib의 pyplot 모듈을 가져와서 plt라는 별칭으로 사용하겠다는 의미다.
주로 파이썬에서 데이터를 차트나 플롯으로 시각화하기 위해 사용되곤 한다.
아마 앞으로 Pandas를 다룰 떄마다 pandas,numpy와 함께 자주 사용될 것이다.

그래서 이렇게 라이브러리를 선언해주고

doors = ['Car', 'Goat 1', 'Goat 2']
goats = ['Goat 1', 'Goat 2']

이렇게 Array까지 선언해주면 초기 준비단계는 작업 완료다.

def other_one(x, a_b):
  if x == a_b[0]:
    return a_b[1]
  elif x == a_b[1]:
    return a_b[0]
  else:
    return 'Input Not Valid'

다음은 def를 통해 other_one이란 함수를 만든다.
아마 코딩에 익숙한 분들은 단번에 구조를 알아차릴 수 있다.

함수인자로 선언한(x, a_b[])를 서로 비교하면서 같은 값들이 있으면 a_b[]의 값을 return해주고 같은 값들이 없으면 'Input Not Valid'를 return해준다.

original = 'Goat 1'
outcome = [original, other_one(original, goats), 'Car']
outcome

['Goat 1', 'Goat 2', 'Car']

original = 'Goat 2'
outcome = [original, other_one(original, goats), 'Car']
outcome

['Goat 2', 'Goat 1', 'Car']

original = 'Car'
throw_out = np.random.choice(goats)
outcome = [original, throw_out, other_one(throw_out, goats)]
outcome

['Car', 'Goat 2', 'Goat 1']

위의 3개의 코드는 한꺼번에 설명하자면 3가지 경우의 수를 둔 것이다.
outcome, 즉 결과값으로 생성될 list를 3개로 쪼개서 생성하는 것이다.
이때 앞에서 정의한 other_one 함수를 사용해서 list를 생성하는 것이 핵심 point.

특히 마지막 list의 첫번째 원소를 'Car'로 설정하는 부분을 뜯어보면
throw_out이란 변수를 설정해서 나머지 원소로서 들어갈 'Goat 1', 'Goat 2' 를 np.random.choice를 통해 무작위로 들어가게끔 한다.

참고로 original이란 변수는 참가자가 처음으로 선택한 문이라고 생각하면 된다.

"""
  Check whether the name of a door (a string) is a Goat.
  Examples:
  =========
  >>> is_goat('Goat 1')
  True
  >>> is_goat('Goat 2')
  True
  >>> is_goat('Car')
  False
"""

def is_goat(door_name):
  if door_name == "Goat 1":
    return True
  elif door_name == "Goat 2":
    return True
  else:
    return False


"""
  Play the Monty Hall game once
  and return an array of three strings:
  original choice, what Monty throws out, what remains
"""

def monty_hall():
  original = np.random.choice(doors)
  if is_goat(original):
    return [original, other_one(original, goats),'Car']
  else:
    throw_out = np.random.choice(goats)
  return [original, throw_out, other_one(throw_out, goats)]

자 이것도 살펴보면 is_goat()라는 함수를 통해서 선택한 문이 Goat인지 Car인지를 True,False를 통해 구분하게 한다.

마찬가지로, monty_hall()이란 함수를 통해서 전에 생성한 list의 original이 무엇인지 파악하는 함수다.

# Number of times we'll play the game
N = 10000

original = []
throw_out = []
remains = []

for i in np.arange(N):
  result = monty_hall() # the result of one game
  # Collect the results in the appropriate arrays
  original = np.append(original, result[0])
  throw_out = np.append(throw_out, result[1])
  remains = np.append(remains, result[2])
# The for-loop is done! Now put all the arrays together in a # table.


df = pd.DataFrame({
    '<Original Door Choice>': original,
    '<Monty Throws Out>': throw_out,
    '<Remaining Door>': remains
})
print(df)

     <Original Door Choice> <Monty Throws Out> <Remaining Door>
0                    Goat 2             Goat 1              Car
1                       Car             Goat 1           Goat 2
2                    Goat 2             Goat 1              Car
3                       Car             Goat 2           Goat 1
4                    Goat 2             Goat 1              Car
...                     ...                ...              ...
9995                    Car             Goat 2           Goat 1
9996                 Goat 1             Goat 2              Car
9997                    Car             Goat 1           Goat 2
9998                 Goat 2             Goat 1              Car
9999                    Car             Goat 2           Goat 1

[10000 rows x 3 columns]

본격적으로 이때까지 만든 함수를 가지고 몬티홀의 경우의 수를 생성해볼려고 한다. N = 10000으로 설정한건 무려 10000번의 경우의 수를 생성한다고 보면 된다. 그렇게 해야지 좀더 정확한 통계값을 얻을 수 있기 때문!!

일단 세 개의 빈 리스트 original, throw_out, remains를 초기화한 뒤
각각의 리스트에 맞게 게임의 각 시뮬레이션 결과를 저장한다

그리고 DataFrame를 만들어서 무작위로 생성된 Result list를 그 안에 집어 넣는다.

rst = df['<Original Door Choice>'].unique()
rst

array(['Goat 1', 'Goat 2', 'Car'], dtype=object)

' 열에서 고유한 값을 추출하는 함수다. 그래서 참가자가 처음 선택한 문의 종류가 무엇이 있는지 확인하는 것이다. 당연히 10000번이나 실행했으므로 Goat 1, Goat 2, Car는 다 나올 것이다.

results_o = df['<Original Door Choice>'].value_counts()
results_o

Car       3353
Goat 1    3339
Goat 2    3308
Name: <Original Door Choice>, dtype: int64

자 그래서 어쩌면 핵심적인 부분일수도 있다. 바로 'Car', 'Goat 1', 'Goat 2'가 처음 선택한 문, 즉 'Original Door Choice'로 몇 번 등장했는지 counting을 해주는 코드다.

df[].value_count()를 통해서 해당 열에 맞는 값들이 몇 번 나왔는지 counting해준다.

results_r = df['<Remaining Door>'].value_counts()
print(results_r)

Car       6606
Goat 1    1697
Goat 2    1697
Name: <Remaining Door>, dtype: int64

여기서 조금 흥미로운 결과가 있다. 바로 전에 했던 count를 하는 함수를 'Remaining Door'에다가 실행시켰더니, 'Car'가 상당수를 차지한다.
굉장히 흥미로운 부분이다.

df = pd.concat([results_o, results_r], axis=1)

자 그래서 좀 더 흥미로운 부분을 찾아내기 위해서 우리는 pd.concat()이란 함수를 통해서 result_o(처음 선택한 문)과 result_r(남아있는 문)의 DataFrame을 서로 연결해서 살펴보도록 하겠다.

참고로 마지막에 'axis = 1'은 두 개의 DataFrame를 가로방향으로 연결한다는 뜻이다. 만약 1이 아니고 0이였으면 세로겠지?

_df = pd.DataFrame(df,columns=['<Remaining Door>', '<Original Door Choice>'], index = ['Goat 2', 'Goat 1', 'Car'])
# Multiple horizontal bar chart
_df.plot.barh()

# Display the plot
plt.show()

자 그래서 두개가 합쳐서 된 하나의 DataFrame인 _df을 생성하고

plot.barh()를 통해서 Multiple horizontal bar chart, 즉 수평 막대 차트를 생성한다. 그러면 어떤 결과가 나오냐고?

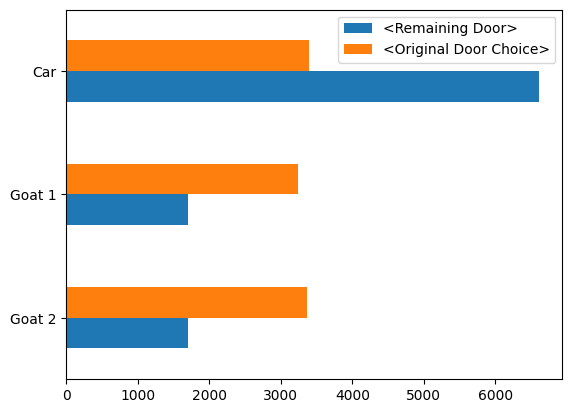
이런 결과가 나온다 'Car', 'Goat 1', 'Goat 2'가 Original Door Choice로는 비율이 거의 똑같이 나오는데 Remaining Door로 살펴보면 'Car'가 거의 압도적으로 나온다.

다른 종류의 그래프를 생성해서 또 알아보자

x = np.arange(3)
width = 0.40

# plot data in grouped manner of bar type
plt.bar(x-0.2, df['<Original Door Choice>'], width)
plt.bar(x+0.2, df['<Remaining Door>'], width)

위 함수들은 그냥 일반 막대 차트로 표시하되 따로 세부설정을 통해서 그래프를 구체화시킨다.

코드를 자세히 뜯어보면, x-0.2, x+0.2와 width가 눈에 띌 것이다. 이거는 막대의 위치를 조정하면서 width를 0.40으로 설정하게 한다. 그렇게 설정하면 결과가 어떻게 나오냐고?

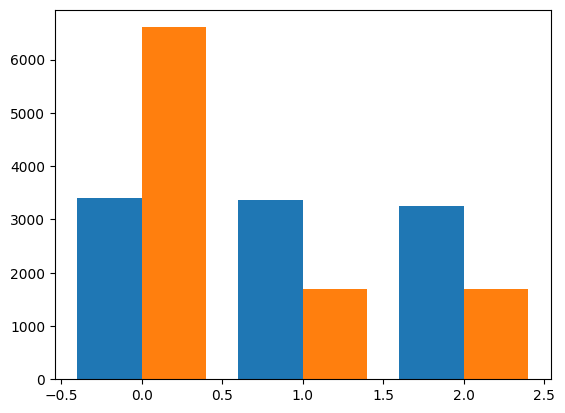
이렇게 나온다. 자 이렇게 다양한 chart를 생성하면서 Monty hall 문제를 통계적으로 살펴보았다. 그래서 Remaining Door에 'Car'가 압도적으로 많이 뜬걸 보고 무엇을 알 수 있냐고?

'몬티홀 문제에선 선택을 바꾸는 게 이득이다'
라는 답이다. 하지만 남자는 뭐다? 한번 선택한거 그대로 밀고 가야지