
이번 글은 잘 이해가 안될 수도 있다. 벨로그를 쓰면서 배워가는 중이라 틀린 부분도 있을 수 있으니 피드백 환영한다. 그럼, 시작.
Empirical Distribution of a Statistic
자 이번 글을 본격적으로 작성하기에 앞서 Empirical Distribution(경험분포)에 대해서 알아보자
경험 분포는 쉽게 설명하자면 Randomly하게 Sample들을 추출해서 이를 바탕으로 분포를 측정해보는 것이다.
그런데 이러한 Empirical Distribution에는 특이한 법칙이 있다.
바로 "The Law of Averages"란 것인데, 대수의 법칙이라고도 부른다.
쉽게 설명하자면, 큰 수의 Sample을 추출한 경우, 그 표본의 평균이나 비율이 전체 모집단(population)의 평균과 비율과 유사하게 나온다는 뜻이다.
그럼 코드를 통해서 분석해볼까?
united = Table.read_table(path_data + 'united_summer2015.csv')delay_bins = np.arange(-20, 201, 10)
united.hist('Delay', bins=delay_bins, unit='minute')
plots.title('Population')이 코드들을 하나하나씩 뜯어보면 여지껏 보지못한 코드들이 있을 것이다.
Table.read_table 함수를 사용하여 데이터를 불러온다.
이 함수는 'datascience' 패키지의 Table 클래스에 속해있으므로
우리가 이제 선언문으로 작성해야될것으로 하나가 더 늘었다.
from datascience import *
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt (이제 pandas를 활용할땐 이렇게 기본으로 깔고 들어가자)
그리고 이제
delay_bins = np.arange(-20, 201, 10):
이 부분은 np.arrange 함수를 사용하여 -20에서 200까지 10의 간격으로 값을 생성하는 부분이다. 그래서 이렇게 선언한 부분을 밑에 활용하는 것이다.
united.hist('Delay', bins = delay_bins, unit = 'minute'):
united 테이블의 'Delay' 열에 대한 Histogram을 그리는 부분이다. 여기서 사용하는 bins는 위에서 정의한 delay_bins로, 지연 시간의 범위를 -20분에서 200분까지 10분 간격으로 나눈다.
unit = 'minute'는 x축의 단위를 '분'으로 설정한다.
plots.title('Population'):
Histogram의 제목을 'Population'으로 설정한다.
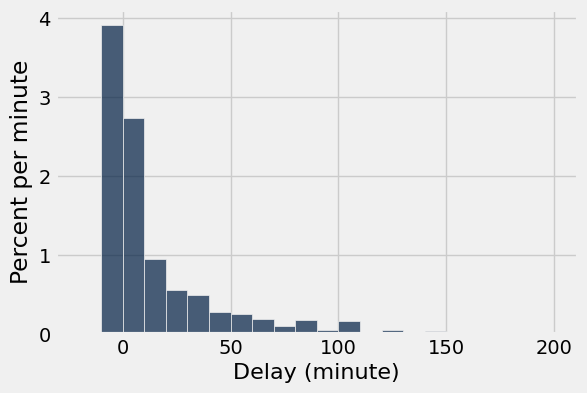
이렇게 코드를 짜고 실행하면 결과가 이렇게 나올 것이다.
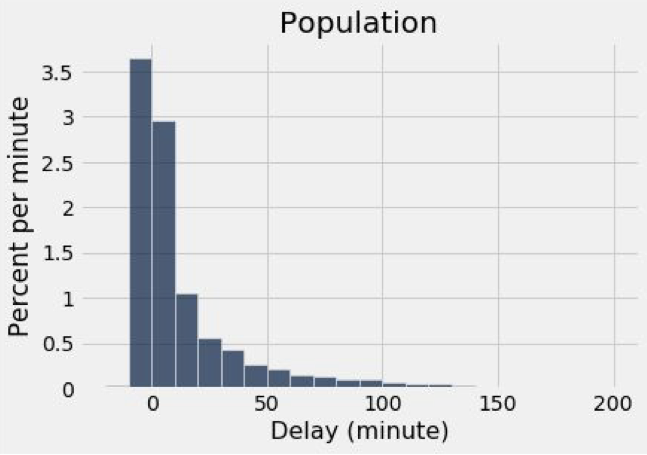
(기가 막히게 나왔다)
이 그래프가 모집단 즉, Population의 평균과 비율을 비교한 것이다.
그렇다면 임의의 Sample를 추출해서 비교를 해보자
코드는 위와 비슷하다.
sample_1000 = united.sample(1000)
sample_1000.hist('Delay', bins = delay_bins, unit = 'minute')
plots.title('Sample of Size 1000')이렇게 비슷하게 구성해보았다. 총 1000개의 표본을 생성하고 표본들의 평균과 비율을 구하는 Histogram를 결과로 보이게 했다. 그 결과는
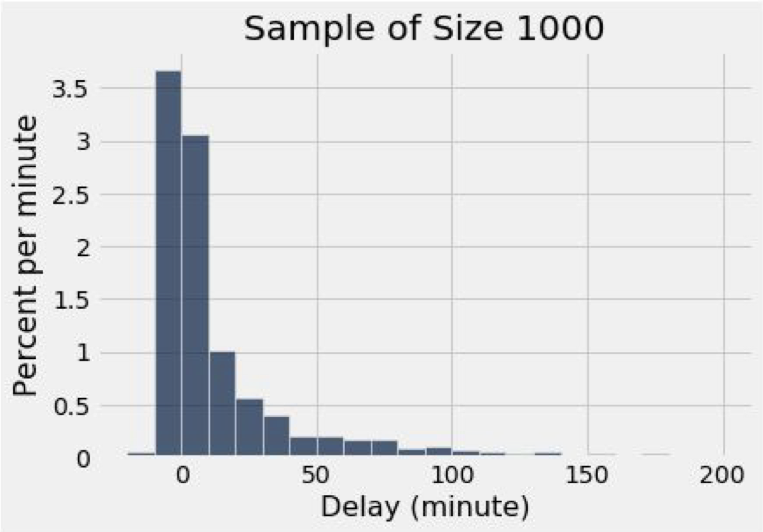
이렇다. 위의 Population 그래프와 상당히 비슷하지 않는가? 흥미롭다.
이렇게 'The Law of Averge', 대수의 법칙에 대해 알아보았다.
Parameter
parameter는 한국말로 번역하면 매개변수? 정도로 알면 된다.
통계학적 측면으로 살펴보자면, parameter는 population의 특성을 잘 나타내는 모수라고 알면 된다.
예를 들자면,
● 유권자 인구에서 A 후보에게 투표할 비율은?
● 페이스북 사용자 인구에서 사용자가 가장 많이 보유한 페이스북 친구 수는?
● 유나이티드 항공편의 모집단에서 출발 지연의 중앙값은?
이러한 Population과 관련된 모든 수치값들을 parameter라고 부른다.
그래서 우리는!! 저기 보이는 마지막 예시인 '유나이티드 항공편의 모집단'과 관련하여 코드를 분석해보겠다.
Statistic
통계치라고도 하는데, 이 통계치는 절대 고정적인 값이 될 수 없다. 왜냐?
Statistic은 ramdom sample을 기반으로 하기 때문에 다른 표본이 선택되어 Statistic를 나타낼 경우 다른 결과값이 나오기 때문이다.
그래서 여러 번의 Statistic 값을 비교 분석하면서 Check하는 것이 중요하다. 그렇다면 Statistic을 Simulating 하기 위한 절차에는 어떤 것이 있을까?
Simulating a Statistic
- simulate할 statistic를 결정한다.
- statistic 중 하나의 value를 return하는 함수를 작성한다.
예시를 보여주자면
def random_sample_median():
return np.median(united.sample(1000).column('Delay"))- 2단계를 얼마나 simulate할지 결정한다.
- simulate한 값들을 저장 및 관리하기 위해 Loop를 사용해서 array를 생성한다.
Visualization
시각화는 아까전에 위에 다뤘듯이 Histogram이나 plot를 이용해서 Visualization를 진행한다.
medians = make_array()
for i in np.arange(5000):
medians = np.append(medians, random_sample_median())simulated_medians.hist(bins=np.arange(0.5, 5, 1))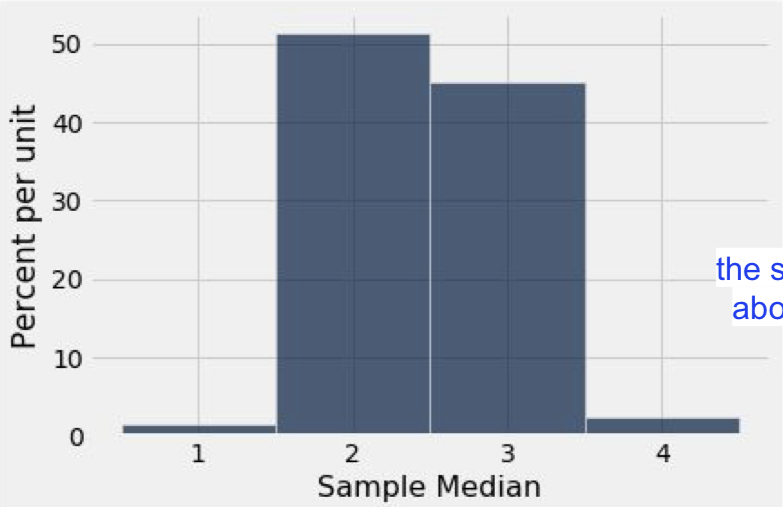
따라서 우리는, Visualization을 Sample의 크기에 따라 다르게 설정할 수 있다. 밑의 예시를 보자
Sample = 100일때
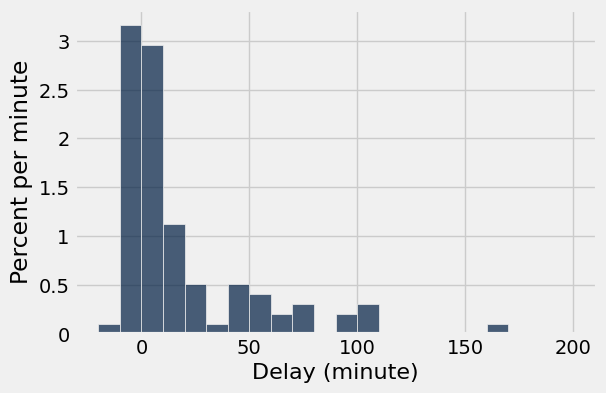
Sample = 1000일때
보시면 아시겠지만, 그래프의 모양이 비슷한데 Sample이 1000일때 뭔가 outlier가 없어진 느낌이다.
