문제

Given a sequence of integers, a1, a2, …, an, we define its sign matrix S such that, for 1 ≤ i ≤ j ≤ n, Sij="+" if ai + … + aj > 0; Sij="−" if ai + … + aj < 0; and Sij="0" otherwise.

For example, if (a1, a2, a3, a4)=( −1, 5, −4, 2), then its sign matrix S is a 4×4 matrix:

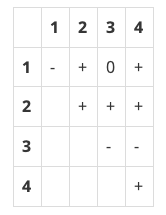
We say that the sequence (−1, 5, −4, 2) generates the sign matrix. A sign matrix is valid if it can be generated by a sequence of integers.

Given a sequence of integers, it is easy to compute its sign matrix. This problem is about the opposite direction: Given a valid sign matrix, find a sequence of integers that generates the sign matrix. Note that two or more different sequences of integers can generate the same sign matrix. For example, the sequence (−2, 5, −3, 1) generates the same sign matrix as the sequence (−1,5, −4,2).

Write a program that, given a valid sign matrix, can find a sequence of integers that generates the sign matrix. You may assume that every integer in a sequence is between −10 and 10, both inclusive.

입력

The first line contains an integer n(1 ≤ n ≤ 10), where n is the length of a sequence of integers. The second line contains a string of n(n+1)/2 characters such that the first n characters correspond to the first row of the sign matrix, the next n−1 characters to the second row, ..., and the last character to the n-th row.

출력

Output exactly one line containing a sequence of n integers which generates the sign matrix. If more than one sequence generates the sign matrix, you may output any one of them. Every integer in the sequence must be between −10 and 10, both inclusive.

예제1-입력

4
-+0++++--+

예제1 - 출력

-2 5 -3 1

예제2-입력

2
+++

예제2 - 출력

-2 5 -3 1

예제3-입력

5
++0+-+-+--+-+--

예제3 - 출력

1 2 -3 4 -5

출력값은 예시고 조건에 맞는 값 아무거나 출력하면 됨
(솔직히 뭐 이렇게 문제를 냈나 싶었음..)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int n;
    static char[][] matrix;
    static int[] result;
    static boolean isFirst = true;

    public static void main(String[] args) throws NumberFormatException, IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());

        char[] input = br.readLine().toCharArray();
        matrix = new char[n][n];

        int i = 0, j = 0;
        for (int idx = 0; idx < input.length; idx++) {
            matrix[i][j++] = input[idx];
            if (j > n - 1) {
                j = ++i;
            }
        }

        result = new int[n];
        find_sequence(0);
        br.close();
    }

    static void find_sequence(int cnt) {
        if (cnt == n) {
            for (int i = 0; i < n; i++) {
                System.out.print(result[i] + " ");
            }
            System.out.println();
            System.exit(0);
            return;
        }

        for (int i = -10; i <= 10; i++) {
            result[cnt] = i;
            if (checking(cnt)) {
                find_sequence(cnt + 1);
            }
        }
    }

    static boolean checking(int now) {
        int i, j;
        for (i = 0; i <= now; i++) {
            int sum = 0;
            for (j = i; j <= now; j++) {
                sum += result[j];
                
                if (matrix[i][j] == '+' && sum <= 0) {
                    return false;
                } else if (matrix[i][j] == '-' && sum >= 0) {
                    return false;
                } else if (matrix[i][j] == '0' && sum != 0) {
                    return false;
                }
            }
        }
        return true;
    }
}