3.2. Linear Regression Implementation from Scratch

3.2. Linear Regression Implementation from Scratch

이제 선형 회귀 분석의 핵심 아이디어를 이해했으니 코드의 실제 구현을 통해 작업을 시작할 수 있다. 이 섹션에서는 데이터 파이프라인, 모델, 손실 함수 및 미니배치 확률적 그레이디언트 강하 옵티마이저를 포함한 전체 방법을 처음부터 구현한다. 현대의 딥 러닝 프레임워크는 거의 모든 작업을 자동화할 수 있지만, 처음부터 무언가를 구현하는 것이 여러분이 실제로 무엇을 하고 있는지 확실히 알 수 있는 유일한 방법이다. 또한 모델을 사용자 정의하고, 자체 레이어 또는 손실 함수를 정의할 때가 되면, 아래에서 작동하는 방식을 이해하는 것이 유용할 것이다. 이 섹션에서는 텐서와 자동 차별화에만 집중한다. 이후 딥 러닝 프레임워크의 부가기능을 활용하여 보다 간결한 구현을 소개할 것이다.

%matplotlib inline
import random
import torch
from d2l import torch as d2l

3.2.1. Generating the Dataset

단순하게 하기 위해, 우리는 부가 노이즈가 있는 선형 모델에 따라 인공 데이터 세트를 구성할 것이다. 우리의 작업은 우리의 데이터 세트에 포함된 유한한 예제를 사용하여 이 모델의 매개 변수를 복구하는 것이다. 우리는 데이터를 쉽게 시각화할 수 있도록 저차원적으로 유지할 것이다. 다음 코드에서, 우리는 각각 표준 정규 분포에서 샘플링된 2개의 특징으로 구성된 1000개의 예를 포함하는 데이터 세트를 생성한다. 따라서 우리의 합성 데이터 세트는 $\mathbf{X}\in \mathbb{R}^{1000 \times2}$ 매트릭스가 될 것이다.

데이터 세트를 생성하는 진정한 매개 변수는 다음과 같다. $\mathbf{w} = [2, -3.4]^\top$ 및 $b = 4.2$, 그리고 우리의 합성 라벨은 잡음 항이 $\epsilon$인 다음 선형 모델에 대해 다음과 같이 할당될 것이다.

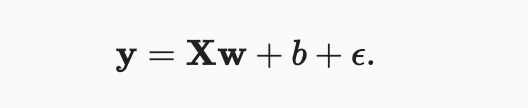
$\epsilon$는 features 및 labels에서 잠재적인 측정 오류를 캡처하는 것으로 생각할 수 있다. 우리는 표준 가정이 유지되고 따라서 $\epsilon$가 평균이 0인 정규 분포를 따른다고 가정할 것이다. 문제를 쉽게 하기 위해, 우리는 그것의 표준 편차를 0.01로 설정할 것이다. 다음 코드는 우리의 합성 데이터 세트를 생성한다.

def synthetic_data(w, b, num_examples):  #@save
    """Generate y = Xw + b + noise."""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

features의 각 행은 2차원 데이터 예제로 구성되며 labels의 각 행은 1차원 레이블 값 (스칼라) 으로 구성된다.

print('features:', features[0],'\nlabel:', labels[0])

# Output
features: tensor([-1.4598, -0.7918])
label: tensor([3.9780])

두 번째 특징 features[:, 1] 및 labels를 사용하여 산점도를 생성하면 둘 사이의 선형 상관 관계를 명확하게 관찰 할 수 있다.

d2l.set_figsize()
# The semicolon is for displaying the plot only
d2l.plt.scatter(features[:, (1)].detach().numpy(), labels.detach().numpy(), 1);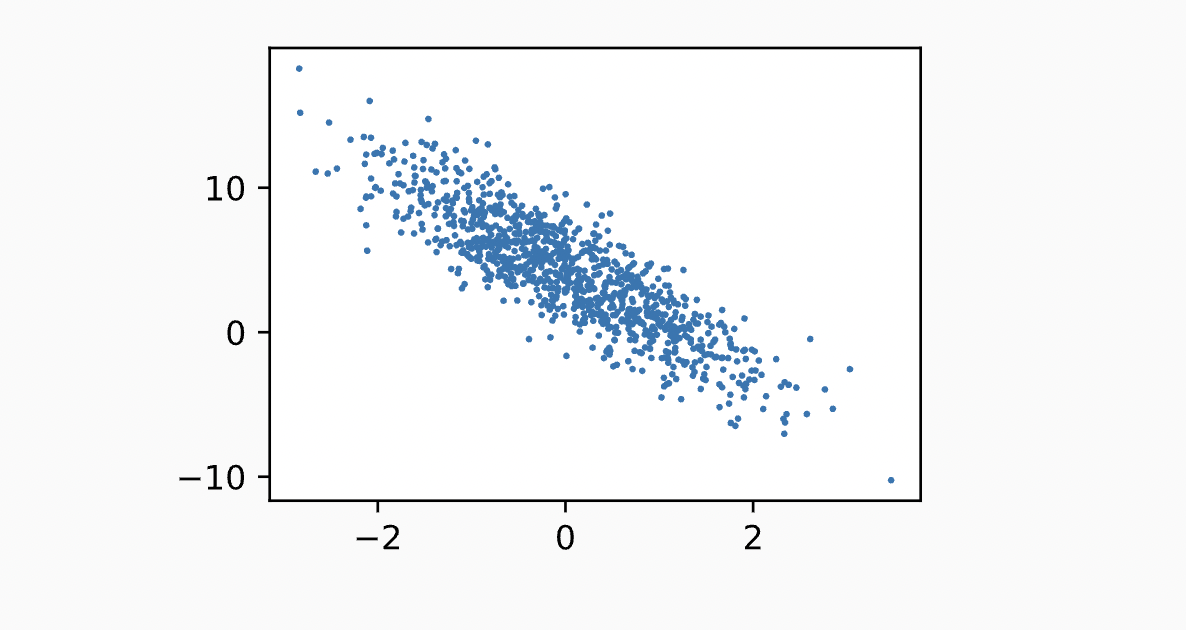

3.2.2. Reading the Dataset

학습 모델은 데이터 세트를 여러 번 통과하고 한 번에 하나의 미니 배치를 가져 와서 모델을 업데이트하는 데 사용하는 것으로 구성된다.이 과정은 기계 학습 알고리즘을 훈련시키는 데 매우 중요하므로 데이터 세트를 섞고 미니 배치로 액세스하는 유틸리티 함수를 정의하는 것이 좋다.

코드에서는 data_iter 함수 를 정의하여 이 기능의 구현 가능한 한 가지를 보여준다. 함수 (배치 크기, 특징 행렬, 레이블 벡터를 취하여 크기가 batch_size.)는 미니배치를 산출해 각 미니배치는 특징과 레이블의 튜플로 구성된다.

def data_iter(batch_size, features, labels):
	num_examles = len(features)
    indices = list(range(num_examples))
    # The examples are read at random, in no particular order
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
    	batch_indices = torch.tensor(
        	indices[i : min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

일반적으로 우리는 연산을 병렬화하는 데 탁월한 GPU 하드웨어를 활용하기 위해 적당한 크기의 미니 배치를 사용하고 싶다.각 예제는 모델을 통해 병렬로 공급할 수 있고 각 예제에 대한 손실 함수의 기울기도 병렬로 취할 수 있기 때문에 GPU를 사용하면 단일 예제를 처리하는 데 걸리는 시간보다 훨씬 더 많은 시간 내에 수백 개의 예제를 처리 할 수 있다.

직관적으로 보기 위해 데이터 예제의 첫 번째 작은 배치를 읽고 인쇄해 보겠다. 각 미니배치의 피처 모양은 미니배치 크기와 입력 피처 수를 모두 알려준다.마찬가지로 라벨의 미니 배치는 batch_size에 의해 주어진 모양을 갖는다.

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
	print(X, '\n', y)
    break

# Output
tensor([[-1.0999,  0.4855],
        [ 1.9538,  1.0919],
        [ 1.5107, -0.2886],
        [ 0.9734, -0.2309],
        [ 0.6716, -1.0258],
        [-0.9730, -0.7290],
        [-0.6671, -0.8925],
        [-0.7708, -0.3410],
        [ 0.0294, -1.2729],
        [-0.7009,  0.5991]])
 tensor([[0.3487],
        [4.4049],
        [8.1914],
        [6.9287],
        [9.0329],
        [4.7465],
        [5.9153],
        [3.8213],
        [8.5887],
        [0.7470]])

반복을 실행할 때 전체 데이터셋이 모두 소진될 때까지 고유한 미니배치를 연속적으로 얻는다. 위에서 구현한 반복은 학습 목적으로는 좋지만 실제 문제에서는 어려움을 겪을 수 있어 비효율적이다. 예를 들어 메모리에 모든 데이터를 로드하고 많은 랜덤 메모리 액세스를 수행해야 한다. 딥러닝 프레임워크에 구현된 내장 반복기는 훨씬 더 효율적이며 파일에 저장된 데이터와 데이터 스트림을 통해 공급되는 데이터를 모두 처리할 수 있다.

3.2.3. Initializing Model Parameters

minibatch stochastic gradient descent를 통해 모델의 매개 변수를 최적화하기 전에 먼저 몇 가지 매개 변수를 준비해야 한다. 다음 코드에서는 평균이 0이고 표준 편차가 0.01인 정규 분포에서 난수를 샘플링하고 편향을 0으로 설정하여 가중치를 초기화한다.

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

매개 변수를 초기화한 후 다음 작업은 데이터가 충분히 잘 맞을 때까지 매개 변수를 업데이트하는 것이다.업데이트 할 때마다 매개 변수와 관련하여 손실 함수의 기울기를 취해야한다.이 기울기가 주어지면 손실을 줄일 수 있는 방향으로 각 파라미터를 업데이트할 수 있다.

아무도 그라디언트를 명시적으로 계산하기를 원하지 않기 때문에 (지루하고 오류가 발생하기 쉬움) Section 2.5에 소개된 자동 미분을 사용하여 그래디언트를 계산한다.

3.2.4. Defining the Model

다음으로, 입력과 파라미터를 출력에 연결하여 모델을 정의해야 햔다. 선형 모델의 출력을 계산하려면 입력 피처 $\mathbf{X}$와 모델 가중치 $\mathbf{w}$의 행렬-벡터 내적을 가져와 각 예제에 오프셋 $b$을 추가하기만 하면 됩니다.$\mathbf{Xw}$ 아래는 벡터이고 $b$은 스칼라입니다.Section 2.1.3에 설명된 대로 브로드캐스팅 메커니즘을 호출한다.벡터와 스칼라를 추가하면 벡터의 각 구성 요소에 스칼라가 추가된다.

def linreg(X, w, b):  #@save
    """The linear regression model."""
    return torch.matmul(X, w) + b

3.2.5. Defining the Loss Function

모델을 업데이트하려면 손실 함수의 기울기를 취해야 하므로 먼저 손실 함수를 정의해야 한다. 여기서는 섹션 3.1에 설명된 대로 손실 제곱 함수를 사용한다. 구현 시, 우리는 참 값 y를 예측 값의 모양 y_hat으로 변환해야 합니다. 다음 함수에 의해 반환되는 결과도 y_hat과 같은 모양이 된다.

def squared_loss(y_hat, y):  #@save
    """Squared loss."""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

3.2.6. Defining the Optimization Algorithm

Section 3.1에서 논의한 것처럼 선형 회귀에는 closed-form solution이 있다. 그러나 이 책은 선형 회귀에 관한 책이 아니라 딥 러닝에 관한 책이다. 이 책에서 소개하는 다른 모델은 분석적으로 해결할 수 없으므로 이번 기회에 미니 배치 확률 적 경사 하강의 첫 번째 작업 예를 소개한다.

각 단계에서 데이터 세트에서 무작위로 추출한 하나의 미니 배치를 사용하여 매개 변수에 대한 손실의 기울기를 추정한다. 다음으로 손실을 줄일 수 있는 방향으로 매개변수를 업데이트한다. 다음 코드에서는 파라미터 집합, 학습률 및 배치 크기가 지정된 경우 미니배치 확률적 경사하강법 업데이트를 적용한다. 업데이트 단계의 크기는 학습 속도 lr에 의해 결정된다. 손실은 예제의 미니 배치에 대한 합계로 계산되므로, 일반적인 스텝 크기의 크기가 배치 크기 선택에 크게 좌우되지 않도록 단계 크기를 배치 크기 (batch_size) 로 정규화한다.

def sgd(params, lr, batch_size):  #@save
    """Minibatch stochastic gradient descent."""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

3.2.7. Training

이제 모든 부분이 준비되었으므로 기본 훈련 루프를 구현할 준비가 되었다. 딥 러닝 경력 전반에 걸쳐 거의 동일한 훈련 루프를 반복해서 볼 수 있으므로 이 코드를 이해하는 것이 중요하다.

각 반복에서 훈련 예제의 미니 배치를 가져와 모델에 전달하여 일련의 예측을 얻는다. 손실을 계산 한 후 각 매개 변수에 대한 기울기를 저장하여 네트워크를 통과하는 역방향 통과를 시작한다.마지막으로 최적화 알고리즘 sgd를 호출하여 모델 파라미터를 업데이트합니다.

요약하면 다음 루프를 실행합니다.

• 매개 변수를 초기화합니다. $(\mathbf{w}, b)$
• 완료될 때까지 반복
  - 컴퓨트 그래디언트 $\mathbf{g} \leftarrow \partial_{(\mathbf{w},b)} \frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} l(\mathbf{x}^{(i)}, y^{(i)}, \mathbf{w}, b)$
  - 업데이트 매개 변수 $(\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \eta \mathbf{g}$
  각 epoch에서 훈련 데이터 세트의 모든 예제를 통과하면 전체 데이터 세트 (data_iter 함수 사용) 를 반복한다(예제 수를 배치 크기로 나눌 수 있다고 가정). epochs의 수 num_epochs과 학습률 lr은 모두 하이퍼파라미터이며, 여기서는 각각 3과 0.03으로 설정한다.안타깝게도 하이퍼파라미터 설정은 까다롭고 시행착오를 통해 조정이 필요하다. 현재로서는 이러한 세부 사항을 생략하지만 나중에 Section 11에서 보충한다.

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # Minibatch loss in `X` and `y`
        # Compute gradient on `l` with respect to [`w`, `b`]
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # Update parameters using their gradient
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
  
# Output
epoch 1, loss 0.035526
epoch 2, loss 0.000131
epoch 3, loss 0.000050

이 경우, 우리가 직접 데이터 세트를 합성했기 때문에, 우리는 실제 매개 변수가 무엇인지 정확하게 알고 있다. 따라서, 우리는 훈련 루프를 통해 배운 것과 실제 매개 변수를 비교하여 훈련의 성공을 평가할 수 있다. 실제로 그들은 서로 매우 가까운 것으로 밝혀졌다.

print(f'error in estimating w: {true_w - w.reshape(true_w.shape)}')
print(f'error in estimating b: {true_b - b}')
  
# Output
error in estimating w: tensor([1.6928e-05, 1.8287e-04], grad_fn=<SubBackward0>)
error in estimating b: tensor([0.0004], grad_fn=<RsubBackward1>)

매개 변수를 완벽하게 복구 할 수 있다는 것을 당연하게 생각해서는 안된다. 그러나 기계 학습에서는 일반적으로 실제 기본 매개 변수를 복구하는 데 관심이 적고 매우 정확한 예측으로 이어지는 매개 변수에 더 관심이 있다. 다행스럽게도 어려운 최적화 문제에서도 확률적 경사 하강법은 심층 네트워크의 경우 매우 정확한 예측으로 이어지는 많은 파라미터 구성이 존재하기 때문에 매우 좋은 해를 찾을 수 있다.

3.2.8. Summary

• We saw how a deep network can be implemented and optimized from scratch, using just tensors and auto differentiation, without any need for defining layers or fancy optimizers.
• This section only scratches the surface of what is possible. In the following sections, we will describe additional models based on the concepts that we have just introduced and learn how to implement them more concisely.

3.2.9. Exercises

1. What would happen if we were to initialize the weights to zero. Would the algorithm still work?

2. Assume that you are Georg Simon Ohm trying to come up with a model between voltage and current. Can you use auto differentiation to learn the parameters of your model?

3. Can you use Planck’s Law to determine the temperature of an object using spectral energy density?

4. What are the problems you might encounter if you wanted to compute the second derivatives? How would you fix them?

5. Why is the reshape function needed in the squared_loss function?

6. Experiment using different learning rates to find out how fast the loss function value drops.

7. If the number of examples cannot be divided by the batch size, what happens to the data_iter function’s behavior?