3.1. Linear Regression

강의 : https://d2l.ai/chapter_linear-networks/linear-regression.html

3.1. Linear Regression

회귀 분석은 하나 이상의 독립 변수와 종속 변수 사이의 관계를 modeling하는 방법 집합을 말한다. 자연과학과 사회과학에서 회귀의 목적은 입력과 출력 사이의 관계를 characterize(특징짓는)하는 데 있다. 반면에 기계 학습은 예측과 가장 관련이 있다.

회귀 분석 문제는 수치 값을 예상하고 싶을 때마다 항상 사용된다. 흔한 예로는 (집이나 주식의) 가격 예측, (병원에서의)환자가 입원 기간 예측, (소매 판매에 대한)수요 예측 등 수없이 많다. 모든 예측 문제가 고전적인 회귀 문제인 것은 아니다. 후속 섹션에서는 분류 문제를 소개할 것이며, 여기서 일련의 범주 간의 구성원의 자격을 예측하는 것이 목표이다.

3.1.1. Basic Elements of Linear Regression

Linear regression 은 회귀에서 가장 단순하고 유명한 일반적인 툴일 것이다. 19세기로 거스러 올라가보면, 선형회귀는 는 몇 가지 간단한 가정으로부터 나온다. 첫째, 우리는 독립 변수 x와 종속 변수 y 사이의 관계가 선형이라고 가정한다. 즉, 관측치에 대한 약간의 noise가 주어졌을 때 y는 x에 있는 요소의 가중 합으로 표현될 수 있다. 둘째, 우리는 모든 noise가 잘 동작한다고 가정한다(following a Gaussian distribution).

machine learning 용어에서, 데이터 세트를 training dataset or training set 라고 하며, 각 행을 example (또는 data point, data instance, sample )라고 한다. 우리가 예측하려는 것은 label (또는 target)이라고 불립니다. 예측의 기반이 되는 독립 변수를 features (또는 covariates )이라고 한다.

일반적으로 $n$을 사용하여 데이터 세트의 예제 수를 표시한다. 우리는 데이터 예제를 $i$로 색인화하여 각 입력을 $x^{(i)}=[x_1^{(i)}, x_2^{(i)}]^T$로 표시하고 해당 레이블을 $y^{(i)}$로 표시한다.

3.1.1.1. Linear Model

linearity assumption에서는 target(price)이 features(area and age)의 가중합으로 표현될 수 있다.

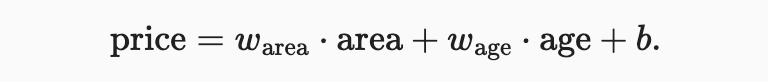
여기서 $w_area$, $w_age$는 weights 이고, b는 bias(also called an offset or intercept). 라고 부른다. 가중치는 각 feature가 우리의 예측에 미치는 영향을 결정하며, bias는 모든 feature가 0을 취할 때 예측 가격이 어떤 값을 가져야 하는지를 말해준다. 비록 우리가 면적이 0인 집이나 정확히 0년 된 집을 보지 못해도, 우리는 여전히 bias가 필요하다. 아니면, 우리는 모델의 표현력을 제한할 것이다. 엄밀히 말하면, 위는 입력 feature의 affine transformation으로, 추가된 bias을 통해 translation이 결합된 가중 합계를 통한 features의 linear transformation이 특징이다.

데이터셋이 주어지면, 우리의 목표는 평균적으로 우리의 모델에 따라 만들어진 예측이 데이터에서 관찰된 실제 가격에 가장 잘 맞도록 weghts w와 bias $b$를 선택하는 것이다. 입력 기능의 affine transformation에 의해 출력 예측이 결정되는 모델은 linear models이며, 여기서 아핀 변환은 선택된 가중치와 편향으로 지정된다.

기계 학습에서 우리는 보통 고차원 데이터 세트로 작업하기 때문에 선형 대수 표기법을 사용하는 것이 더 편리하다. 우리의 입력값이 $d$ features로 구성됐을 때, 예측 $y_hat$ (in general the “hat” symbol denotes estimates) 는 다음과 같이 표현한다.


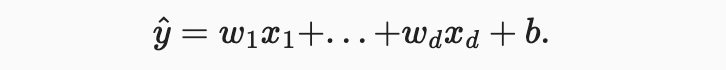
주어진 x로 $y$를 예측하기 위한 최선의 모델이 선형이라고 믿는다고 해도, 모든 $1 \leq i \leq n$에 대해 $\mathbf{w}^\top \mathbf{x}^{(i)}+b$ 와 똑같은 $n$개 예제의 실제 데이터 세트를 찾는 걸 기대하지는 않을 것이다. 예를 들어, features X와 labels y를 관측하기 위해 사용하는 도구는 모두 소량의 측정 오차가 발생할 수 있다. 따라서 기본 관계가 선형이라고 확신하는 경우에도 이러한 오류를 설명하기 위해 noise term을 통합한다.

최적의 매개 변수(또는 모델 매개 변수) w와 $b$를 검색하기 전에, (i) 주어진 모델에 대한 품질 측정과 (ii) 품질을 개선하기 위한 모델을 업데이트하는 절차, 두 가지가 더 필요할 것이다.

3.1.1.2. Loss Function

어떻게 데이터를 우리 모델에 fit할지 생각해보기 전에, fitness의 정도를 정해야 한다. loss function 은 타겟의 real 과 predicted 값 사이의 거리를 정량화 한다. 손실은 일반적으로 음수가 아니며 작은 값일수록 더 좋고 완벽한 예측은 0의 손실이 발생한다. 회귀 문제에서 가장 일반적인 손실 함수는 squared error(오차 제곱)이다. 예제 $i$에 대한 우리의 예측이 $\hat{y}^{(i)}$이고 해당 실제 레이블이 $y^{(i)}$일 때 제곱 오차는 다음과 같이 주어진다.

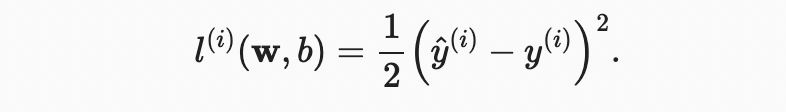
상수 $\frac{1}{2}$는 실제 차이를 만들지 않지만 손실의 도함수를 구할 때 없어지기 때문에 개념적이라는 것을 알수 있다. 훈련 데이터 세트가 제공되어 경험적 오류는 모델 매개 변수의 함수일 뿐이다. 더 정확하게 알아보기 위해, 아래에서 1차원 입력 문제에서 선형 회귀 모델의 적합성을 시각화한다.

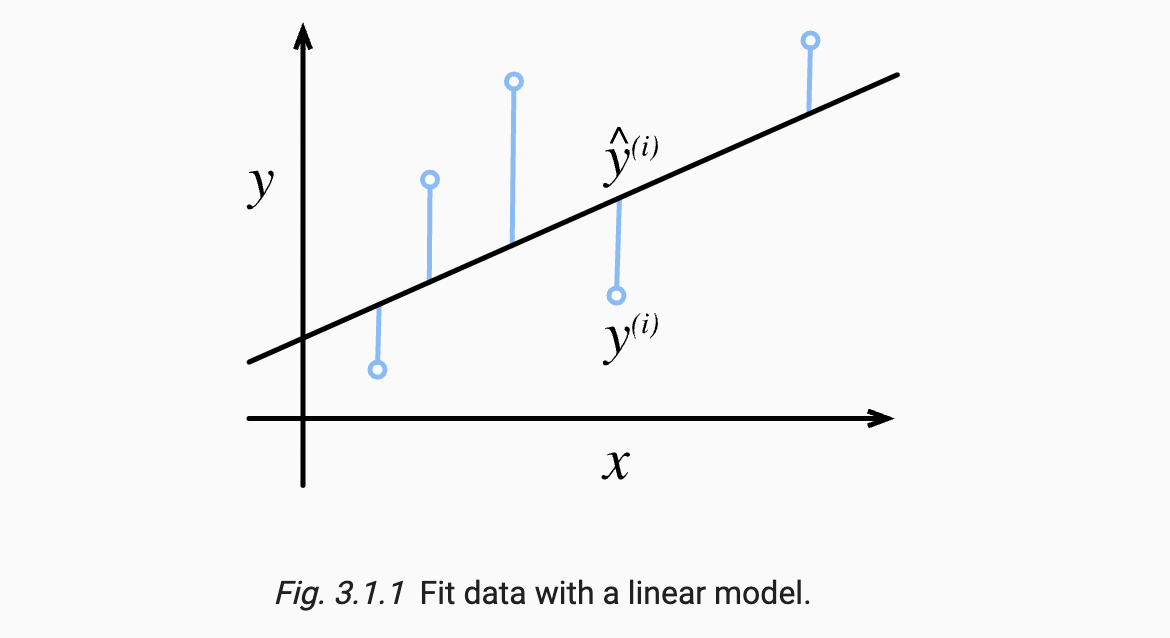
quadratic dependence로 인해 추정치 $\hat{y}^{(i)}$와 대상 $y^{(i)}$ 사이의 큰 차이는 손실이 더 큰 값으로 이어진다. $n$개 예제의 전체 데이터 세트에서 모델의 품질을 측정하기 위해, 우리는 단순히 훈련 세트의 손실을 평균(또는 동등하게 합계)낸다.

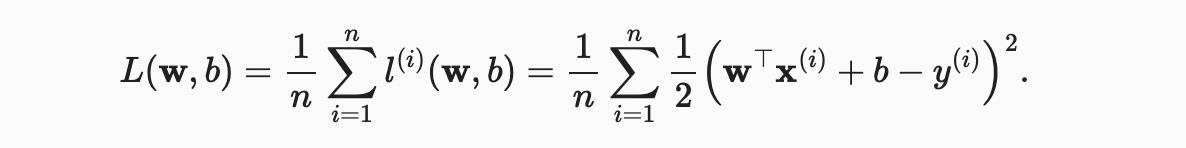
모델을 훈련할 때, 우리는 모든 훈련 예제에 걸쳐 총 손실을 최소화하는 매개 변수($\mathbf{w}^*,$ $b^*$)를 찾고 싶다.

3.1.1.3. Analytic Solution

선형 회귀는 이례적으로 단순한 최적화 문제이다. 이 책에서 만날 다른 모델들과는 달리, linear regression은 단순한 공식을 적용함으로써 분석적으로 해결된다. 먼저, 모두 1로 구성되계 설계된 행렬에 열을 추가하여 bias $b$를 매개 변수 $\mathbf{w}$로 가정할 수 있다. 그러면 우리의 예측 문제는 $||\mathbf{y} - \mathbf{X}\mathbf{w}||^2$로 최소화 된다. 손실 표면에는 임계점이 하나만 있으며 이는 전체 도메인에 걸친 손실의 최소값에 해당합니다. $\mathbf{w}$에 대하여 손실의 미분을 얻고 이 값을 0으로 설정하면 다음과 같다.

선형 회귀 분석과 같은 단순한 문제가 분석적 해결책을 허용할 수도 있지만, 이러한 단순함에 익숙해지면 안 된다. analytic solution은 편리한 수학적 분석을 허용하지만 analytic solution의 요구 사항은 너무 제한적이어서 딥 러닝을 모두 제외할 수 있다.

3.1.1.4. Minibatch Stochastic Gradient Descent

모델을 분석적으로 해결할 수 없는 경우에도, 실제로 모델을 효과적으로 훈련시킬 수 있다. 게다가, 많은 작업에서, 최적화하기 어려운 모델들이 훨씬 더 나은 것으로 증명되고, 그것들을 훈련시키는 방법을 알아내는 것은 결국 수고를 들일 만한 가치가 있다.

거의 모든 딥러닝 모델을 최적화 시키는 중요 기술은, 손실 함수를 점진적으로 낮추는 방향으로 매개 변수를 업데이트하여 오류를 반복적으로 줄이는 것으로 구성된다. 이 알고리즘을 gradient descent (경사 하강)이라고 한다.

가장 기본적인 경사하강법의 적용은 손실함수의 도함수를 적용하는 것인데, 데이터셋의 모든 단일 example에 대해 계산된 손실의 함수이다. 실제 적용에서, 이것은 아주 느릴 수 있다: 하나의 업데이트 발생 전에 모든 데이터셋을 넘겨줘야 한다. 따라서, 종종 업데이트를 계산해야 할 때마다 임의의 미니 배치 예시를 샘플링하는 것으로 만족하는데, minibatch stochastic gradient descent 라고 불리는 변형이다.

각 반복에서, 먼저 고정된 훈련 예제로 구성된 미니배치 $\mathcal{B}$ 를 무작위로 샘플링한다. 그런 다음 모델 매개 변수와 관련하여 미니 배치의 평균 손실의 도함수(기울기)를 계산한다. 마지막으로, 우리는 기울기에 미리 결정된 양의 값 $\eta$을 곱하고 현재 매개 변수 값에서 결과 항을 뺀다.

다음과 같이 업데이트를 수학적으로 표현할 수 있다. ($\partial$는 부분 도함수를 나타낸다)

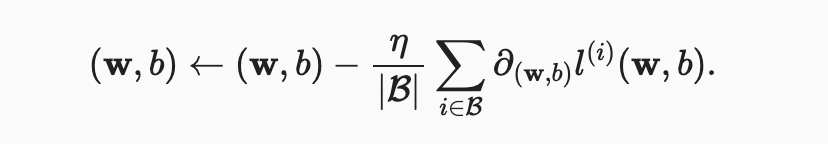
요약하자면, 알고리즘의 단계는 다음과 같다. (i) 일반적으로 무작위로 모델 매개 변수의 값을 초기화한다. (ii) 음의 기울기 방향으로 매개 변수를 업데이트하면서 데이터에서 무작위 미니배치를 반복적으로 샘플링한다. 2차 손실과 아핀 변환의 경우 다음과 같이 명시적으로 작성할 수 있다.

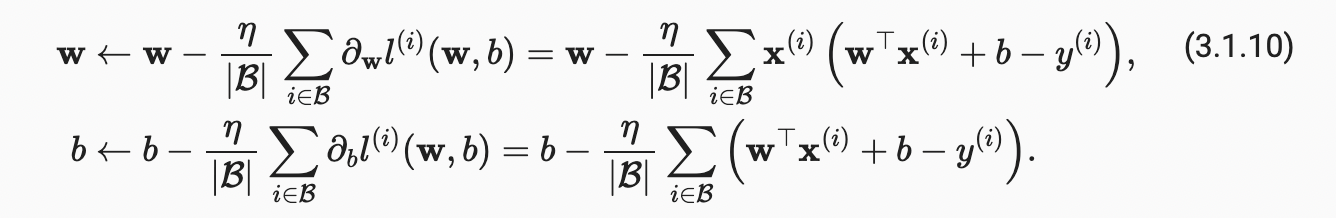
여기서, 보다 간단한 벡터 표기법은 계수의 관점에서 사물을 표현하는 것보다 수학을 훨씬 더 읽기 쉽게 만든다. 여기서 $|\mathcal{B}|$ 는 각 미니배치에서의 예제의 수를 보여주고 $\partial$는 learning rate 라고 한다. 배치 크기와 학습률 값은 수동으로 사전 지정되며 일반적으로 모델 훈련을 통해 학습되지 않는다는 것을 알아야 한다. 조정 가능하지만 훈련 loop 중에 업데이트 되지는 않는 이런 매개변수를 hyperparameters 라고 부른다. hyperparameters tuning 은 하이퍼파라미터가 선택되는 과정이며, 일반적으로 별도의 validation dataset(또는 validation set)에서 평가된 훈련 루프 결과에 따라 조정해야 한다.

사전 결정된 횟수로 반복 훈련 후(또는 다른 중지 기준이 충족될 때까지) $\hat{\mathbf{w}}, \hat{b}$로 표시된 추정 모델 매개 변수를 기록한다. 우리의 함수가 선형이고 노이즈가 없다고 해도, 이런 매개변수는 손실에 대해 정확한 최소화가 되지 않을 것이다. 왜냐하면 알고리즘이 최소화를 향해 천천히 수렴하지만 제한된 수의 단계에서 정확하게 이를 달성할 수는 없기 때문이다.

선형 회귀는 전체 도메인에 대해 최소값이 하나만 있는 학습 문제이다. 그러나 심층 네트워크와 같은 더 복잡한 모델의 경우 손실 표면에는 여러개의 최소값이 있다. 다행히도, 딥 러닝 실무자들은 훈련 세트의 손실을 최소화하는 매개 변수를 찾기 위해 거의 고군분투하지 않는다. 더 어려운 작업은 우리가 이전에 보지 못한 데이터에서 낮은 손실을 달성할 매개 변수, 즉 generalization (일반화)라는 것이다. 우리는 책 전반에 걸쳐 이 주제들로 돌아간다.

3.1.1.5. Making Predictions with the Learned Model

$\hat{\mathbf{w}}^\top \mathbf{x} + \hat{b}$ 모델이 주어졌을 때, 우리는 이제 면적 $x_1$과 연령 $x_2$가 주어졌을 때 새로운 집(훈련 데이터에 없던 것들)의 판매 가격을 예측할 수 있다. 주어진 특징을 대상으로 추정하는 것을 일반적으로 prediction 또는 inference 이라고 한다. 보통 통계학에서는 inference 딥러닝에서는 prediction이라고 부른다.

3.1.2. Vectorization for Speed

우리의 모델을 훈련할 때, 일반적으로 전체 미니 배치의 예제들를 동시에 처리하려고 한다. 이를 효율적으로 수행하려면 비용이 많이 드는 for-loops 를 파이썬으로 작성하는 것보다 계산을 벡터화하고 빠른 선형 대수 라이브러리를 활용해야 한다.

%matplotlib inline
import math
import time
import numpy as np
import torch
from d2l import torch as d2l

이것이 왜 그렇게 중요한지 설명하기 위해, 우리는 벡터를 추가하는 두 가지 방법을 고려할 수 있다. 먼저, 모든 것을 포함하는 두 개의 10000차원 벡터를 인스턴스화한다. 한 가지 방법에서 파이썬 for-loop으로 벡터를 루프할 것이다. 다른 방법에서는 +에 대한 단일 호출을 해볼 것이다.

n = 10000
a = torch.ones(n)
b = torch.ones(n)

이 책에서는 실행 시간을 자주 benchmark하기 때문에 타이머를 정의하겠다.

class Timer:  #@save
    """Record multiple running times."""
    def __init__(self):
        self.times = []
        self.start()

    def start(self):
        """Start the timer."""
        self.tik = time.time()

    def stop(self):
        """Stop the timer and record the time in a list."""
        self.times.append(time.time() - self.tik)
        return self.times[-1]

    def avg(self):
        """Return the average time."""
        return sum(self.times) / len(self.times)

    def sum(self):
        """Return the sum of time."""
        return sum(self.times)

    def cumsum(self):
        """Return the accumulated time."""
        return np.array(self.times).cumsum().tolist()

이제 workloads를 기준화 하겠다. 먼저, 한 번에 하나의 좌표를 for-loop을 사용하여 추가한다.

c = torch.zeros(n)
timer = Timer()
for i in range(n):
    c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'

# Output
'0.10353 sec'

또는, 우리는 요소별 합계를 계산하기 위해 다시 로드된 + 연산자를 사용한다.

timer.start()
d = a + b
f'{timer.stop():.5f} sec'

# Output
'0.00028 sec'

여러분은 아마 두 번째 방법이 첫 번째 방법보다 엄청나게 빠르다는 것을 알아차렸을 것이다. 벡터화된 코드는 종종 대규모로 속도를 높일 수 있다. 게다가, 우리는 더 많은 수학을 라이브러리에 적용하고 많은 계산이 필요없기 때문에 오류의 가능성을 줄인다.

3.1.3. The Normal Distribution and Squared Loss

선형 회귀는 1795년에 가우스에 의해 발명되었으며, 그는 또한 정규 분포(Gaussian라고도 함)를 발견했다. normal distribution(정규 분포)와 선형 회귀 분석은 더 깊은 연관이 있는 것으로 밝혀졌다. 기억을 상기 시키기 위해, 평균 $\mu$와 분산 $\mu^2$(표준 편차 $\mu$)를 갖는 정규 분포가 다음과 같이 주어지는 것을 생각하자.

아래에서는 정규 분포를 계산하는 파이썬 함수를 정의한다.

def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

이제 정규 분포를 시각화할 수 있다.

# Use numpy again for visualization
x = np.arange(-7, 7, 0.01)

# Mean and standard deviation pairs
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
         ylabel='p(x)', figsize=(4.5, 2.5),
         legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])

위에서 볼 수 있듯이, 평균은 $x$축을 따른 이동에 대응하여 변화하고, 분산을 증가시키면 분포가 분산되어 피크가 낮아진다. 평균 제곱 오차 손실 함수(또는 단순히 제곱 손실)를 사용하여 선형 회귀를 동기화하는 한 가지 방법은 관측치가 잡음이 많은 관측치로부터 발생한다고 공식적으로 가정하는 것이다. 여기서 노이즈는 일반적으로 다음과 같이 분포한다.

따라서, 우리는 이제 다음을 통해 주어진 $\mathbf{x}$에 대한 특정 $y$를 볼 수 있는 likelihood을 쓸 수 있다.

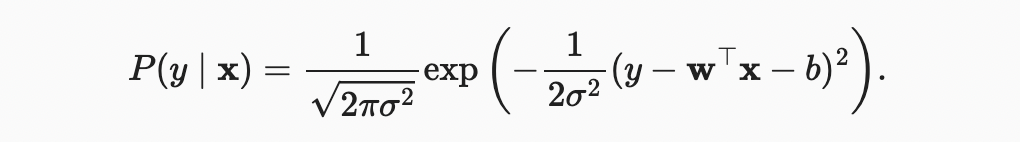
이제 maximum likelihood 원리에 따라 매개 변수 $\mathbf{w}$와 $b$의 최적 값은 전체 데이터 세트의 가능성을 최대화하는 값이다.

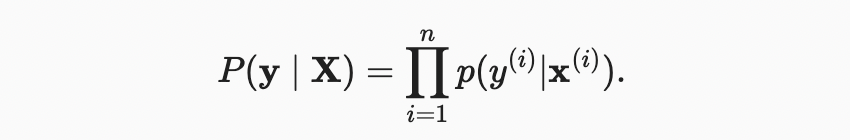
최대 가능 원리에 따라 선택한 추정기를 maximum likelihood estimators 라고 한다. 많은 지수함수의 곱을 최대화하는 것은 어려워 보일 수 있지만, 우리는 대신 likelihood의 로그를 최대화함으로써 목표를 변경하지 않고 일을 크게 단순화할 수 있다. 역사적 이유로, 최적화는 최대화보다는 최소화로 표현되는 경우가 더 많다. 따라서 아무것도 변경하지 않고 negative log-likelihood($-\log P(\mathbf y | \mathbf X)$)를 최소화할 수 있다. 다음과 같이 표현할 수 있다.

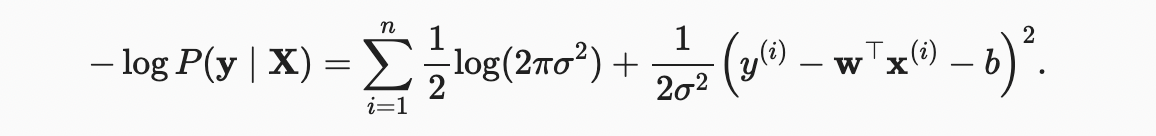
$\sigma$가 고정된 상수라고 가정하면, $\mathbf{w}$ 또는 $b$에 의존하지 않기 때문에 첫 번째 항을 무시할 수 있다. 두 번째 항은 multiplicative constant $\frac{1}{\sigma^2}$를 제외하고, 앞에서 소개한 오차 손실 제곱과 동일하다. 다행히도, 솔루션은 $\sigma$에도 의존하지 않는다. 따라서 평균 제곱 오차를 최소화하는 것은 가우스 노이즈를 가정할 때 선형 모델의 최대 우도 추정과 동일하다.

3.1.4. From Linear Regression to Deep Networks

지금까지 우리는 선형 모델에 대해서만 이야기했다. 신경망은 훨씬 더 풍부한 모델들을 커버하지만, 우리는 선형 모델을 신경망의 언어로 표현함으로써 신경 네트워크로 생각하기 시작할 수 있다. 우선, "레이어" 표기법으로 사물을 다시 쓰는 것으로 시작하자.

3.1.4.1. Neural Network Diagram

딥러닝 실무자들은 자신의 모델에서 일어나는 일을 시각화하기 위해 도표를 그리는 것을 좋아한다. 아래에서는, 우리의 선형 회귀 모델을 neural network로 묘사했다. 이러한 다이어그램은 각 입력이 출력에 연결되는 방식과 같은 연결 패턴을 강조하지만 weights나 biases에 의해 결정된 값은 보여주지 않는다.

위에서 보이는 신경망의 경우, 입력값은 $x_1, \ldots, x_d$이고, $d$를 입력 계층의 입력 수 또는 기능 차원이라고 한다. 출력은 $o_1$이며 출력 계층의 출력 수는 1입니다. 계산이 발생하는 위치에 초점을 두면서, 전통적으로 우리는 계층을 계산할 때 입력 계층을 고려하지 않는다. 즉, 위의 신경망에 대한 층수는 1이다. 우리는 선형 회귀 모델을 하나의 인공 뉴런으로 구성된 신경 네트워크 또는 단일 층 신경 네트워크로 생각할 수 있다.

선형 회귀의 경우, 모든 입력이 모든 출력에 연결되는(이 경우 출력은 하나) 이러한 변환을 fully-connected layer or dense layer 라고 말한다. 우리는 다음 장에서 이런 계층으로 구성된 네트워크에 대해 더 많이 이야기할 것이다.

3.1.4.2. Biology

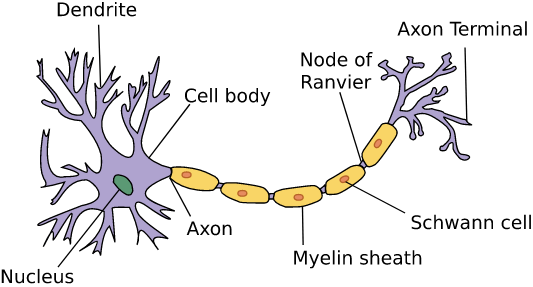
3.1.5. Summary

• Key ingredients in a machine learning model are training data, a loss function, an optimization algorithm, and quite obviously, the model itself.
• Vectorizing makes everything better (mostly math) and faster (mostly code).
• Minimizing an objective function and performing maximum likelihood estimation can mean the same thing.
• Linear regression models are neural networks, too.

3.1.6. Exercises

In loacal Jupyter Notebook @@