2.4. Calculus

강의: https://d2l.ai/chapter_preliminaries/calculus.html#exercises

2.4. Calculus

다각형의 면적을 찾는 것은 고대 그리스인들이 polygons(다각형)을 삼각형으로 나누고 그들의 면적을 합한 2,500년 전까지 신비롭게 남아 있었다. 원과 같은 구부러진 모양의 면적을 찾기 위해 고대 그리스인들은 다각형을 이런 모양으로 새겼다. 아래에서 보는 바와 같이, 동일한 길이의 변이 더 많은 내접 다각형은 원에 더 잘 접근한다. 이 과정은 method of exhaustion이라고도 알려져 있다.

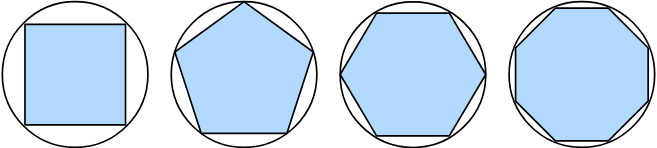
딥러닝에서, 우리는 모델을 훈련하고, 그들이 점점 더 많은 데이터를 볼수록 점점 더 좋아지도록 그들을 순차적으로 업데이트한다. 일반적으로, 더 좋아진다는 것은 "얼마나 우리의 모델이 구린지"를 알려주는 loss function 의 값을 최소화하는 것이다. 이 질문은 보기보다 더 예민하다. 궁극적으로, 우리가 정말 원하는 것은 한번도 보지 못한 데이터에서 잘 수행되는 모델을 만드는 것이다. 따라서 모델 장착 작업을 두 가지 주요 관점으로 나눌 수 있다: (i) optimization(최적화) - the process of fitting our models to observed data (ii) generalization(일반화) - the mathematical principles and practitioners’ wisdom that guide as to how to produce models whose validity extends beyond the exact set of data examples used to train them.

2.4.1. Derivatives and Differentiation

딥러닝에서 우리는 일반적으로 모델의 매개 변수와 관련하여 미분 가능한 loss functions을 선택한다. 간단히 말해 이는 각 매개변수에 대해, 그 매개변수를 극소의 작은 양으로 증가시키거나 감소시킬 때 손실이 얼마나 빨리 증가하거나 감소하는지 결정할 수 있다는 것을 의미한다.

입력 값과 출력 값이 둘다 scalar인 $f : ℝ → ℝ$ 함수가 있다고 하자. $f$의 limit가 존재한다면 derivative는 다음과 같다.

$f'(a)$가 존재하면, $f$는 $a$에 대해 differentiable(미분 가능)라고 할수 있다. 만약 f가 모든 구간마다 미분가능하다면, 이 함수는 이 구간에서 미분가능하다. $f'(a)$를 $x$에 대해서 $f(x)$의 순간변화율이라고 할 수 있다. 순간 변화율이라 불리는 것은 0에 가까운 $x$의 변화에 기초한다.

예를 들어 $u = f(x) = 3x^2-4x$ 를 정의한다.

%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l


def f(x):
    return 3 * x ** 2 - 4 * x

$x$를 1로 $h$가 0으로 향하게 설정한 후, $f(x+h)-f(x)\over h$ 의 결과는 2로 향한다. 비록 이 실험이 수학적 증명은 아니지만, 나중에 $x=1$일 때 $u'$는 2라는 것을 볼 것이다.

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

h = 0.1
for i in range(5):
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
    h *= 0.1
    
# Output
h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003

derivatives에 대한 몇 가지 같은 표기법을 알아보자. $y=f(x)$가 주어졌을 때

여기서 기호 $d\over dx$ 와 $D$는 미분 연산을 나타내는 미분 연산자이다. 다음 규칙을 사용하여 공통 기능을 구별할 수 있다.

위의 기본 함수들과 같은 몇 가지 단순한 함수들로부터 형성된 함수를 구별하기 위해, 다음의 규칙들이 우리에게 유용할 수 있다. 함수 $f$와 $g$ 모두 미분 가능하고 $C$가 정수라면, constant multiple rule 를 가질 수 있다.

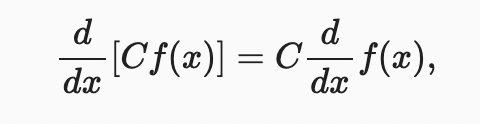
the sum rule

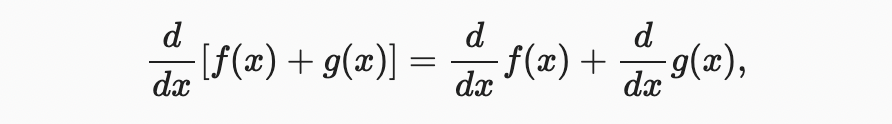
the product rule

the qoutient rule

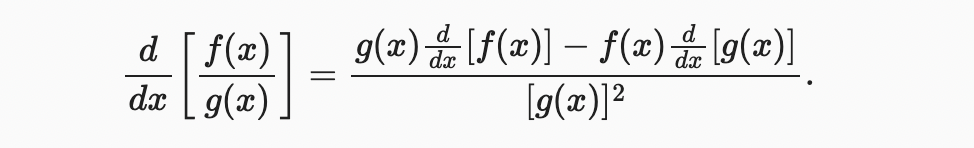
이제 위의 몇 가지 규칙을 적용하여
$u' = f'(x) = 6x -4$. 그래서 $x=1$로 설정하면 $u' = 2$가 된다. 이 도함수는 $u=f(x)$의 $x = 1$일때 곡선에 대한 접선의 기울기이기도 하다.

이 미분값의 해석을 시각화하기 위해, 우리는 파이썬의 유명한 plotting 라이브러리인 matplotlib을 사용할 것이다. matplotlib에서 생성된 도형의 속성을 구성하려면 몇 가지 함수를 정의해야 한다. 다음에서 use_svg_display 함수는 더 선명한 이미지를 위해 svg 수치를 출력하는 matplotlib 패키지를 지정합니다. 주석 #@save는 다음 함수, 클래스 또는 표현이 나중에 재정의되지 않고 직접 호출될 수 있도록 d2l 패키지에 저장되는 특수 표시이다(예: d2l.use_svg_display()).

def use_svg_display():  #@save
    """Use the svg format to display a plot in Jupyter."""
    backend_inline.set_matplotlib_formats('svg')

set_figsize 함수로 그림 크기를 지정한다. from matplotlib import pyplot as plt 라는 문구로 d2l 패키지에 저장되도록 표시되었기 때문에 d2l.plt를 직접 사용했습니다.

def set_figsize(figsize=(3.5, 2.5)):  #@save
    """Set the figure size for matplotlib."""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize

다음 set_axes 함수는 matplotlib에 의해 생성된 도형의 축의 속성을 설정한다.

#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """Set the axes for matplotlib."""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

figure configurations에 대한 이 세 가지 함수를 사용해, 우리는 책 전체에 걸쳐 많은 곡선을 시각화해야 하기 때문에 여러 곡선을 간결하게 plot하기 위한 plot 함수를 정의한다.

#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """Plot data points."""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # Return True if `X` (tensor or list) has 1 axis
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

이제 우리는 함수 $u=f(x)$와 $x=1$일때 $y=2x-3$의 접선을 그릴 수 있다.

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

2.4.2. Partial Derivatives

지금까지 우리는 단지 하나의 변수의 함수 미분화를 다루었다. 딥러닝에서 함수는 종종 많은 변수에 의존한다. 따라서, 우리는 미분 개념을 이러한 multivariate(다변수) 함수로 확장해야 한다.

$y=f(x_1, x_2,...,x_n)$ 함수가 $n$개의 변수와 있다. $i^{th}$ 매개변수 $x_i$에 대한 $y$의 partial derivative(부분 도함수)는 다음과 같다.

$∂y\over ∂x_i$ 계산을 위해, 간단히 $x_1,....,x_{i-1},x_{i+1},...,x_n$를 상수로 취하고 $x$에 대한 $y$의 도함수를 계산할 수 있다.

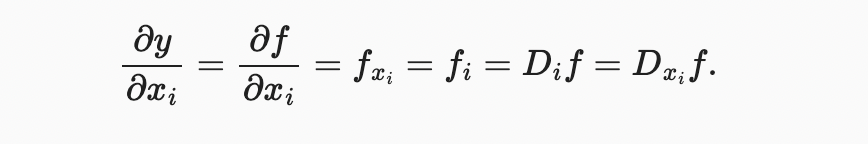
2.4.3. Gradients

우리는 다변량 함수의 모든 변수에 대한 부분 도함수를 연결하여 함수의 gradient 벡터를 얻을 수 있다. 함수 $f : ℝ → ℝ$의 입력값이 $n$차원 벡터 $x = [x_1,x_2,...,x_n]^T$이고 출력값은 스칼라이다. $x$에 대한 함수 $f(x)$의 기울기는 $n$개의 부분 미분 벡터이다.

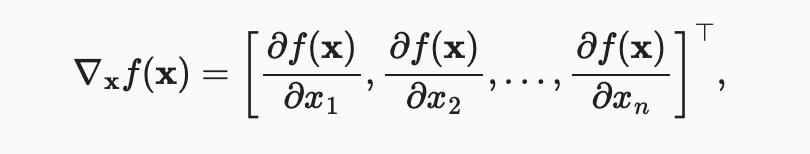
$x$를 $n$차원 벡터라고 가정하면, 다변량 함수를 미분할 때 다음과 같은 규칙이 자주 사용된다.

나중에 보겠지만, 딥러닝에서 gradients(기울기)는 최적화 알고리즘을 디자인하는데 유용하다.

2.4.4. Chain Rule

그러나 이러한 gradients는 찾기 어려울 수 있다. 딥러닝의 다변량 함수는 복합적이기 때문에 이러한 함수를 구별하기 위해 앞에서 언급한 어떤 규칙도 적용하지 못할 수 있기 때문이다. 다행히도, chain rule 을 통해 composite functions을 구별할 수 있다.

변수가 하나인 함수를 먼저 생각해보자. 함수 $y=f(u)$와 u=g(x)는 모두 미분가능며, chain rule은 다음과 같다. 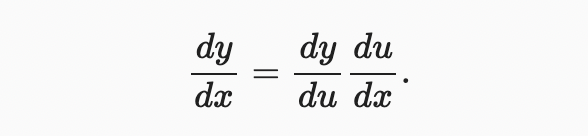 이제 함수가 임의의 변수를 갖는 일반적인 상황으로 눈을 돌려보자. 미분가능한 함수 $y가 변수 $u_1, u_2,..., u_m$을 갖고, 미분 가능한 함수 $u_i$는 변수 $x_1, x_2,..., x_n$을 가진다고 하자. chain rule은 다음과 같다.

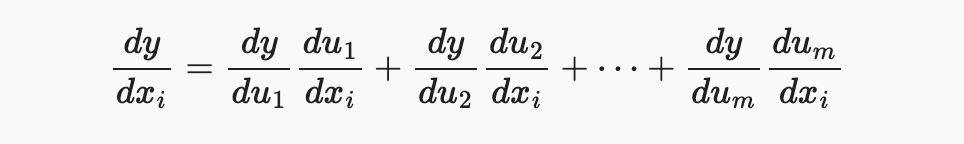
2.4.5. Summary

• Differential calculus and integral calculus are two branches of calculus, where the former can be applied to the ubiquitous optimization problems in deep learning.
• A derivative can be interpreted as the instantaneous rate of change of a function with respect to its variable. It is also the slope of the tangent line to the curve of the function.
• A gradient is a vector whose components are the partial derivatives of a multivariate function with respect to all its variables.
• The chain rule enables us to differentiate composite functions.

2.4.6. Exercises