2.3. Linear Algebra

강의 : https://d2l.ai/chapter_preliminaries/linear-algebra.html

2.3. Linear Algebra

이제 데이터를 저장하고 조작할 수 있으므로 이 책에서 다루는 대부분의 모델을 이해하고 구현하는 데 필요한 기본 linear algebra(선형 대수)의 하위 집합을 간략히 보겠다. 아래에서는 선형 대수학의 기본 수학 객체, 산술 및 연산을 소개하고, 수학적 표기법과 그에 상응하는 구현을 코드로 표현한다.

2.3.1 Scalars

만약 한번도 선형대수나 기계학습을 공부해보지 않았다면, 그렇다면 너의 수학에 대한 과거의 경험은 아마도 한 번에 하나의 숫자에 대해 생각하는 것으로 구성되었을 것이다. 그리고 만약 여러분이 수표장의 균형을 맞추거나 심지어 식당에서 저녁식사를 위해 돈을 지불했다면 여러분은 이미 숫자 쌍을 더하고 곱하는 것과 같은 기본적인 것들을 하는 방법을 알고 있을 것이다. 예를 들어, Palo Alto의 온도는 화씨 58도입니다. 공식적으로, 우리는 단지 하나의 숫자 수량으로 구성된 값을 scalars 라고 부른다. 이 값을 섭씨로 변환하려면 $c = 5/9(f - 32)$ 수식에서 $f$를 52로 설정하고 계산하면 된다. 여깃에서 $5, 9, 32$는 scalars 값이다. $c$와 $f$를 variables 라고 하며 알 수 없는 스칼라 값을 나타냅니다.

이 책에서는 스칼라 변수가 일반적인 소문자(예:$x, y, z$ )로 표시되는 수학적 표기법을 적용한다. 우리는 모든 (continuous) real-valued 스칼라(실수)의 공간을 ℝ로 표시한다. 편의상, 우리는 정확한 공간이 무엇인지에 대한 엄밀한 정의를 내릴 것이지만, $x∈ℝ$라는 표현이 $x$가 real-valued 스칼라라고 말하는 형식적인 방법이라는 것을 알아둬라. 기호 $∈$는 "in"이라고 발은될 수 있고 집합에 포함된다는 것을 의미한다. 비슷하게, $x$와 $y$의 값이 0아니면 1만 될 수 있다는 것을 $x, y ∈ {0, 1}$ 이렇게 적을 수 있다.

스칼라는 하나의 원소를 가진 텐서로 표현된다. 다음 글에서는 두 개의 스칼라를 인스턴스화하고 덧셈, 곱셈, 나눗셈 및 지수화와 같은 몇 가지 친숙한 산술 연산을 수행한다.

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x * y, x / y, x**y

# Output
(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))

2.3.2. Vectors

vector는 단순하게 스칼라 값의 리스트라고 생각해도 된다. 벡터의 이 값들을 elements(entries 또는 components)라 부른다. 벡터가 데이터셋의 예시를 나타낼 때, 벡터의 값은 실제 의미를 갖는다. 예를 들어, 대출 불이행 위험을 예측하기 위해 모델을 학습하는 경우, 각 신청자를 소득, 고용 기간, 이전 채무 불이행 수 및 기타 요인에 해당하는 구성요소의 벡터와 연결할 수 있다. 만약 우리가 병원 환자들이 잠재적으로 직면할 수 있는 심장마비의 위험을 연구한다면, 우리는 구성 요소가 그들의 가장 최근의 활력징후, 콜레스테롤 수치, 하루에 운동하는 분 등을 포착하는 벡터로 각 환자를 대표할 수 있을 것이다. 수학 표기법에서, 우리는 보통 벡터를 굵은 글씨로 나타낼 것이다.(e.f., x , y, z)

우리는 1차원 텐서를 통해 벡터로 작업한다. 일반적으로 텐서는 컴퓨터의 메모리 제한에 따라 임의의 길이를 가질 수 있다.

x = torch.arange(4)
x

# Output
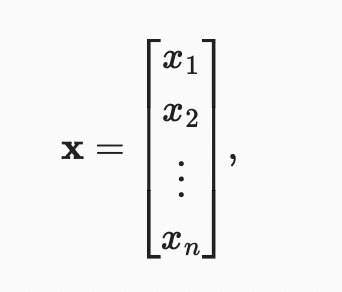
tensor([0, 1, 2, 3])

우리는 첨자를 사용하여 벡터의 모든 요소를 참조할 수 있다. 예를 들어, x의 $i^{th}$ 요소는 $x_i$로 참조할 수 있다. $x_i$ element는 스칼라이기 때문에 굵은 글씨를 쓰지 않는다. 대부분 열 벡터를 벡터의 기본 방향으로 간주한다. 수학에서 벡터x는 아래와 같이 적힌다.

$x_1, ..., x_n$은 벡터의 요소이다. 코드에서는 tesnor의 index로 접근한다.

x[3]

# Output
tensor(3)

2.3.2.1. Length, Dimensionality, and Shape

Section 2.1을 다시 봐보면, 벡터는 숫자들의 배열이다. 그래서 모든 배열이 길이가 있는듯이, 벡터로 그렇다. 수학 표기법에서, $n$ real-valued scalars로 구성된 vector x를 표현하고 싶으면, $**x**∈ ℝ^n$으로 표현한다. 벡터의 길이는 보통 dimension 이라고 불린다.

일반적인 파이썬 배열과 마찬가지로, 우리는 파이썬의 내장 len() 함수를 호출함으로써 텐서의 길이에 접근할 수 있다.

len(x)

# Output
4

텐서가 벡터를 나타낼 때(정확하게 하나의 축을 가지고), 우리는 또한 .shape 속성을 통해 벡터의 길이에 접근할 수 있다. 모양은 텐서의 각 축을 따라 길이(dimensionality)를 나열하는 튜플이다. 축이 하나만 있는 텐서의 경우 모양에는 요소가 하나만 있다.

x.shape

# Output
torch.Size([4])

이러한 맥락에서 "dimension"이라는 단어가 과부하되는 경향이 있고 사람들을 혼란스럽게 하는 경향이 있다는 것을 알아둬라. 명확히 하기 위해 vector 또는 axis의 dimensionality을 사용하여 길이, 즉 벡터 또는 축의 요소 수를 참조한다. 그러나 텐서의 dimensionality를 사용하여 텐서가 갖는 축의 수를 참조한다. 이런 의미에서 텐서의 어떤 축의 dimensionality는 그 축의 길이가 될 것이다.

2.3.3. Matrices

벡터가 순서 0에서 순서 1로 스칼라를 일반화하듯이, 행렬은 순서 1에서 순서 2로 벡터를 일반화한다. 일반적으로 굵은 글씨로 나타낼 행렬은(대문자로 e.g., X , Y, Z) 코드에서 두개의 축을 가진 텐서로 표현된다.

수학 표기법에서, 실수 스칼라값으로 $m$개의 행, $n$개의 열로 구성된 matrix A를 $A∈ ℝ^{m \times n}$로 표현한다. element $a_{ij}$ 는 $i^{th}$행 $j^{th}$열에 해당한다.

$A∈ ℝ^{m \times n}$ 인 A의 shape은 $(m, n)$ or $m \times n$이다. 특히, 행렬의 행과 열의 수가 같을 때, 그 모양은 정사각형이 되며, square matrix 이라고 한다.

두 개의 components $m$과 $n$을 가진 shape을 지정하여 $m \times n$ 행렬을 만들 수 있다.

A = torch.arange(20).reshape(5, 4)
A

# Output
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])

행($i$) 및 열($j$)에 대한 인덱스를 지정하여, 행렬 A의 $a_{ij}$스칼라 값에 접근하려면 $[A]_{ij}$로 표기한다. 주어지지 않은 행렬 A의 요소에 접근할 때, 행렬 A의 소문자를 색인 첨자$a_{ij}$와 함께 사용할 수 있다. 표기법을 단순하게 유지하기 위해 쉼표는 필요한 경우에만 ($a_{2,3j}$ and $[A]_{2i-1,3}$) 별도의 인덱스에 삽입된다.

축을 뒤집을수도 있다. 행과 열을 바꾼 행렬의 결과를 transpose 행렬이라고 한다. $A^T$로 표기하고 만약 $B = A^T$이면, $b_{ij} = a_{ji}$이다. A의 transpose 모양은 $n \times m$이다.

A.T

# Output
tensor([[ 0,  4,  8, 12, 16],
        [ 1,  5,  9, 13, 17],
        [ 2,  6, 10, 14, 18],
        [ 3,  7, 11, 15, 19]])

정사각행렬의 특별한 형태로서, symmetric matrix A은 그 transpose와 같다: $A = A^T$

 B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
 B
 
# Output
tensor([[1, 2, 3],
        [2, 0, 4],
        [3, 4, 5]])

B를 transpose와 비교

 B == B.T
 
# Output
tensor([[True, True, True],
        [True, True, True],
        [True, True, True]])

행렬은 유용한 데이터 구조이다. 행렬을 통해 다양한 모달리티의 데이터를 구성할 수 있습니다. 예를 들어, 행렬의 행은 서로 다른 집(데이터 예제)에 해당할 수 있지만 열은 다른 속성에 해당할 수 있습니다. 따라서 단일 벡터의 기본 방향은 열 벡터이지만, 표 형식의 데이터 집합을 나타내는 행렬에서는 각 데이터 예제를 행렬의 행 벡터로 처리하는 것이 더 일반적이다. 그리고, 뒷 장에서 볼 수 있듯이, 이것은 일반적인 딥러닝 예제를 가능하게 한다. 예를 들어 텐서의 가장 바깥쪽 축을 따라 데이터 예제의 미니 배치에 접근하거나 열거할 수 있으며, 미니 배치가 없는 경우 데이터 예제를 열거할 수 있다.

2.3.4. Tensors

벡터가 스칼라를 일반화하고 행렬이 벡터를 일반화하는 것처럼, 우리는 훨씬 더 많은 축을 가진 데이터 구조를 만들 수 있다. Tensors(이 하위 절의 "텐서"는 대수적 객체를 가리킴)는 임의의 수의 축을 가진 $n$차원 배열을 일반적인 방법으로 보여준다. 예를 들어, 벡터는 1차 텐서이고 행렬은 2차 텐서이다. 텐서는 $X, Y, Z$ 로 표기되며 색인 매커니즘은(e.g., $x_{ijk}$ and $[X]_{1,2i-1,3}$) 매트릭스와 비슷하다.

텐서는 높이, 너비, 색상 채널(빨강, 녹색, 파랑)에 해당하는 3축으로 n차원 배열로 생성되는 이미지로 작업을 시작할 때 더욱 중요해질 것이다. 우선 고차 텐서는 건너뛰고 기본에 집중한다.

X = torch.arange(24).reshape(2, 3, 4)
X
 
# Output
tensor([[[ 0,  1,  2,  3],
         [ 4,  5,  6,  7],
         [ 8,  9, 10, 11]],

        [[12, 13, 14, 15],
         [16, 17, 18, 19],
         [20, 21, 22, 23]]])

2.3.5. Basic Properties of Tensor Arithmetic

임의의 수의 축의 Scalars, vectors, matrices, 그리고 tensors (“tensors” in this subsection refer to algebraic objects) 유용한 특성 몇 가지를 가지고 있다. 예를 들어, 요소별 연산의 정의를 통해 요소별 단항 연산은 피연산자의 모양을 변경하지 않는다는 것을 알 수 있습니다. 비슷하게, 같은 모양의 어떤 두개의 텐서가 주어져도, 모든 이진 요소별 연산의 결과는 동일한 모양의 텐서가 될 것이다.

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()	# Assign a copy of 'A' to 'B' by allocation new memory
A, A + B
 
# Output
(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  2.,  4.,  6.],
         [ 8., 10., 12., 14.],
         [16., 18., 20., 22.],
         [24., 26., 28., 30.],
         [32., 34., 36., 38.]]))

특히, 두 행렬의 원소별 곱셈을 Hadamard product (수학 표기법 ⊙)이라고 한다. $i$ row $j$ column이 $b_{ij}$인 행렬 $B$$∈ℝ^{m\timesn}$을 생각해보자. 행렬 $A$와 $B$ 의 Hadamard product은 아래와 같다.

A * B
 
# Output
tensor([[  0.,   1.,   4.,   9.],
        [ 16.,  25.,  36.,  49.],
        [ 64.,  81., 100., 121.],
        [144., 169., 196., 225.],
        [256., 289., 324., 361.]])

텐서에 스칼라를 곱하거나 더해도 텐서의 모양은 변하지 않으며, 여기서 피연산자의 각 요소는 스칼라를 더하거나 곱한다.

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape
 
# Output
(tensor([[[ 2,  3,  4,  5],
          [ 6,  7,  8,  9],
          [10, 11, 12, 13]],

         [[14, 15, 16, 17],
          [18, 19, 20, 21],
          [22, 23, 24, 25]]]),
 torch.Size([2, 3, 4]))

2.3.6. Reduction

임의의 텐서로 수행할 수 있는 유용한 연산 중 하나는 요소의 합을 계산하는 것이다. Σ로 나타낸다. 길이가 $d$인 vector x의 요소들의 합은, $\displaystyle\sum_{i=1}^{d}{x_i}$로 표현할 수 있다. 코드에서는, 합계를 계산하기 위한 함수를 호출면 된다.

x = torch.arange(4, dtype=torch.float32)
x, x.sum()
 
# Output
(tensor([0., 1., 2., 3.]), tensor(6.))

우리는 임의의 모양 텐서 원소에 대한 합도 표현할 수 있다. $m\times n$ 행렬 $A$ 요소의 합은 $\displaystyle\sum_{i=1}^{m}$$\displaystyle\sum_{j=1}^{n}{a_{ij}}$ 로 표현할 수 있다.

A.shape, A.sum()
 
# Output
(torch.Size([5, 4]), tensor(190.))

기본적으로 합을 계산하기 위해 함수를 호출하면 모든 축을 따라 텐서가 스칼라로 줄어든다. 이때 텐서가 감소하는 축을 지정할 수 있다. 행렬을 예로 들어보자. 모든 행의 요소를 합산하여 행 차원(axis 0)을 줄이기 위해 함수를 호출할 때 axis=0을 지정한다. 입력 매트릭스는 출력 벡터를 생성하기 위해 축 0을 따라 감소하므로, 입력의 축 0의 치수는 출력 모양에서 손실된다.

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
 
# Output
(tensor([40., 45., 50., 55.]), torch.Size([4]))

axis=1로 지정하면 열의 요소들을 더함으로써 열 차원(axis 1)을 줄일 것이다. 따라서 입력 축 1의 치수는 출력 모양에서 손실된다.

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
 
# Output
(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))

행과 열을 둘다 합계를 통해 행렬을 줄이는 것은 행렬의 모든 요소를 합하는 것과 같다.

A.sum(axis=[0, 1])  # Same as `A.sum()`
 
# Output
tensor(190.)

또 다른 수식은 average 라고도 불리는 mean 이다. 합계를 원소의 총 개수로 나누어 평균을 계산한다. 코드에서는 임의의 형상의 텐서에 대한 평균을 계산하는 함수를 호출할 수 있다.

A.mean(), A.sum() / A.numel()
 
# Output
(tensor(9.5000), tensor(9.5000))

마찬가지로, 평균을 계산하는 함수도 지정된 축을 따라 텐서를 줄일 수 있습니다.

A.mean(axis=0), A.sum(axis=0) / A.shape(0)
 
# Output
(tensor([ 8.,  9., 10., 11.]), tensor([ 8.,  9., 10., 11.]))

2.3.6.1 Non-Reduction Sum

하지만, 합 또는 평균을 계산하는 함수를 호출할 때 축 수를 변경하지 않고 유지하는 것이 유용할때가 있다.

sum_A = A.sum(axis=1, keepdims=True)
sum_A

# Output
tensor([[ 6.],
        [22.],
        [38.],
        [54.],
        [70.]])

예를 들어, sum_A가 각 행을 더한 후에도 여전히 두개의 축을 가지고 있기 때문에, broadcasting으로 A를 sum_A로 나눌 수 있다.

A / sum_A

# Output
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
        [0.1818, 0.2273, 0.2727, 0.3182],
        [0.2105, 0.2368, 0.2632, 0.2895],
        [0.2222, 0.2407, 0.2593, 0.2778],
        [0.2286, 0.2429, 0.2571, 0.2714]])

어떤 축을 따라 A 원소의 누적 합을 계산하려면, 예를 들어 축 = 0(row by row)을 계산하면, cumsum function을 호출할 수 있다. 이 함수는 어떤 축에서도 입력 텐서를 감소시키지 않는다.

A.cumsum(axis=0)

# Output
tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  6.,  8., 10.],
        [12., 15., 18., 21.],
        [24., 28., 32., 36.],
        [40., 45., 50., 55.]])

2.3.7. Dot Products

가장 기본적인 연산 중 하나는 dot product 이다. x, y$∈ℝ^d$ 가 주어지면 dot product $x^Ty$ (or $<x, y>$) 는 같은 위치에 있는 원소의 곱에 대한 합이다. $x^Ty = \displaystyle\sum_{i=1}^{d}{x_iy_i}$

y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

# Output
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))

두 벡터의 dot product는 원소 곱셈의 합과 동일하게 표현할 수 있다.

torch.sum(x * y)

# Output
tensor(6.))

dot product는 다양한 상황에서 유용하다. 예를 들어, vector x$∈ℝ^d$와 가중치의 집합 w$∈ℝ^d$가 주어졌을 때, 가중치 w에 따른 x 값의 가중치 합계는 dot product $x^Tw$ 로 표현될 수 있다. 가중치가 음이 아니고 합이 1인 경우, dot product는 weighted average 를 표현하고 있다. 두 벡터를 단위 길이로 정규화한 후, dot product는 각도의 코사인 값을 표현한다. 우리는 이 섹션의 후반부에서 이 길이의 개념을 공식적으로 소개할 것이다.

2.3.8. Matrix-Vector Products

이제 어떻게 dot product를 계산하는지 알았으니, matrix-vector products 를 이해해보자. 행렬A 행 벡터로 시각화해보자.

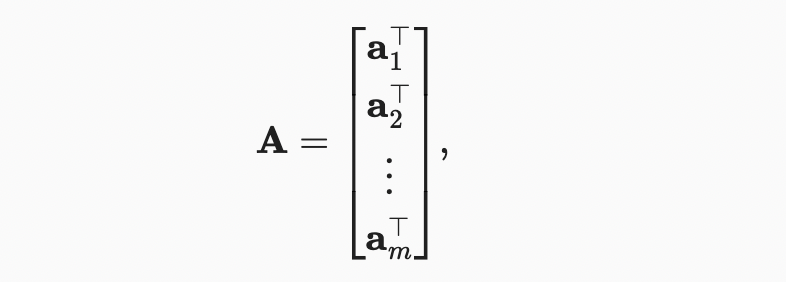
각 $a_i^T∈ℝ^n$는 행렬 A의 $i^{th}$ 행 벡터를 의미한다,

matrix-vector product Ax는 $i^{th}$ 요소가 dot product $a_i^Tx$인 길이 $m$의 열 벡터이다.

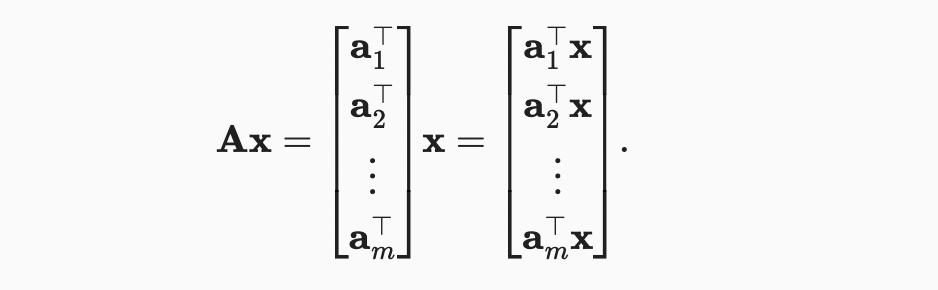
행렬 A$∈ℝ^{m \times n}$에 의한 곱셈은 $ℝ^n$에서 $ℝ^m$로 벡터를 투영하는 변환이라고 생각할 수 있다. 이러한 변환은 매우 유용하다. 예를 들어, 우리는 회전을 square matrix의 곱으로 나타낼 수 있습니다. 후속 장에서는, matrix-vector products를 사용하여 이전 계층의 값이 주어진 신경망에서 각 계층을 계산할 때 필요한 가장 집중적인 계산을 설명할 수 있다.

matrix-vector products를 코드에서 표현할 때 mv 함수를 사용한다. 행렬 A와 벡터 x로 구성된 torch.mv(A, x)를 부르면 matrix-vector product가 수행된다. A의 열 차원(length along axis 1)은 x의 차원(length)와 같아야 한다.

A.shape, x.shape, torch.mv(A, x)

# Output
(torch.Size([5, 4]), torch.Size([4]), tensor([ 14.,  38.,  62.,  86., 110.]))

2.3.9. Matrix-Matrix Multiplication

행렬 A$∈ℝ^{n \times k}$ 와 행렬 B$∈ℝ^{k \times m}$

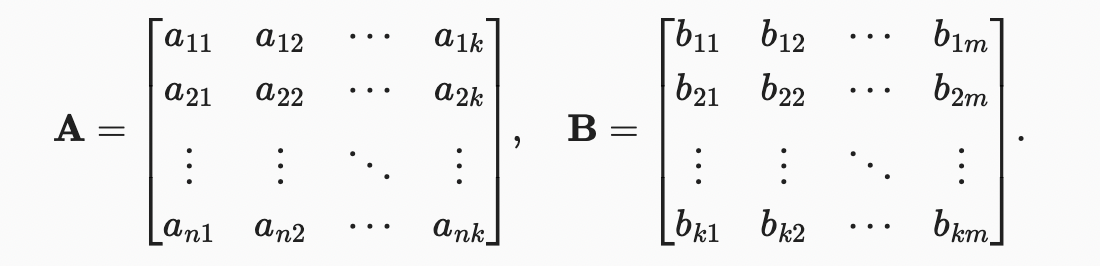
행렬 곱을 간단하게 표현하기 위해 A를 행 백터 B를 열 벡터로 생각하자.

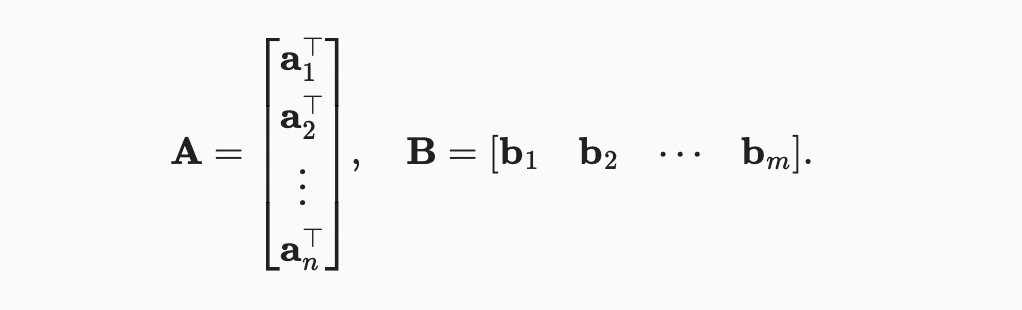
행렬 곱 연산 C$∈ℝ^{n \times m}$은 각 요소 $c_{ij}$를 dot product $a_i^Tb_j$로 계산한다.

아래에서 A와 B에서 행렬 곱셈을 수행한다. 여기서 행렬A는 5개의 행과 4개의 열을 가지고 행렬B는 4개의 행과 3개의 열을 가진다. 곱셈 후, 우리는 5개의 행과 3개의 열을 가진 행렬을 얻는다.

B = torch.ones(4, 3)
torch.mm(A, B)

# Output
tensor([[ 6.,  6.,  6.],
        [22., 22., 22.],
        [38., 38., 38.],
        [54., 54., 54.],
        [70., 70., 70.]])

행렬-행렬 곱셈은 단순히 matrix multiplication이라고 하며, Hadamard product와 혼동해서는 안 된다.

2.3.10. Norms

선형대수학에서 가장 유용한 연산자 중 일부는 norms이다. 형식적으로 벡터의 norm은 벡터가 얼마나 큰지 말해준다. 여기서 size의 개념은 차원이 아닌 구성요소의 크리에 관한 것이다. 선형대수학에서 vector norm은 벡터를 스칼라에 매핑하는 함수 $f$이다. 어떤 벡터x가 주어져도 첫 번째 속성은 만약 우리가 벡터의 모든 요소를 상수 인자 $\alpha$로 스케일링한다면, 그것의 norm은 또한 동일한 상수 인자의 absolute value(절대값)으로 스케일링된다.:

두 번째 속성

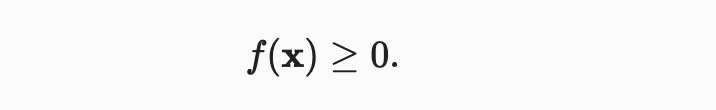
세 번째 속성

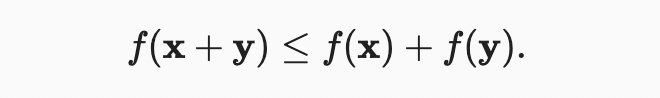
마지막 속성은 smallest norm이 달성되어야 하며 0으로만 구성된 벡터에 의해서만 달성되어야 한다.

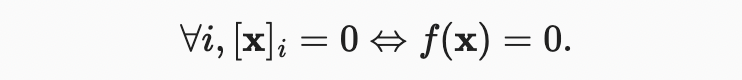
norms이 거리의 측정을 나타내는 것처럼 들리는걸 알아챘을 수도 있다. 그리고 만약 여러분이 초등학교에서 Euclidean distances(think Pythagoras’ theorem)를 기억한다면, 비-부정성과 삼각 부등식의 개념이 생각날 수도 있다. 사실 Euclidean distance가 norm이다.(구체적으로는 $L_2$ norm) n-차원 벡터 x의 원소들이 $x_1,...,x_n$이라고 가정하자.

x의 $L_2$ norm은 벡터 원소의 제곱합의 제곱근이다.

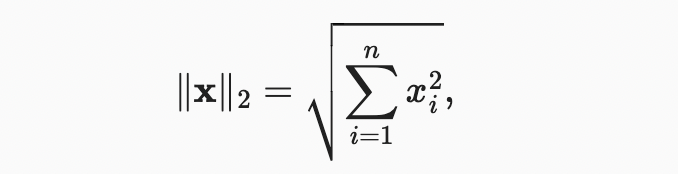
u = torch.tensor([3.0, -4.0])
torch.norm(u)

# Output
tensor(5.)

딥러닝에서는 squared $L_2$ norm을 많이 사용한다.

$L_1$ norm도 많이 보긴 할텐데, 벡터 요소들의 절대값의 합을 표현한다.

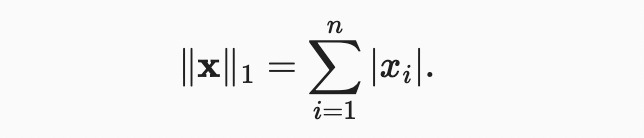
$L_2$ norm과 비교했을 때, outliers(특이치)의 영향을 덜 받는다. $L_1$ norm 계산을 위해, 우리는 절대값 함수를 원소에 대한 합으로 구성한다.

torch.abs(u).sum()

# Output
tensor(7.)

$L_2$ norm과 $L_1$ norm 모두 $L_p$ norm의 특별한 경우이다.

Frobenius norm은 행렬 원소의 제곱합 제곱근이다:

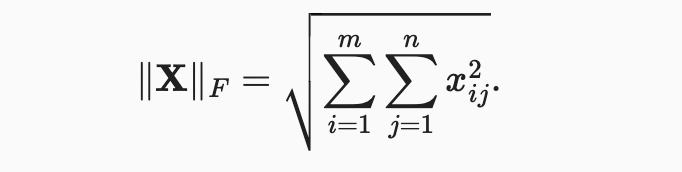
Frobenius norm은 벡터 규범의 모든 성질을 만족시킨다.

torch.norm(torch.ones(4, 9))

# Output
tensor(6.)

2.3.10.1. Norms and Objectives

딥러닝에서, 우리는 최적화 문제를 해결해야 한다: 관측된 데이터에 할당된 확률을 maximize하고 예측과 실제 관측치 사이의 거리를 minimize한다. vector representations을 items(예: 단어, 제품 또는 뉴스 기사)에 할당하여 유사한 items 간의 거리를 최소화하고 서로 다른 items 간의 거리를 최대화한다. 아마도 딥 러닝 알고리듬의 가장 중요한 구성 요소(데이터 외에)는 norms으로 표현된다.

2.3.11. More on Linear Algebra

2.3.12. Summary

• Scalars, vectors, matrices, and tensors are basic mathematical objects in linear algebra.
• Vectors generalize scalars, and matrices generalize vectors.
• Scalars, vectors, matrices, and tensors have zero, one, two, and an arbitrary number of axes, respectively.
• A tensor can be reduced along the specified axes by sum and mean.
• Elementwise multiplication of two matrices is called their Hadamard product. It is different from matrix multiplication.
• In deep learning, we often work with norms such as the $L_1$ norm, the $L_2$ norm, and the Frobenius norm.
• We can perform a variety of operations over scalars, vectors, matrices, and tensors.

2.3.13. Exercises

4. We defined the tensor X of shape (2, 3, 4) in this section. What is the output of len(X)? 2(first dimension)
5. For a tensor X of arbitrary shape, does len(X) always correspond to the length of a certain axis of X? What is that axis? axis = 0
6. Run A / A.sum(axis=1) and see what happens. Can you analyze the reason? It doesn't match( The size of tensor a must match the size of tensor b at non-singleton dimension 1
   )
7. When traveling between two points in Manhattan, what is the distance that you need to cover in terms of the coordinates, i.e., in terms of avenues and streets? Can you travel diagonally?
8. Consider a tensor with shape (2, 3, 4). What are the shapes of the summation outputs along axis 0, 1, and 2?
   axis 0 : torch.Size([3, 4])
   axis 1 : torch.Size([2, 4])
   axis 2 : torch.Size([2, 3])
9. Feed a tensor with 3 or more axes to the linalg.norm function and observe its output. What does this function compute for tensors of arbitrary shape?