논문 제목
InternImage: Exploring Large-Scale Vision Foundation Models with Deformable Convolutions (CVPR 2023)
URL: https://arxiv.org/abs/2211.05778
Github : https://github.com/OpenGVLab/InternImage
인용수 : 1,040회 (25.7.2 기준)

학부 때부터 Deformable Convolution Network(DCN)에 대해서 관심가지고 계속 연구를 진행해왔는데 그때는 v2가 가장 최신 방법이었지만 이젠 v3,v4까지 CVPR2023,2024를 통해 발표되었네요... v1,v2는 객체 탐지에 초점을 맞춘 반면 v3,v4는 CNN이 트랜스포머와 경쟁력이 있어서 다양한 다운스트림 태스크에 사용가능함을 시사했습니다.

다음 리뷰 논문은 DCNv4가 되겠군요..

Abstract

• 최근 몇 년간 대규모 비전 트랜스포머(ViTs)의 큰 발전과 비교할 때 컨볼루션 신경망(CNN) 기반의 대규모 모델은 여전히 초기 단계였음.
• 본 연구는 ViT처럼 파라미터 및 훈련 데이터 증가로부터 이득을 얻을 수 있는 InternImage라는 새로운 대규모 CNN 기반 파운데이션 모델을 제안함.
• InternImage는 Deformable Convolution을 핵심 연산자로 채택하여, 탐지 및 분할과 같은 다운스트림 작업에 필요한 넓은 effective receptive field을 가질 뿐만 아니라 입력 및 작업 정보에 의해 조건화되는 adaptive spatial aggregation을 가짐.

Proposed Method

Deformable Convolution v3

Convolution vs MHSA

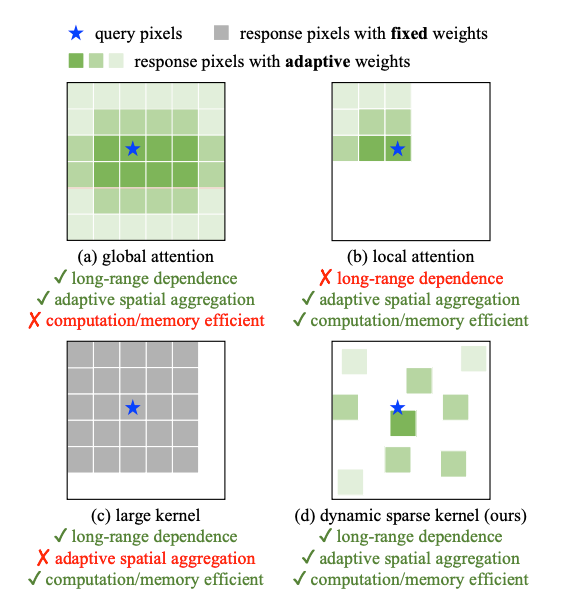
Long-range dependencies: CNN은 보통 작은 effective receptive field를 갖기 때문에 ViT처럼 장거리 정보를 학습하기 어려움.

Adaptive spatial aggregation: MHSA는 입력에 따라 동적으로 가중치를 학습하는 반면, 일반적인 컨볼루션은 고정된 가중치와 강한 inductive bias을 가지므로 범용성과 강건성이 떨어질 수 있음.

Revisiting DCNv2

컨볼루션과 MHSA 간의 격차를 해소하는 직접적인 방법은 컨볼루션에 long-range dependencies와 adaptive spatial aggregation를 도입하는 것임. 도입의 결과로 나온 것이 DCNv2이며 일반적인 컨볼루션의 확장 형태이다. 주어진 입력에 대해서 기준위치 $p_0$에 대해 아래와 같이 정의됨.

여기서 $K$는 전체 샘플링 지점의 수를 나타내며, $k$는 각 샘플링 지점을 인덱싱함.
$\mathbf{w}_k \in \mathbb{R}^{C \times C}$는 k번째 샘플링 지점의 projection weight를 나타내고, $m_k\in \mathbb{R}$은 k번째 샘플링 지점의 modulation scalar를 의미하며 시그모이드 함수에 의해 정규화됨.

이 수식으로부터 알 수 있는건 기존 컨볼루션에서 장거리 의존성을 위해 샘플링 오프셋$\Delta p_k$는 유연하게 동작하여 단거리 또는 장거리 특성과 상호작용이 가능하고, adaptive spatial aggregation을 위해 오프셋과 모듈레이션 스칼라는 모두 학습가능하며 입력 x에 의해 conditioned됨.
DCNv2는 MHSA와 유사한 장점을 공유한다는 것을 알 수 있으며 저자는 이 연산자를 기반으로 대규모 CNN 기반 파운데이션 모델을 개발하게 된 동기가 되었다고함.

Extending DCNv2 for Vision Foundation Models

기존에는 DCNv2가 일반 컨볼루션의 확장 형태로 사용되었고, 일반 컨볼루션의 사전학습된 가중치를 불러와 성능을 향상시키기 위해 파인튜닝하는 방식이 보편적이었음. 그러나 이러한 방식은 처음부터 학습해야 하는 대규모 비전 파운데이션 모델에는 적합하지 않음. 본 논문에서는 이 문제를 해결하기 위해 아래와 3가지 방식으로 DCNv2를 확장함.

1) Sharing weights among convolutional neurons

기존 DCNv2에서는 일반 컨볼루션과 마찬가지로 각 샘플링 지점의 컨볼루션 뉴런마다 독립적인 선형 투영 가중치가 존재하며 이로 인해 파라미터 수와 메모리 복잡도는 샘플링 포인트 수에 비례하여 증가함. 이는 특히 대규모 모델에서 비효율성을 유발한다고함.

이를 해결하기 위해 저자는 Separable Convolution 아이디어를 차용하여, 가중치 $w_k$를 Depth-Wise와 Point-Wise 부분으로 분리한다고함. 여기서 Depth-wise 부분은 위치 정보를 갖는 $m_k$가 담당하고 Point-Wise 부분은 모든 샘플링 포인트에서 공유되는 가중치 $w$가 사용됨.

2) Introducing multi-group mechanism

Multi-head self-attention에서처럼 공간 집계 과정을 G개의 그룹으로 분할함. 각 그룹은 고유한 오프셋 $\Delta p_{gk}$ 및 모듈레이션 스칼라 $m_{gk}$를 가지며 하나의 컨볼루션 층 내에서도 서로 다른 spatial aggregation patterns을 학습할 수 있음. 이로 인해 더욱 강력한 표현을 얻을 수 있다고 한다.

3) Normalizing modulation scalars along sampling points

기존 DCNv2에서는 각 샘플링 지점에 대해 시그모이드로 정규화했기 때문에 스칼라의 총합은 0에서 1사이 범위에 속하고, 모든 샘플링 지점에서의 모듈레이션 스칼라 합은 고정되어 있지 않으며 0에서 K까지 변화할 수 있음. 이로 인해 모델 학습 시 DCNv2 계층에서 그래디언트가 불안정한 문제가 생김.

이러한 불안정성을 완화하기 위해 요소별 시그모이드 정규화를 샘플링 지점 기준 softmax 정규화로 변경했다고함. 소프트맥스를 사용하면 각 그룹의 변조 스칼라 합이 1로 제한되어서 다양한 스케일의 모델에서도 학습 과정을 더 안정적으로 만듦.

G는 집계 그룹의 총 개수임. (코드에서 Defalut 값은 4를 사용)
$g$번째 그룹에 대해 $w_g$는 위치에 무관한 projection weight를 나타내며, $C' = C/G$는 그룹의 채널 차원임.
$m_{gk}$는 g번째 그룹에서 k번째 샘플링 지점에 대한 모듈레이션 스칼라로 softmax를 통해 K차원 상에서 정규화됨.
$x_g$는 그룹 g에 해당하는 input feature임
$\Delta p_{gk}$는 g번째 그룹의 k번째 샘플링 지점 $p_k$에 대응되는 오프셋임.

일반적으로 DCNv3는 DCN 시리즈의 확장으로서 다음과 같은 세 가지 장점을 갖는다고함.

1. 일반 컨볼루션의 장거리 의존성 부족과 적응적 공간 집계의 한계를 보완.
2. MHSA 및 Deformable Attention 연산자와 비교했을 때 DCNv3는 컨볼루션의inductive bias을 유지하므로 더 적은 학습 데이터와 짧은 학습 시간으로도 효율적인 학습이 가능함.
3. Sparse sampling을 기반으로 하며 MHSA나 large kernel에서 사용되는 reparameterizing 기법들보다 계산 및 메모리 측면에서 더 효율적.

InternImage Model

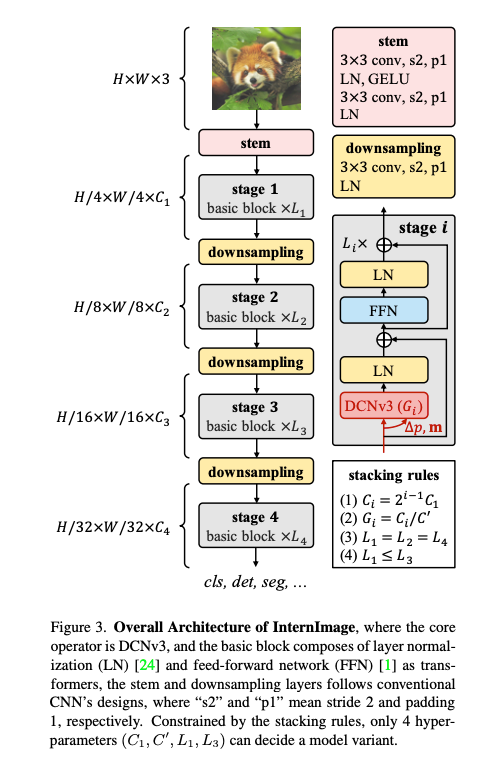
위 구조는 InternImage의 아키텍쳐이며 DCNv3를 핵심 연산자로 사용한 구조임.

Basic block

기존 CNN에서 널리 사용되던 bottleneck 구조와는 달리 제안하는 기본 블록은 Vision Transformer(ViT) 스타일에 더 가까운 구조이다.
이 블록은 Layer Normalization (LN), Feed-Forward Network (FFN), GELU 활성화 함수 등 최근 비전 태스크에서 효과가 입증된 고급 구성 요소들로 구성되어 있다.

블록의 핵심 연산자는 DCNv3이고 오프셋과 모듈레이션은 각각 3×3 Depthwise Convolution + 1×1 Pointwise Linear Projection의 separable convolution을 통해 예측한다.

기타 구성 요소는 기본적으로 Post-Normalization 설정을 따르며 Transformer 구조에서 사용하는 것과 동일한 방식으로 설계되었음.

Stem & downsampling layers

hierarchical feature map을 생성하기 위해 convolutional stem과 downsampling 계층을 사용하여 입력의 해상도를 점진적으로 축소함.

Stem 계층은 첫 번째 stage 전에 위치하며,
입력 해상도를 4배 줄이기 위해 2개의 컨볼루션, 2개의 LN, 1개의 GELU로 구성된다.
각 컨볼루션의 커널 크기는 3, stride는 2, padding은 1이며 첫 번째 컨볼루션의 출력 채널 수는 두 번째의 절반이다.

Downsampling 계층은 stage 사이에 위치하며,3×3 stride-2, padding-1의 컨볼루션 + LN으로 구성되어 피쳐 맵의 해상도를 2배 축소한다.

Experiment

본 논문에서는 제안한 InternImage 모델을 대표적인 비전 태스크들 (image classification, object detection, instance & semantic segmentation) 에서 최신 CNN 및 ViT들과 비교를 진행함.

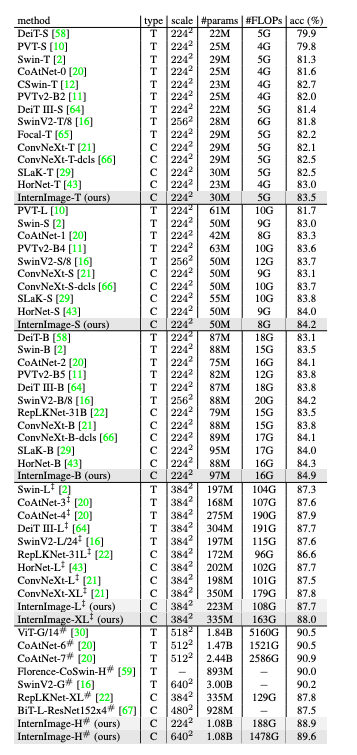
Image Classification

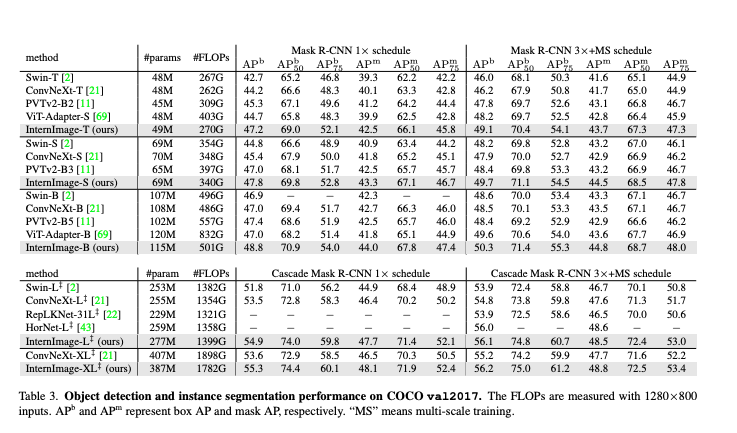
Ojbect Detection & Instance Segmentation

Semantic Segmentation

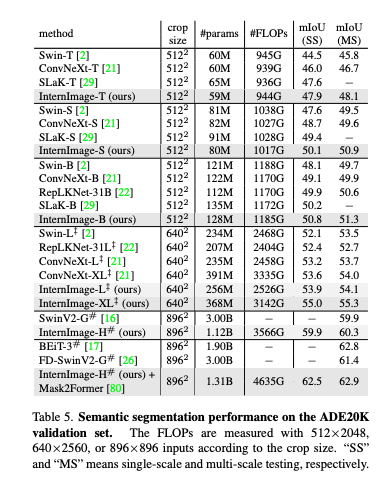
4가지 태스크에서 제안한 InternImage는 벤치마크 모델보다 우수한 성능을 보였음.

Ablation Study

대규모 모델에서는 연산자(DCNv3)의 파라미터 수와 메모리 사용량이 성능과 직결되며, 하드웨어 제약에 민감하다. 이를 해결하기 위해 DCNv3에서 컨볼루션 뉴런 간 가중치를 공유하도록 설계했음.

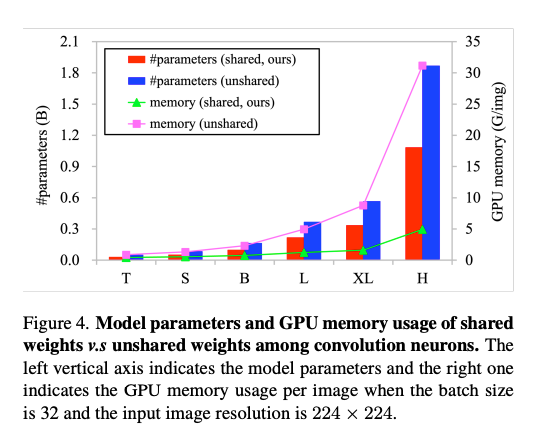
위 그림을 보면 가중치 공유 여부에 따른 파라미터 수와 GPU 메모리 사용량을 비교하였고, 공유하지 않을 경우 InternImage-H 스케일에서는 파라미터 수가 42.0% 증가 GPU 메모리 사용량이 84.2% 증가했다.

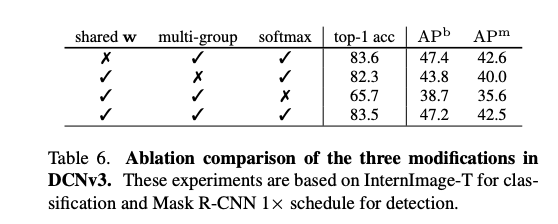
그럼에도 불구하고 InternImage-T 기준으로 shared / unshared 모델의 성능은 거의 동일하게 나타남.

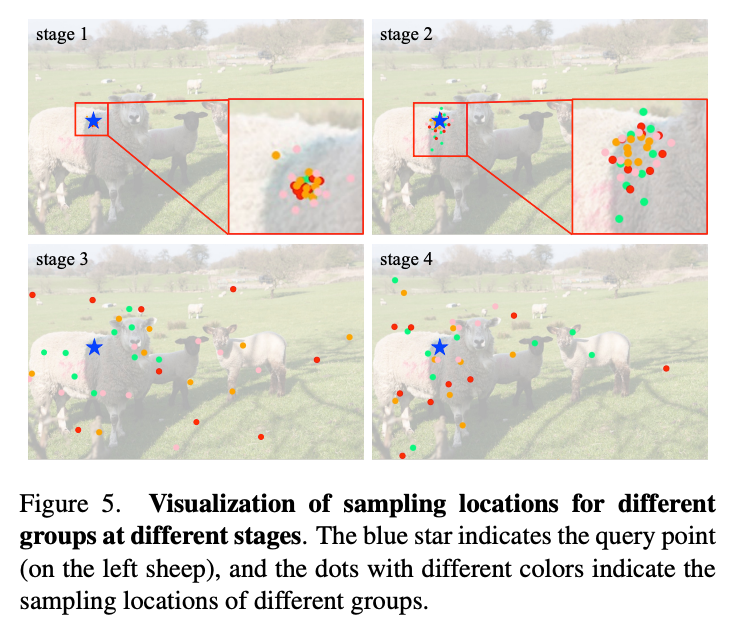
또한 Transformer처럼 공간 집계를 그룹으로 나눠 병렬로 수행함으로써 서로 다른 표현 공간에서 정보를 학습할 수 있도록 했다.
위 그림을 보면 동일한 query 위치에 대해 각 그룹별 오프셋이 다른 공간적 영역에 집중되어 있음을 보여줬다. 이는 각 그룹이 다양한 의미 정보를 학습했음을 의미한다.

그리고 Stage 1~2: ERF (Effective Receptive Field)는 국소적이고, Stage 3~4: ERF는 글로벌 수준까지 확장된다. 이는 ViT의 ERF가 항상 글로벌한 것과는 달리 점진적으로 확장되는 구조임을 보여줌.

Conclusion & Limitations

• 본 논문에서는 DCNv2 연산자를 조정하여 foundation model의 요구사항을 만족시키고, 이 핵심 연산자를 중심으로 블록, 스태킹 규칙, 스케일링 규칙을 적용한 InternImage 모델 제안.
• InternImage는 막대한 데이터로 학습된 잘 설계된 대형 비전 트랜스포머와 동등하거나 더 나은 성능을 낼 수 있음을 입증.
• DCN 기반 연산자들은 고속 처리가 요구되는 스트리밍 작업에 적응하는 데 있어 latency문제는 한계점으로 남아 있음.