백준 1655번 - 가운데를 말해요 (kotlin)

문제

https://www.acmicpc.net/problem/1655

유형

정렬, 자료구조, 우선순위 큐

풀이

요구 사항은 숫자를 입력받을 때마다 지금까지 받은 숫자들 중 중간(크기)값을 출력하는 것이다.

가장 먼저 매 입력을 리스트에 추가한 후 정렬하는 방법이 떠오른다. 정렬하는데 O(n * logn)이 소요되므로, 총 시간 복잡도는 O(n^2 * logn)이 된다. n<=100,000이므로, O(n^2)만 되어도 100억의 연산 횟수가 필요하여 시간 내에 답을 구할 수 없다.

어떤 방법이 또 있을까.. 나는 이 문제를 처음 접했을 때 내 힘으로 풀지 못했다. 다른 분들의 풀이를 참고했는데, 아이디어가 정말 독특해서 인상 깊었던 기억이 난다.

결론적으로 우선순위 큐(혹은 Heap 자료구조)를 2개 사용한다. Heap은 데이터를 저장할 때마다 O(logn)이 소요되지만, 기준에 대한 최소/최대 값을 O(1)로 가져올 수 있다. 우선순위 큐를 사용하는 방식은 다음과 같다.

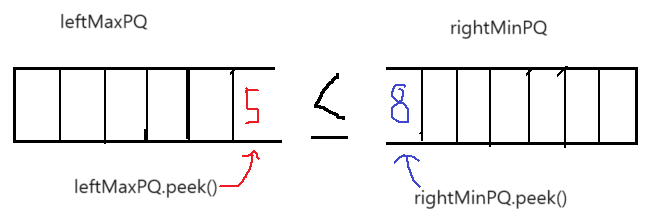
leftMaxPQ(최대우선순위큐)와 rightMinPQ(최소우선순위큐)를 사용한다. 그리고 숫자를 입력 받을 때마다 아래의 조건들을 지켜야 한다.

1. leftMaxPQ의 모든 숫자 <= rightMinPQ의 모든 숫자
2. 지금까지 입력받은 숫자가 짝수 개일 경우, leftMaxPQ.size = rightMinPQ.size
3. 지금까지 홀수 개를 입력 받았을 경우, leftMaxPQ.size = rightMinPQ.size + 1

이렇게 진행할 경우, leftMaxPQ의 최대값이 항상 전체의 중간 값이 된다.
왜냐면 짝수 개일 경우에는 leftMaxPQ.peek()은 rightMaxPQ의 모든 수보다 작거나 같고 leftMaxPQ의 나머지 수보다 크거나 같다. 따라서 2개의 중간값 중 하나가 된다(그림을 보면 더 잘 이해할 수 있다).
또한, rightMaxPQ.peek()도 비슷한 논리로 중간값 중 하나가 된다.
두 중간 값중 더 작은 것이 우리가 원하는 중간 값인데, 1번 조건에 의해 leftMaxPQ.peek() <= rightMaxPQ.peek()이므로 leftMaxPQ.peek()가 우리가 원하는 중간값이 된다.

홀수 개일 경우에도 비슷한 논리에 의해 leftMaxPQ의.peek()이 항상 중간값이 된다.

그러면 어떻게 매 입력마다 위 3가지 조건을 충족시키면서 큐에 숫자를 넣을 수 있을까?

짝수 개인 상태에서 새로운 숫자를 입력받는 경우:
-> rightMinPQ에 일단 넣고, rightMinPQ.peek()을 leftMaxPQ에 넣는다.
홀수 개인 상태에서 입력받는 경우:
-> leftMaxPQ에 일단 넣고, leftMaxPQ.peek()을 rightMinPQ에 넣는다.

그리고 leftMaxPQ.peek()을 확인하면 항상 중간 값을 찾을 수 있으며, 방금 이 알고리즘이 반영된 코드는 repeat문 안에서 확인할 수 있다.

코드 (kotlin)

import java.util.PriorityQueue

fun main() {
    val leftMaxPQ = PriorityQueue<Int>(compareByDescending { it })
    val rightMinPQ = PriorityQueue<Int>()
    val numberCount = readln().toInt()
    val stringBuilder = StringBuilder()

    repeat(numberCount) {
        if (leftMaxPQ.size == rightMinPQ.size) {
            rightMinPQ.offer(readln().toInt())
            leftMaxPQ.offer(rightMinPQ.poll())
        } else {
            leftMaxPQ.offer(readln().toInt())
            rightMinPQ.offer(leftMaxPQ.poll())
        }
        stringBuilder.append(leftMaxPQ.peek()).appendLine()
    }

    print(stringBuilder.toString())
}