백준 1106번 - 파일 합치기 (kotlin)

문제

https://www.acmicpc.net/problem/11066

유형

다이나믹 프로그래밍

풀이

minCost[i][j]: file[i ~ j]를 합치는 최소 비용
accCostSum[i]: file[1 ~ i]의 비용 합 (누적합)

전체 범위를 두 개의 부분 문제로 쪼개보자.

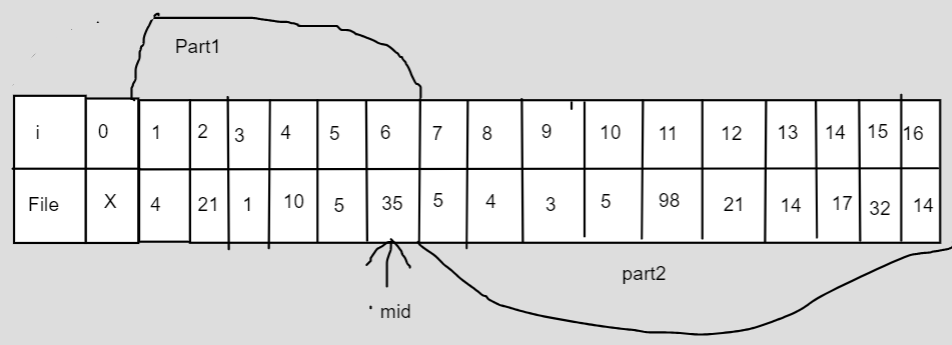
다음과 같은 수식을 얻을 수 있다.
minCost[1][n] = minCost[1][mid] + minCost[mid+1][n] + accCostSum[n]
두 범위에 대한 최소 비용을 각각 더하고 최종적으로 둘을 합치는 비용을 더한 것이다. (인덱스 1부터 시작하는 이유는 마지막에)

그리고 이렇게 쪼갠 문제는 다시 두 부분으로 나눌 수 있다.
minCost[mid+1][n] = minCost[mid + 1][mid2] + minCost[mid2 + 1][n] + accCostSum[n] - accCostSum[mid](file[mid ~ n]의 합)

이와 같이 모든 부분 문제를 두 부분으로 쪼개어나갈 수 있으며, 이것은 다이나믹 프로그래밍을 의미한다. 왜냐면 가장 작은 조각부터 해결해나가면 전체 범위의 답을 구할 수 있으며, 한 부분 문제가 여러 번 사용되기 때문이다!

Bottom-Up 방식을 이용할 경우 삼중반복문이 필요하다. 따라서, 시간 복잡도는 O(N^3)이다.

가장 바깥 반복문의 변수는 합칠 문제의 길이이다 예를 들어, file[4~9]를 합칠 거라면 extraLength는 인덱스 4를 제외한 [5~9] = 5가 된다. 그래서 부분 문제의 길이는 정확힌 1 + extraLegnth이다. 두 번째 반복문의 변수는 범위가 시작되는 인덱스를 뜻한다. 방금 예시에서 start는 4가 된다. 가장 안쪽 변수는 부분 범위 안에서 쪼개는 기준이 되는 인덱스이다.

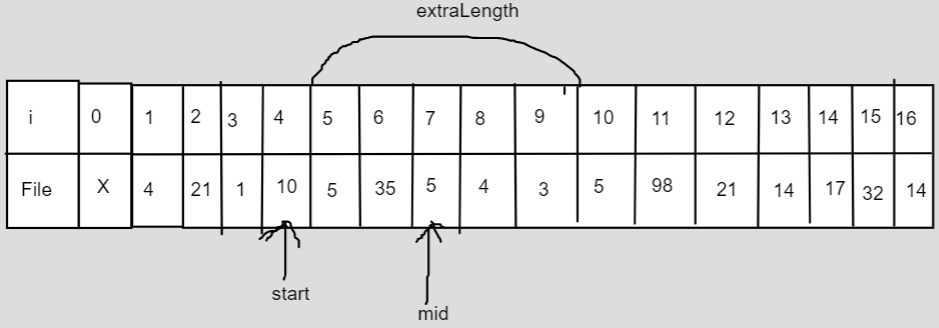
인덱스를 1부터 시작하는 이유는 accCostSum[0] 때문이다. 0부터 시작하면 file[0~5]의 비용 합을 구할 때 accCostSum[5] - accCostSum[-1]에 의해 인덱스 에러가 발생한다.

코드1 (Bottom-Up)

fun main() {
    val sb = StringBuilder()

    repeat(readln().toInt()) {
        val fileCount = readln().toInt()
        val fileCost = (listOf(-1) + readln().split(" ").map(String::toInt)).toIntArray()
        val accCostSum = IntArray(fileCount + 1)
        val minCostCache = Array(fileCount + 1) { IntArray(fileCount + 1) { Int.MAX_VALUE } }

        for (i in 1 ..fileCount) {
            accCostSum[i] = accCostSum[i - 1] + fileCost[i]
        }
        for (i in 1..fileCount) {
            minCostCache[i][i] = 0
        }

        for (extraLength in 1 until fileCount) {
            for (start in 1..fileCount - extraLength) {
                val end = start + extraLength
                for (mid in start until end) {
                    minCostCache[start][end] = minOf(
                        minCostCache[start][end],
                        minCostCache[start][mid] + minCostCache[mid + 1][end] + accCostSum[end] - accCostSum[start - 1]
                    )
                }
            }
        }

        sb.append(minCostCache[1][fileCount]).appendLine()
    }

    print(sb.toString())
}

코드2 (Top-Down)

lateinit var fileCost: IntArray
lateinit var accCostSum: IntArray
lateinit var minCostCache: Array<IntArray>

fun main() {
    val sb = StringBuilder()

    repeat(readln().toInt()) {
        val fileCount = readln().toInt()
        fileCost = (listOf(-1) + readln().split(" ").map(String::toInt)).toIntArray()
        accCostSum = IntArray(fileCount + 1)
        minCostCache = Array(fileCount + 1) { IntArray(fileCount + 1) { Int.MAX_VALUE } }

        for (i in 1 ..fileCount) {
            accCostSum[i] = accCostSum[i - 1] + fileCost[i]
        }

        sb.append(calculateMinCost(1, fileCount)).appendLine()
    }

    print(sb.toString())
}

fun calculateMinCost(start: Int, end: Int): Int {
    if (minCostCache[start][end] != -1) {
        return minCostCache[start][end]
    }

    if (start == end) {
        return 0
    }

    var minCost = Int.MAX_VALUE
    for (mid in start until end) {
        minCost = minOf(
            minCost,
            calculateMinCost(start, mid) + calculateMinCost(mid + 1, end) + accCostSum[end] - accCostSum[start - 1]
        )
    }

    minCostCache[start][end] = minCost
    return minCost
}