[논문] Adaptive Wing Loss for Robust Face Alignment via Heatmap Regression

Abstract

heatmap(hm) regression에 대한 이상적인 loss 함수를 제안한다. Adaptive Wing Loss(AWL)는 gt hm의 다른 타입들을 그 모양에 맞게 잘 적응하도록 한다. 이 “적응성”은 background보다는 foreground pixel들에 더 많은 패널티를 준다. foregorund와 background의 imbalance를 잘 다루기 위해서, foreground와 어려운 background에 더 많은 weight를 주는 방식인 Weighted Loss Map을 도입하였다. face alignment 분야에서 더 높은 정확도를 얻기위해 boundary prediction과 coordconv를 도입하였다.

Adaptive Wing Loss

• Loss function의 기본이론에서 시작해보면,
  • gt의 $y$값과 예측된 $\hat{y}$값이의 차이가 적으면 적은 영향력을, 크면 큰 영향을 가진다.
  • 따라서, 수렴에 도달했을때, 모든 error의 영향력은 균형을 이루게 되고, positive error에는 큰 경사도 크기(gradient magnitude)를 가지게 되고 negative error는 그 균형을 맞추기 위해서 작은 영향력을 가진다.
  • gaussian으로 만들어진 히트맵은 localization에 있어서 굉장히 중요한데, foreground에 집중되지 못한 학습결과는 픽셀의 intensity가 부족하게 되어서, 그역할을 잘 해내지 못하게된다.
• Wing Loss가 도입된 이유
  • MSE의 단점

    1. MSE는 small error에 둔감하여, gaussian 분포를 제대로 잡아내지 못한다.

    2. MSE는 모든 픽셀에 대해 같은 weight와 같은 loss함수로 계산되기 때문에 background 픽셀에 대한 계산이 압도적이게 된다.

    3. 최악의 경우, 히트맵의 강도가 약해져서 정확한 위치를 잡기 힘들어진다

       따라서, MSE로 학습하면 gt에 비해 넓고 흐릿한 히트맵을 예측하도록 하는 경향이 있다.

  • L1 Loss의 단점
    1. 작은 에러에서도 같은 영향력을 가지지만, 0에서 continous하지 않아, 수렴에 있어서, positive error를 가진 픽셀들의 수와 negative픽셀수가 정확히 같아야한다. 따라서 진동을 동반한 불안정한 학습이 될 수 밖에 없다.
  • 일반 Wingloss
    • 에러가 크면 constant한 gradient를, 작으면 큰 gradient를 가지기 때문에 작은 에러가 강화된다.
    • 하지만,
      1. background에서 small error가 발생한다해도 모으면 커지기 때문에, 차이가 0인 곳에서 L1보다 학습이 어려워진다.
    • 따라서, heatmap 방식에 바로 적용할 수 없다.
• Adaptive Wing Loss의 동작 방식
  • error가 크면 constant한 영향력을 가지게 하여 잘못된 annotation에 robust하게 한다.
  • 학습이 진행되며 loss가 작아지면서, 두가지 시나리오가 생긴다.
    1. foreground pixel에게는 영향력이 커지게 되면서, 이런 에러를 줄이고 충분히 좋아지면, 더 이상 건들지 않아 모델이 수렴할 수 있게 해준다.
    2. background pixel에서는 MSE처럼 작용해서 0에 가깝게 줄게 된다.
    • 고정된 loss(MSE, L1, …) 함수는 위의 두가지를 동시에 하지 못하는데, AWL은 가능하다기 때문에, 각각 다른 픽셀의 강도에 집중할 수 있다.
• Adaptive Wing Loss의 수식
  

• $A = \omega\frac{1}{1 + ({\theta}/{\epsilon})^{{\alpha}−y}}({\alpha}−y)\frac{{\theta}}{{\epsilon}}^{{\alpha}−y−1}\frac{1}{{\epsilon}}$

• $C=\theta A - \omega ln(1+(\frac{\theta}{\epsilon})^{\alpha-y})$

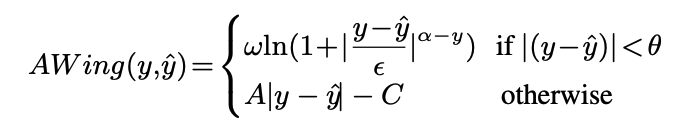
  • wing loss와는 다르게 $\omega$를 threshold로 사용하지 않고, $\theta$로 linear한 부분과 nonlinear한 부분을 구분하여 gt와 pred차이가 작으면 강한 영향력을 가지게 한다.
  • 더 중요한 것은 $\alpha-y$가 loss함수의 모양에 적응하여 0인 지점에서 smooth하게 해준다. 이때, y를 0과1사이에 값으로 만들기 위해서, $\alpha$는 2보다 살짝 크게 해서 $\alpha-y$가 1보다 살짝 크게해준다.
  • 그리고 윗부분이 wing loss처럼 에러를 작게 해준 후에는 MSE”처럼” 작동하게 된다.
  • 큰 $\omega$와 작은 $\epsilon$은 작은 에러에서의 영향력을 조절한다.
  • nonlinear한 부분에서는 Lorentzian loss과 비슷한데, 히트맵 특성상 gradient를 0까지 만들 필요는 없어진다. 어차피 annotation 자체가 사람이 한 것이기 때문에 아주 작은 약간의 오차는 허용하기 때문이다.