[논문] MeTRAbs: Metric-Scale Truncation-Robust Heatmaps for Absolute 3D Human Pose Estimation

이번 논문은 독일에서 나온 MeTRAbs: Metric-Scale Truncation-Robust Heatmaps for Absolute 3D Human Pose Estimation 입니다. 저는 이 분의 논문을 접하기 이전에 demo를 보고서, 너무 정확해서 한번 놀라고, 또한 코드를 직접 돌려보고 한번 더 놀랐는데요. 정말 역대급 정확성이라는 생각이 들 정도 였습니다.
우저자는 ECCV 3DPW Challenge에서 우승을 하신 분 입니다. 이 타이틀만 들어도 성능은 충분히 아실거라고 생각합니다.
그리고 논문에서 볼 수 있듯, 방법론을 정말 고민한 흔적이 명확하게 나타날 뿐만 아니라, 현존 public 데이터셋을 거의 다 끌어다가 쓰셨다는 것에 엄청난 열정과 대단함을 느낄 수 있었습니다.

https://arxiv.org/pdf/2007.07227.pdf
https://github.com/isarandi/metrabs

Introduction

저자는 이미지로 부터 3D reconstruction을 하는데, 여러가지 geometry ambiguties때문에 어려움이 있다는 문제를 시사합니다. 첫째로는, 다른 부분들이 같은 2D projection을 공유한다는 점. 두번째로는 카메라로부터 가까이 있는 작은 물체가 멀리있는 물체를 모델이 구분하기 힘들어하는 점을 지적하죠. 그리고 기존 기존 방법들이 이런한 문제를 명확하게 해결하지 못했다는 점을 꼬집으며 새로운 방법을 제안합니다. 그 방법의 main contribtution은 다음과 같습니다.

• main contribution:
  • pose estimation을 위한 새로운 3D heatmap 제안 (MeTRo)
    • input image와는 상관없이 정해져있는 scale
    • Human 3.6M과 MPI-INF-3DHP에서의 SOTA
    • 포즈의 일부가 잘리더라도 추론을 잘하는 높은 성능 (strong truncation-robustness)
  • coarse heatmap 해상도 ($8\times 8$)에서도 높은 정확도를 낼 수 있도록 하는 centered striding
  • MeTrabs
    • MeTRo와 같은 backbone에서 2D image-space heatmap도 추론하여 더 정확한 포즈를 reconstruction
  • monocular geometry 기반의 미분 가능한 정확한 pose reconstruction 모듈을 이용하여 마지막 GT에 대해 학습하는 end-to-end 모델
    • 거리 추정을 잘하는 것을 증명하고, strond & weak 관점에서의 recontruction variants를 광범위하게 평가

Single-Person Root-Relative Approach

이 섹션에서는 metric-scale root-relative 3D pose estimation 접근법에 대해서 이야기합니다. 아래 섹션에서 나오는 input과 output을 정리하고 가자면,

• input: 사람 객체가 crop된 이미지 $I\in R^{w\times h\times 3}$
• output: 3D skeleton
  • joint $J$의 좌표: $\{(\Delta X_j,\Delta Y_j,\Delta Z_j)^T\}^J_{j=1}$, mm 단위

Metric-Space Volumetric Heatmap Representation

우선, 기존 연구들에서 많이 사용하고 있는 volumetric heatmap 방법을 기반으로 합니다. 효과적인 stride $s$를 적용한 fully convolutional backbone 네크워크를 사용하려, $d\cdot J$의 spatial output chnnel을 가진 array를 만듭니다. 여기서, $d$는 추론한 volume의 depth 축에 따른 총 칸(discretization bins) 수를 의미합니다. 그리고, 그 array를 channel 축에 따라 $(w/s)\times(h/s)\times d$ volume을 $J$개 만듭니다. 다음은 각각의 volume에 3D spatial softmax가 적용되어, volumetric heatmap activations $V^{(j)\in R^{(w/s)\times(h/s)\times d}}$가 나오게 됩니다.
그럼, 어느 부분이 기존 방법과 다르냐! 바로, heatmap 축들이 3D joint 좌표가 고정된 scaling factor를 가진 soft-argmax를 적용하여, metric-scale 좌표로 나오는 부분입니다.

$\begin{bmatrix} \Delta X_j \\\\ \Delta Y_j \\\\ \Delta Z_j\end{bmatrix}=\sum V_{p,q,r}^{(j)}\cdot \begin{bmatrix} p\cdot s/w\cdot W \\\\ q\cdot s/h\cdot H \\\\ p\cdot s/d\cdot D \end{bmatrix}$

• $p,q,r$: 0부터 시작하는 volumetric heatmap array의 번호
• $W,H,D$: 추론된 완전한 volume의 크기로, width, height, depth을 의미, 고정된 값.
  • 논문에서는 2.2m (사람이 쭉 뻗어도 커버되는 사이즈)

위의 식은 denser striding으로 volume size가 바뀔 수 있기 때문에, 아래 Centered Striding섹션에서 나올 striding 방법에 따라 약간씩 조정되어야합니다. 참고로, 마지막의 root-rlative 추론 결과는 모든 조인트 위치로 부터 root 좌표를 뺀 값입니다. 즉, volume안에서의 추론된 root 좌표가 학습되는 것이 아니고 network는 추론된 volume안에 skeleton들을 위치할 수 있도록 합니다.
다시 말하면, camera calibration도 필요없고, skeleton의 사이즈를 재조정해야할 필요도 없는 방법으로, root와 다른 joint를 빼는 연산에만 backpropagation을 적용하게 되는 것이죠.

Architecture

기존 연구들처럼, upsampling하는 decoder와 refinement stage하는 것이 아니라, 저자들은 ResNet-50을 backbone으로 이용하여 다이렉트로 spatial heatmap을 추론합니다. 학습 중, ResNet-50은 $256\times 256$ 이미지에 32의 effective stride를 적용하여, $8\times 8$ 사이즈의 heatmap을 만들어냅니다. 그리고, 이때의 volumetric heatmap의 depth 사이즈는 8입니다. 하지만, single-person 데이터에서 평가할땐, 위의 방식으로 학습된 모델에 effective stride를 4로 설정하여 spatial한 64사이즈의 heatmap을 사용합니다. 이 방법은 dense prediction이라고 하고, image segmentation에서 많이 사용하는 방법입니다. 이런 방법은 일정 부분의 conv layer에서 striding이 없어지게 되고, 이어지는 conv의 dilation rate이 올라가게 합니다. 이 방법은 연산 필요가 늘어나는 만큼 정확도도 증가시키는데, 그래도 real-time 실행이 가능하게 합니다.

Centered Striding

train때와 달리 test에서 striding density를 바꾸게 될때, heatmap receptive field 중심의 분포가 어떻게 영향을 받는지가 중요합니다. Fig 3에서는 $256\times 256$ 이미지가 학습에는 stride가 32, 테스트에는 26이 적용됩니다.
soft-argmax는 weighted vote-averaging 방법이고, 고르지 못하게 voting되어 삐뚤어진 추론 결과를 나오게 됩니다. 이런 문제를 해결하기 위해서 도입된 것이 centered striding인데, backbone의 마지막 layer에 striding 방법을 반대로 적용하는 방법입니다. 그럼 결과가 이미지를 더 고르게 포함시키게 되는 것이죠.

Scale and Translation Agnostic 2D Loss

저자들은 capture studio에서 만들어진 3D 데이터 이외에도, MPII같은 in-the-wild 2D 데이터도 학습에 사용했다고 합니다.
미니 배치의 반을 2D label만 있는 데이터를 이용하였고, 2.5D heatmap에서는 straightforward하였습니다. 하지만 논문의 volume추론은 metric scale이고, image space에 정렬된 것이 아니기 때문에, scale과 transition에 상관없는 2D loss연산을 제안했습니다. 추론된 3D skeleton을 Z 좌표를 빼고 image plane에 project하여, loss연산전에 2D pixel ground truth에 맞추고, least-squares optimal fit하여 scaling을 맞추는 작업을 합니다. 이러한 alugnment layer는 미분 가능하여 gradient가 backpropagate할 수 있죠.

Truncated Pose Estimation

저자들의 metric-space heatmap는 heatmap boundary와 image boundary를 따로 두는데, 이 방법은 네트워크가 이미지가 잘리거나 크기조정된 경우에도 metric scale에서 완전한 포즈를 추론하도록 하여, joint가 이미지 밖으로 나가더라도 추론을 할 수 있게 합니다.

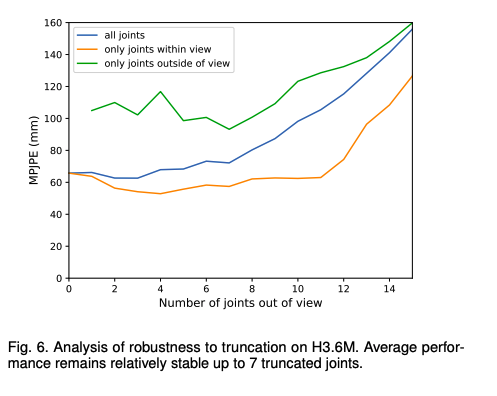
위의 Fig 7을 보면, 저자들의 방법이 유효함을 알 수 있습니다.

Training

• Loss: $L=L_{ann3D}+\lambda L_{ann2D}, \ L^1loss, \ \lambda =0.1$
• pretrained: ImageNet-pretrained weights
• Adam Optimizer with weight decay
• batch size: 64

Intuition

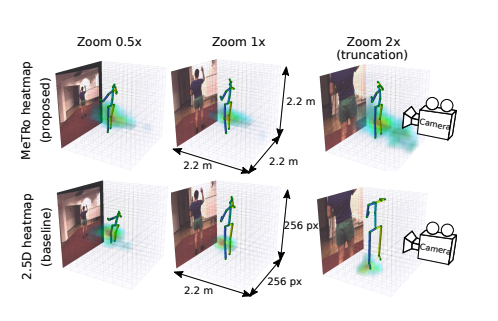
위의 Fig.4 에서는 저자가 개발한 모델이 이미지 scale과 truncation에 변함없는 결과를 추론함을 보여줍니다. 특히 hetmap의 가장 peak인 부분의 중간에 soft-argmax가 필요없다는 것을 알 수 있습니다. soft-argmax가 heatmap 중심에 적용되면, 먼거리에 있는 heatmap 값들도 영향을 받게되죠. 그러면 사람 중심이나 이미지의 사이드에 있을때, counter-balancing 보정 weight를 더해주어 모델값을 제대로 옮겨줄 수 있습니다. 그림의 마지막 행을 보면, 이미지에서 보이지 않더라도, 모델이 팔이 허리보다 위인 것을 추론할 수 있게 됩니다. 이런 결과들을 보면 conv network가 zero pad가 낀 conv로 위치정보를 encode할 수 있어 모든 skeleton을 volume안으로 넣을 수 있도록한다는 것을 알 수 있습니다.

Multi-person Absolute Pose Approach

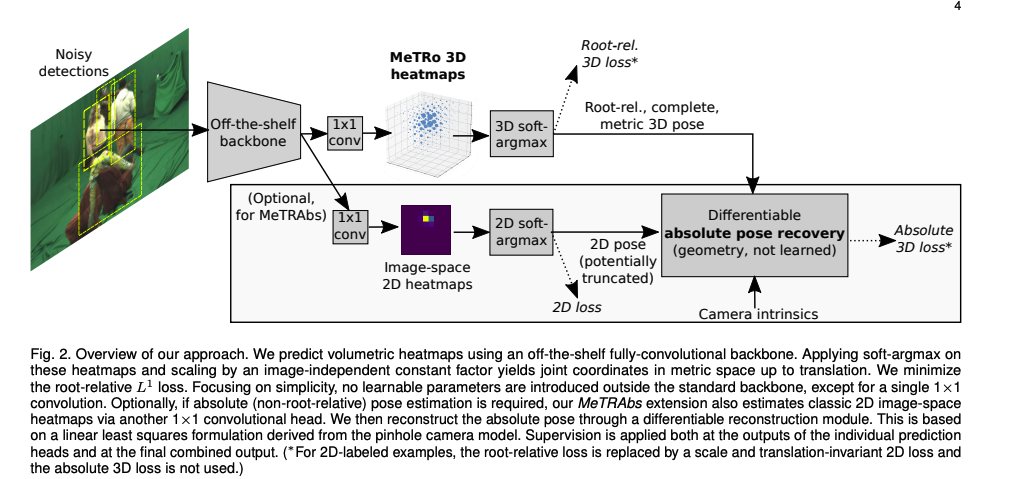
저자들은 위에서 설명한 3D pose estimation을 하는 MeTRo와 2D pose heatmap을 추론하는 기존의 연구 방법을 합하여, 완전한 3D pose를 추론하여 방법인 MeTRAbs을 제안합니다. 메인 아이디어는 MeTRo에서 scale을 어느정도 추정하는 부분을 거리를 추론하는데 사용하는 방법입니다.
image-sapce의 2D pose $\{(x_j,y_j)^T\}^J_{j=1}$ 추정을 더하여, 카메라 좌표계안에 완전한 3D pose를 만들기 위한 모든 필요한 정보를 얻는 것입니다. 다른 방법처럼 intrinsic parameter가 필요없는 이유는 root-relative 추정을 하기 때문입니다.
완전한 pose는 $\{(X_0+\Delta X_j,Y_0+\Delta Y_j,Z_0+\Delta Z_j)^T\}^J_{j=1}$으로 표현할 수 있는데, 이때의 $(X_0,Y_0,Z_0)$은 이 섹션에서 추정하려고 하는 완전한 pose offset 입니다.
우선, normalized image 좌표를 다음과 같이 구합니다.

• $(\tilde x_j, \tilde y_j)^T=K^{-1}(x_j,y_j)^T, K:$intrinsic matrix

그 후, full perspective pinhole camera 모델에서 reconstrunction하는 방법에서 기반하여 weak perspective method를 적용합니다. (weak perspective method)

• $\begin{bmatrix}\tilde x_j \\\\ \tilde y_j\end{bmatrix}=\begin{bmatrix}(X_0+\Delta X_j)/(Z_0+\Delta Z_j)\\\\ (Y_0+\Delta Y_j)/(Z_0+\Delta Z_j)\end{bmatrix}$

• $\begin{bmatrix}X_0-\tilde x_jZ_0 \\\\ Y_0-\tilde y_jZ_0\end{bmatrix}=\begin{bmatrix}\tilde x_j\Delta Z_j-\Delta X_j\\\\ \tilde y_j\Delta Z_j-\Delta Y_j\end{bmatrix}$

모든 joint를 고려할때, $(X_0,Y_0,Z_0)$에 대해 $2J$개의 linear equation을 가집니다. 그러나, $\tilde x, \tilde y, X, Y$는 모두 추정하는 것이기 때문에, 방정식을 구하기 쉽지 않습니다. 따라서, 저자는 Cholesky decomposition에 기반한 Tensorflow의 diffentiable solver를 이용하여 linear least squares로 해결하는 방법을 선택합니다. 이때의 differentiability는 loss $L^{abs3D}$를 적용하여 완전한 3D pose를 추정할 수 있도록 합니다.
근데 위의 식은 이미지안에 있는 조인트에 대한 2D heatmap을 예측하는 것이기 때문에, 이미지안에 있는 경우에만 적용할 수 밖에 없습니다. 그래서, 저자들은 한 stride 길이보다 이미지 보더에 가까운 곳을 예측할 수 있도록 optimization에서 joint들을 제외합니다. root joint를 reconstruct한 후에 두가지 방법으로 완전한 pose를 구합니다. 그 방법은 $(X_0+\Delta X_j,Y_0+\Delta Y_j,Z_0+\Delta Z_j)^T$을 구하거나, $(\tilde x_j, \tilde y_j,1)^T(\Delta Z_j+Z_0)$을 구하거나 입니다.
개별 prediction head와 마지막 완전한 결과 모두 L1 loss가 적용됩니다. root-relative MeTRo처럼, 저자는 MeTRAbs에서 2D labeled에 weak supervision 적용합니다. 그럼 전체적인 loss는 아래와 같게 됩니다.

• $L=L^{abs3D}_{ann3D}+L^{head3D}_{ann3D}+L^{head2D}_{ann3D}+\lambda(L^{head2D}_{ann2D}+L^{head3D}_{ann2D}), \ \lambda=0.1$

이 Loss를 적용하는데 있어서, 저자는 absolute loss를 적용하는 부분이 너무 빨리학습되어, 다른 부분에 안좋은 영향을 끼치는 것을 발견하고, 5000번의 update후에 absolute loss를 적용했다고 합니다.
또한, multi-person에서 real-time성능을 살리기위해서, MeTRAbs에는 dense prediction을 적용하지 않았다고 합니다.

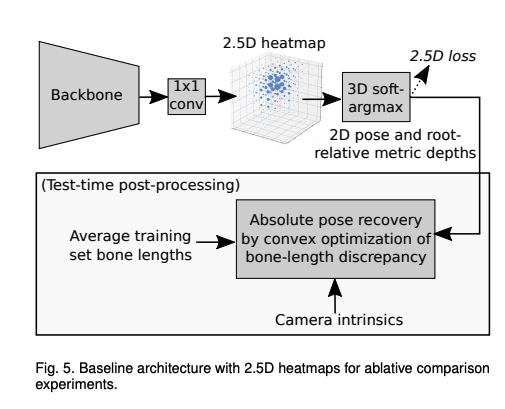
2.5D BaseLine

Datasets, Preprocessing,

• Datasets
  : H3.6M, MPII, 3DHP, MuCo, MuPoTS

• augmentation

  • geometric augmentations (scaling, rotation, translation, horizontal flip) and color distortion (brightness, contrast, hue, saturation)
  • synthesize (occlusion)

Results