과일 장수

문제 링크

📩 문제 설명

과일 장수가 사과 상자를 포장하고 있습니다. 사과는 상태에 따라 1점부터 k점까지의 점수로 분류하며, k점이 최상품의 사과이고 1점이 최하품의 사과입니다. 사과 한 상자의 가격은 다음과 같이 결정됩니다.

• 한 상자에 사과를 m개씩 담아 포장합니다.
• 상자에 담긴 사과 중 가장 낮은 점수가 p (1 ≤ p ≤ k)점인 경우, 사과 한 상자의 가격은 p * m 입니다.

과일 장수가 가능한 많은 사과를 팔았을 때, 얻을 수 있는 최대 이익을 계산하고자 합니다.(사과는 상자 단위로만 판매하며, 남는 사과는 버립니다) 예를 들어, k = 3, m = 4, 사과 7개의 점수가 [1, 2, 3, 1, 2, 3, 1]이라면, 다음과 같이 [2, 3, 2, 3]으로 구성된 사과 상자 1개를 만들어 판매하여 최대 이익을 얻을 수 있습니다.

• (최저 사과 점수) x (한 상자에 담긴 사과 개수) x (상자의 개수) = 2 x 4 x 1 = 8

사과의 최대 점수 k, 한 상자에 들어가는 사과의 수 m, 사과들의 점수 score가 주어졌을 때, 과일 장수가 얻을 수 있는 최대 이익을 return하는 solution 함수를 완성해주세요.

제한 사항

• 3 ≤ k ≤ 9
• 3 ≤ m ≤ 10
• 7 ≤ score의 길이 ≤ 1,000,000
  • 1 ≤ score[i] ≤ k
• 이익이 발생하지 않는 경우에는 0을 return 해주세요.

입출력 예제

k	m	score	result
3	4	[1, 2, 3, 1, 2, 3, 1]	8
4	3	[4, 1, 2, 2, 4, 4, 4, 4, 1, 2, 4, 2]	33

입출력 예 #2

• 다음과 같이 사과 상자를 포장하여 모두 팔면 최대 이익을 낼 수 있습니다.

사과 상자	가격
[1, 1, 2]	1 x 3 = 3
[2, 2, 2]	2 x 3 = 6
[4, 4, 4]	4 x 3 = 12
[4, 4, 4]	4 x 3 = 12

따라서 (1 x 3 x 1) + (2 x 3 x 1) + (4 x 3 x 2) = 33을 return합니다.

제출 답안

// 처음 답안
function solution(k, m, score) {
    // 점수가 큰 순으로 사과 정렬
    score.sort((a,b) => b - a);

    // m개씩 상자에 나누기
    let allBox = []
    let divide = ~~(score.length / m) + (~~(score.length % m) > 0 ? 1 : 0);
    for (let i=0; i<divide; i++) {
        allBox.push(score.splice(0, m));
    }
    
    
    let result = 0;
    allBox.filter(v => v.length === m).map(v => result+=(v[m-1]*m))
    
    return result;
}

처음 생각으로는 사과가 큰 순으로 정렬을 하고, m개씩 배열을 나눠서 allBox에 담고, 그 allbox를 filter()와 map()을 사용하는 방식이었다.

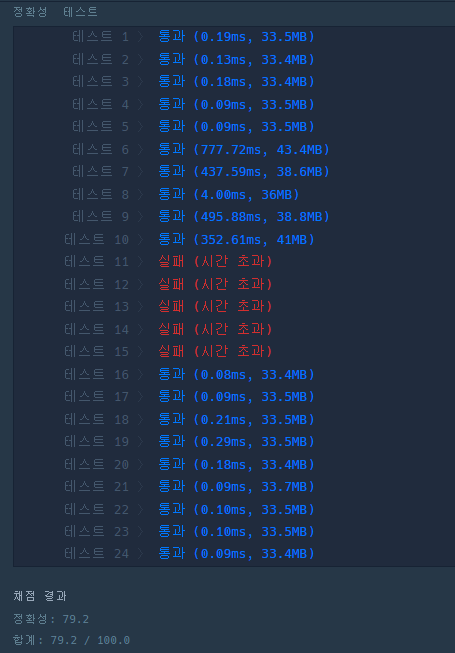
다만 시간 초과 에러가 떴는데 조건 중

7 ≤ score의 길이 ≤ 1,000,000

score의 최대 길이가 백만이라 그런지 시간 초과가 나왔다. 문제 난이도가 어려워질수록 제한 조건 때문에 테스트를 통과하지 못하는 경우가 많은 것 같다. 이제는 단순히 메서드를 사용하거나 구현을 통한 코딩 테스트 연습뿐만 아니라 알고리즘에 대한 공부를 시작해야할 것 같다!

시간을 줄일 수 있는 방법으로 새로 풀려고 했는데 아무리 생각해도 slice()가 아닌 방법은 떠오르지 않았다. 그나마 반복문의 횟수를 줄일 수 있는 방법으로 작성을 했는데 다행히 이 방법은 통과를 했다. 다만 전 코드와 비교했을 때 시간의 차이가 얼마나 나는지는 모르겠다. 알고리즘을 공부하자.

// 제출 답안

function solution(k, m, score) {
    // 점수가 큰 순으로 사과 정렬
    score.sort((a,b) => b - a);
    
    let result = 0;
    
    for (let i=0; i<score.length; i+=m) {
        
        let box = score.slice(i, i+m);
        
        if (box.length === m) {
            result += m*box[m-1];
        }
    }
    
    return result;
}

답안 설명

먼저 점수가 큰 순으로 정렬하고 반복문을 돌렸다. m개씩 새로운 배열 box에 담고, 그 길이가 m과 같을 때 result에다가 최대 이익을 추가하였다.