Test-Time Linear Out-of-Distribution Detection

• Publish: CVPR 2024
• Year: 2023
• LINK: https://openaccess.thecvf.com/content/CVPR2024/papers/Fan_Test-Time_Linear_Out-of-Distribution_Detection_CVPR_2024_paper.pdf

---

Summary

• 최근 OOD detection algorithms에 의해 만들어진 OoD score와 network feature 간의 linear trend 발견
• linear trend를 이용한 Robust Test-time Linear method (RTL) 제안
• simple linear regression를 test time adaptation로 사용하여 훨씬 더 정확한 OoD detection이 가능하도록 함
  

Method

Discussion of the Linear relationship

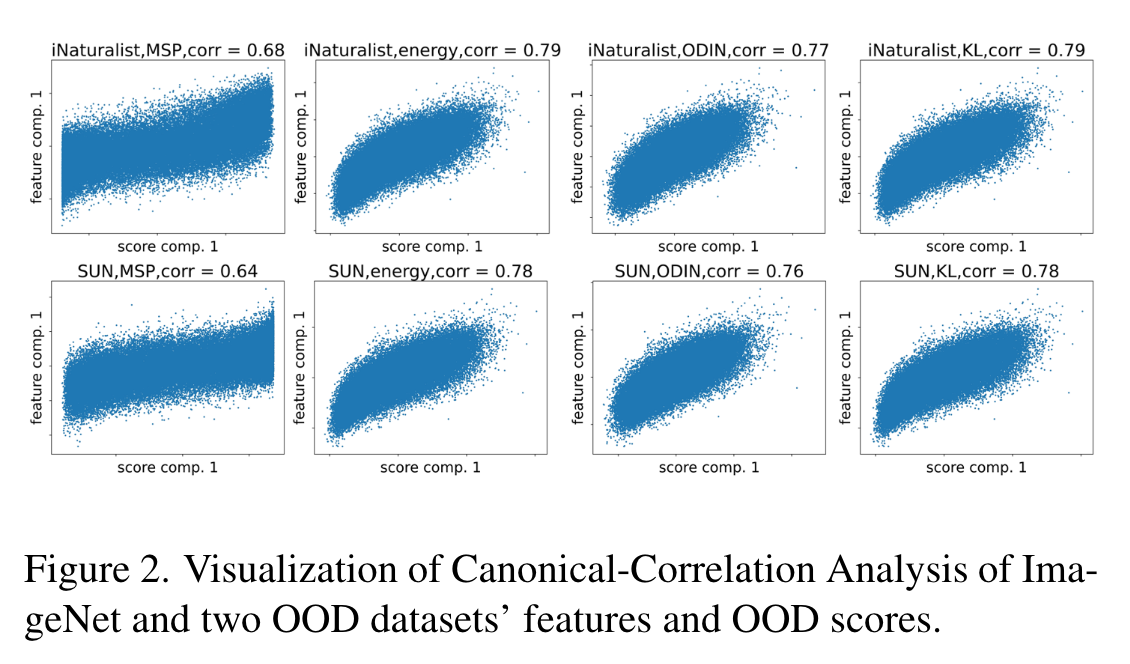
• canonical-correlation anaysis 사용
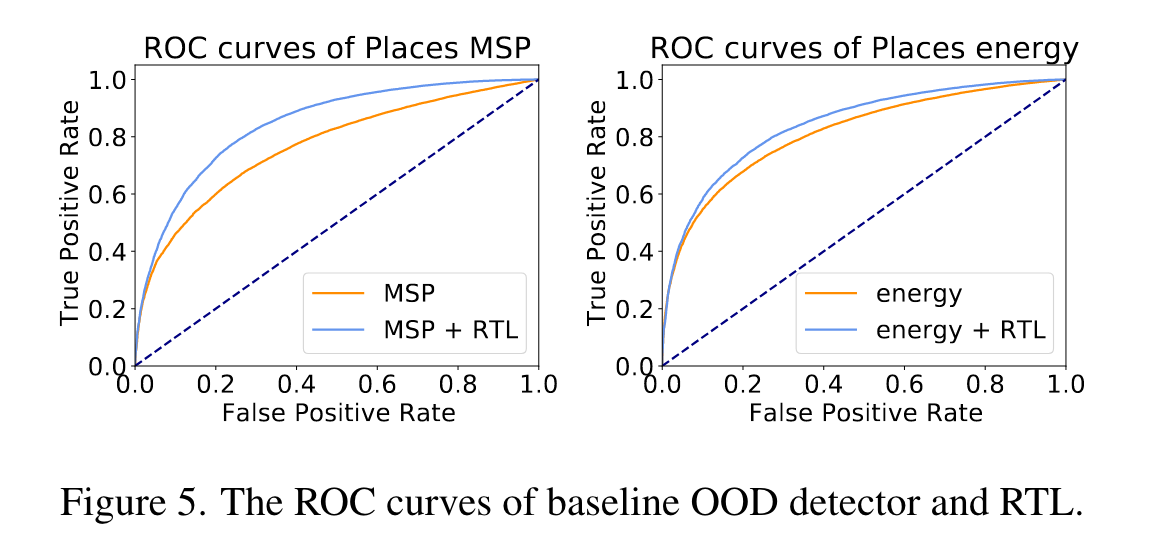
• OoD score가 서로 다른 algorithms에서 뽑혔어도 OoD score와 input feature 간에는 linear regression에 잘 맞는 것을 확인할 수 있음
• 하지만 위의 결과들은 single sample만을 다루었기 때문에 sample 간의 상호작용을 무시하는 경향이 있음 (sub-optimal한 algorithms)
• 즉, 미니 배치(전체) 테스트 데이터만 있으면 기준 OOD 방법을 크게 개선할 수 있음
• 모델의 overconfidence로 인해 부정확하게 inference 된 OoD score가 일부 존재하더라도 테스트 시 linear regression을 학습하면 이러한 score를 수정 가능

Mathematical Formulation

• Linear relationship

  $s = z^\intercal\beta + \epsilon$
  • Input image의 OoD score: $s := S(x)$
  • Input feature: $z$
  • $z^\intercal\beta$는 image $x$가 in/out distribution일지를 결정
  • $\epsilon$은 OoD detectors의 error
  • 즉 우리의 목표는 $(z_i, s_i)$의 feature-score pair를 이용하여 $\beta$를 추정하는 것

• 2개의 test-time linear training methods 제안

  • RTL(Robust Test-Time Linear Method): 중간 정도의 오류로 scoring 된 경우
  • RTL ++ : 매우 큰 정도의 오류로 scoring 된 경우

RTL (Robust Test-Time Linear Method)

• linear relation이 인식될만하면, 간단한 linear regression model로도 $\beta$를 추정하기에 충분함
  • †은 Moore-Penrose inverse를 의미
  • Moore-Penrose inverse: 일반적으로 역행렬은 정방행렬에서만 정의되지만, 역행렬이 아닌 경우에도 "유사 역행렬"을 정의할 수 있음

• 이러한 estimator를 통해 우리는 바로 어떤 instance $i$에 대한 OoD estimator를 제공할 수 있음
  $\hat{s}_{ours} = z_i^\intercal\hat{\beta}$

RTL++

• 만약 OoD scoring method가 제대로 작동을 하지 않는다면?
• 이럴 때를 대비해 만들어둔 case!

• explicit data-dependent variable $\gamma_i$를 이용하여 large error (OoD에 대한, not $\epsilon$이라는 error)
• $\gamma_i$ 가 0이 아닐 때, 이는 해당 샘플이 큰 오차를 가지고 있음을 의미
• 이러한 큰 오차를 가진 샘플들은 $\gamma_i$ 의 절댓값이 상대적으로 크게 나타남
• 이러한 $\gamma_i$를 통해 $\beta$를 추정하기 위해 아래와 같은 optimization을 취함
  $\min_{\beta,\gamma} \sum_{i=1}^n [\frac{1}{2}(s_i - z_i^\intercal\beta-\gamma_i)^2 + \lambda|\gamma_i|]$

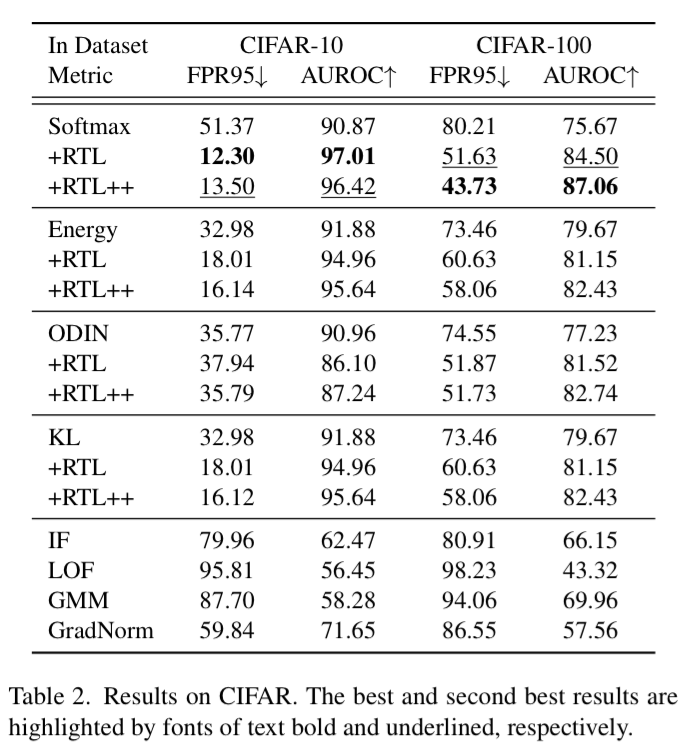
Experiments