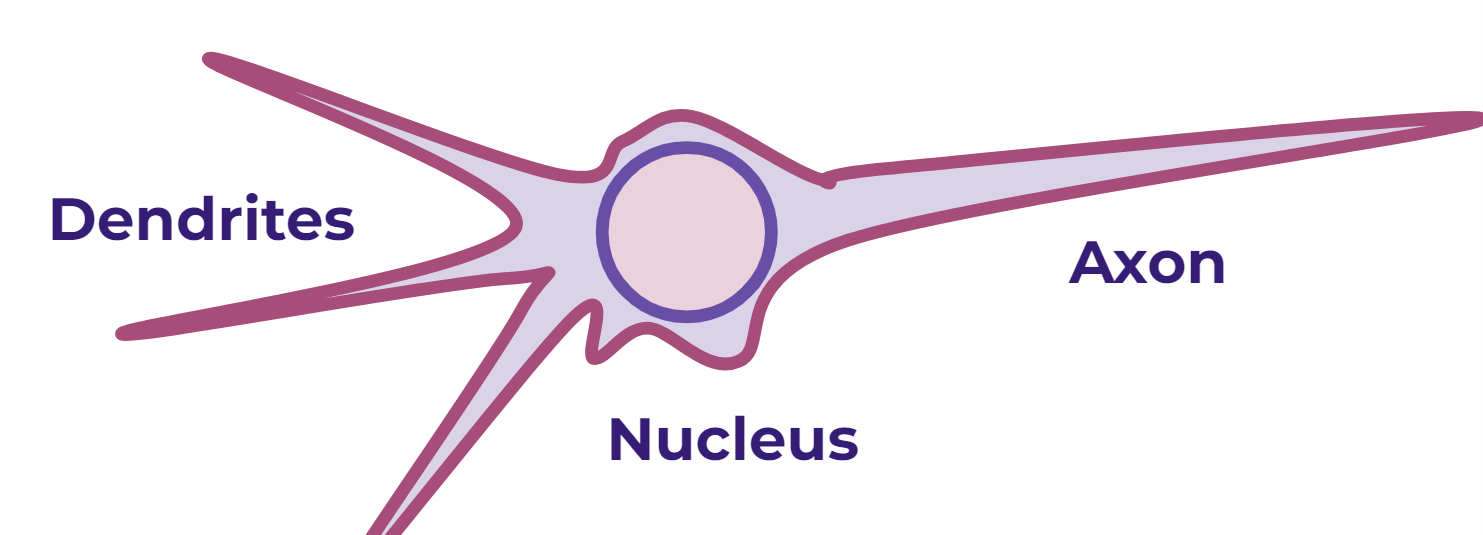
Biological Neurons

• Dendrites : inputs going into nucleus
• Nucleus : does the calculation
• Axon : passes output to other neurons
  

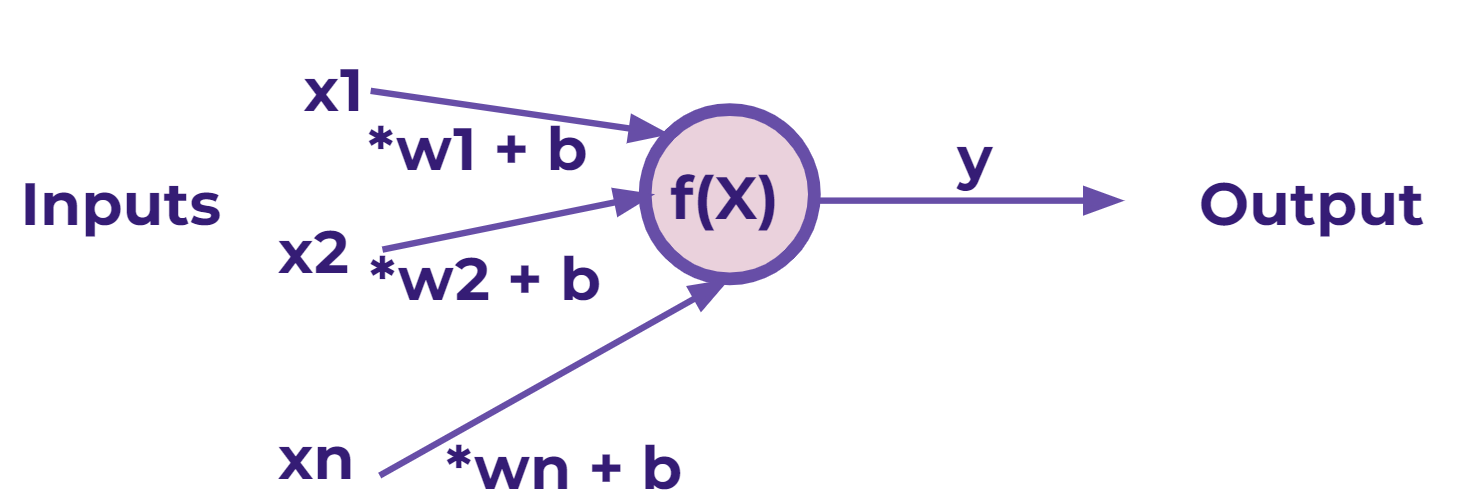
Perceptron Models

• Neural Networks mimic this model
  

• Generalized formula for perceptrons
  

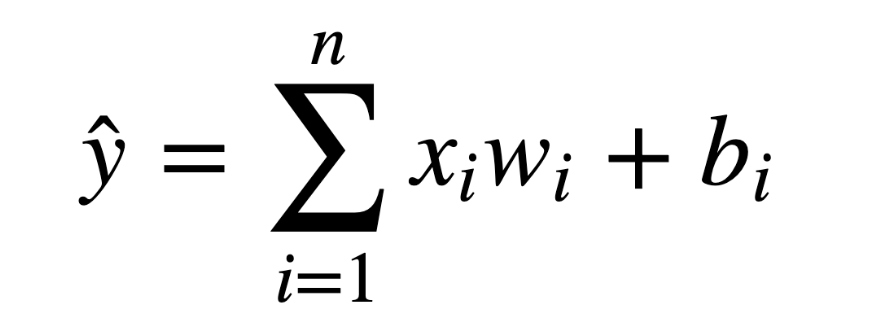
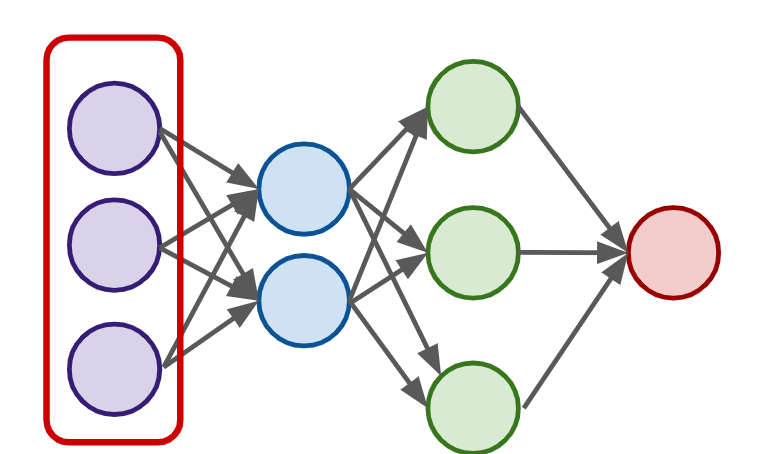
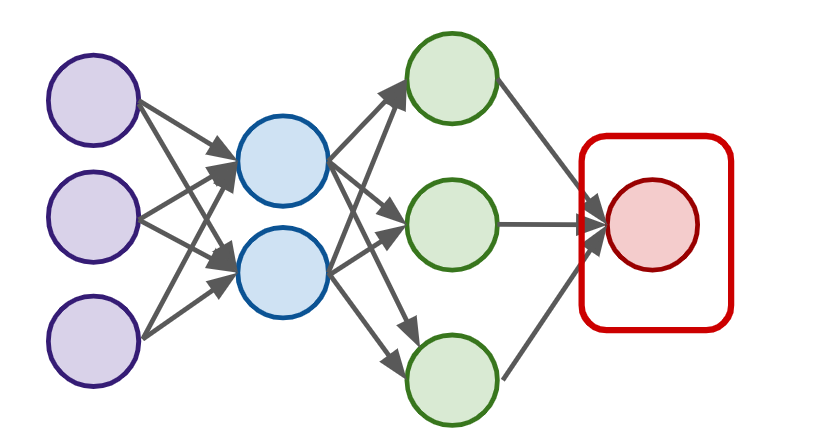
Neural Networks

• A single perceptron won’t be enough to learn complicated systems.

• To build a network of perceptrons, we can connect layers of perceptrons, using a multi-layer perceptron model.

• Input Layer
  

• Output Layer : final estimate of the output
  - There could be multiple output layers
  

• Hidden Layer : the layers in the middle
  - Deep Network : 2 or more hidden layers
  - Might be difficult to interpret

Activation Functions

• z = x*w + b : basic formula for each perceptron
  - w : how much weight or strength to give the incoming input
  - b : an offset value, making x*w have to reach a certain threshold before having an effect

• Activation Function (f(z) or X ) : sets boundaries to output values from the neuron

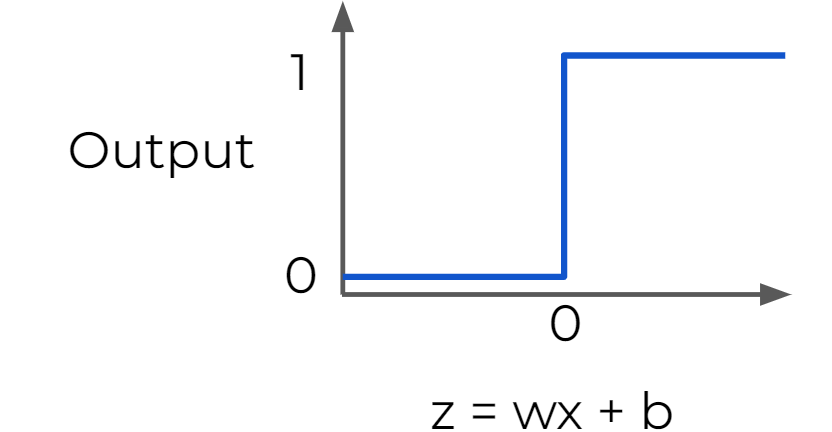
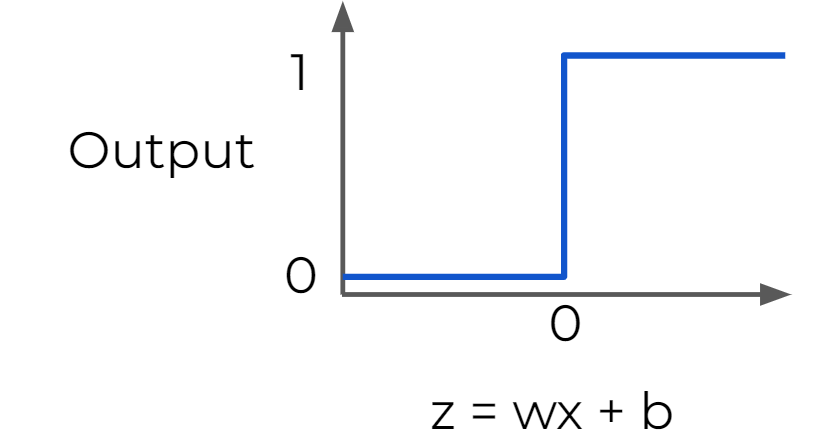
• Step Function : Useful for classification
  - a strong function - small changes aren't reflected
  

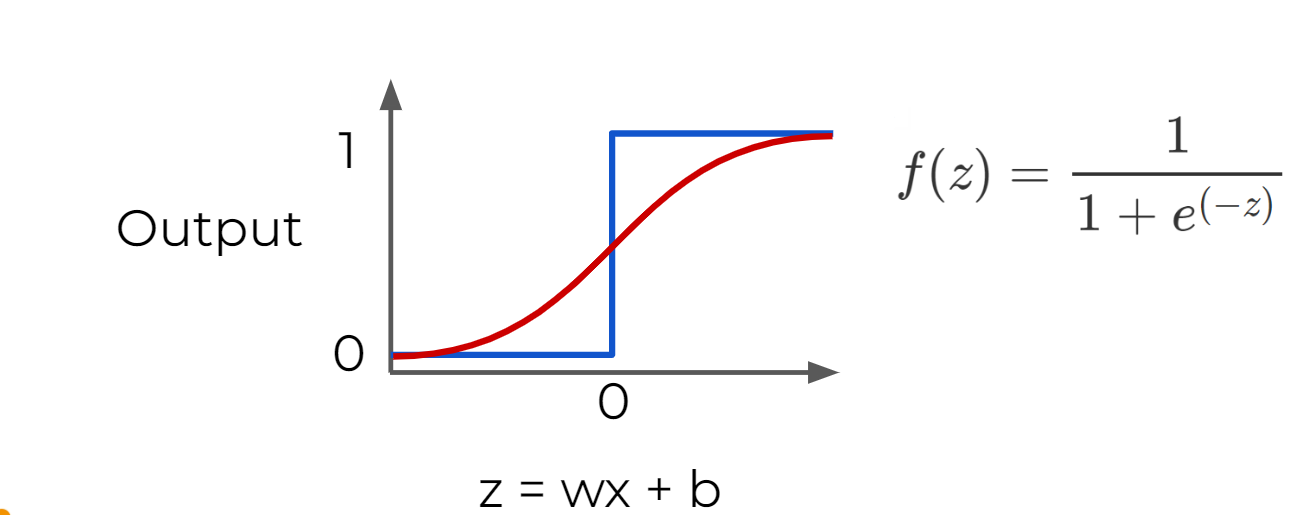
• Sigmoid Function : moderate form of a step function
  - more sensitive to small changes

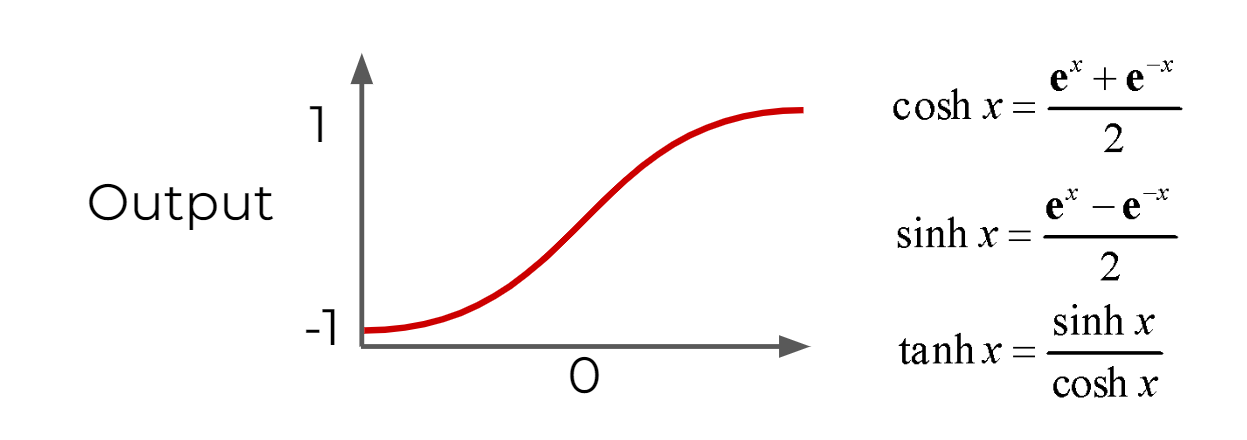
• Hyperbolic Tangent : outputs between -1 and 1
  

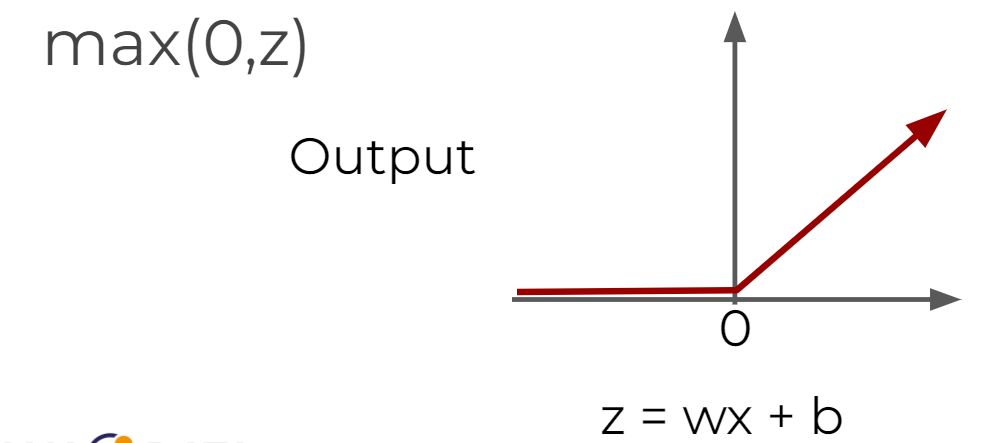
• Rectified Linear Unit (ReLU) : max(0,z)
  - deals with the issue of vanishing gradient
  - usually used as the default activation function
  

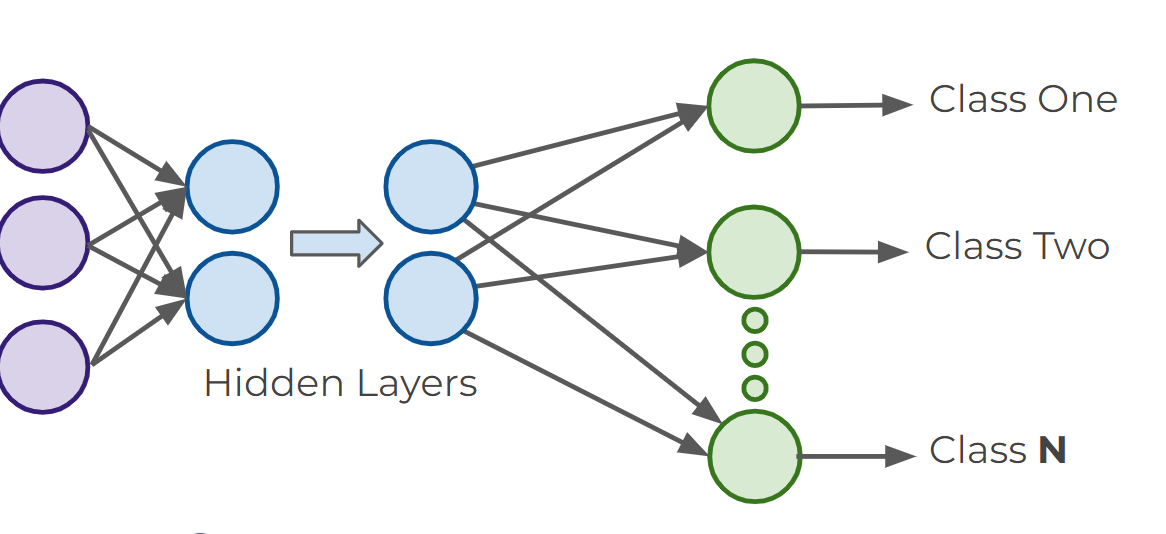
Multiclass Classifications

• There are 2 types of multi-class situations:
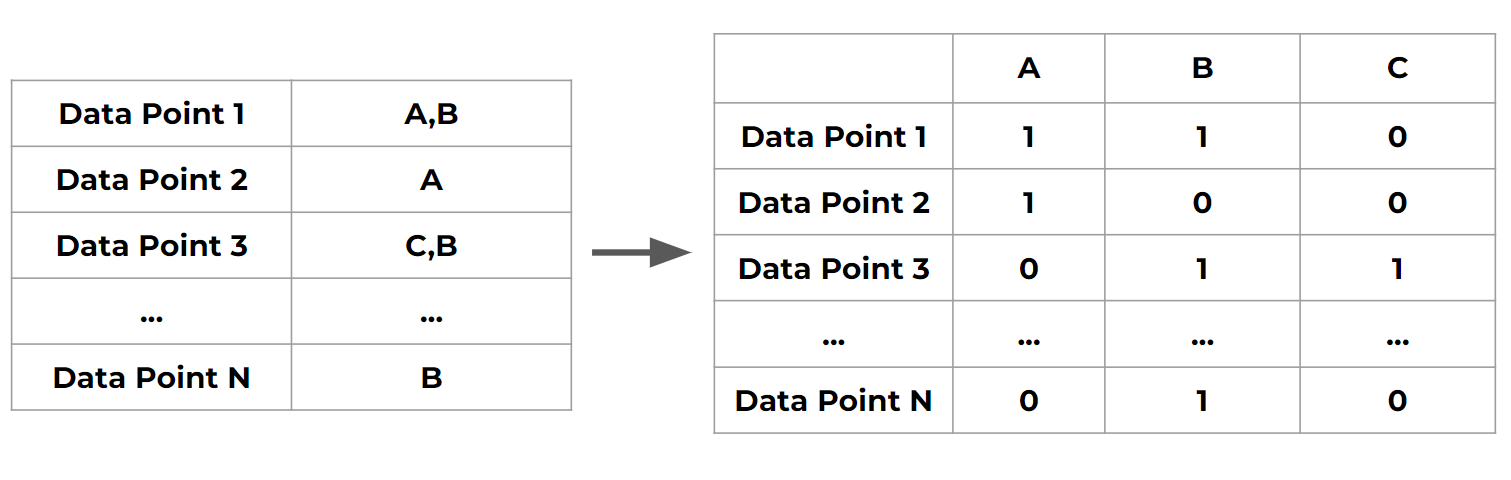
  - Non-exclusive classes : a data point can have multiple classes/ categories assigned to it (e.g. tagging photos )
  - Mutually Exclusive Classes : only one class per data point
  
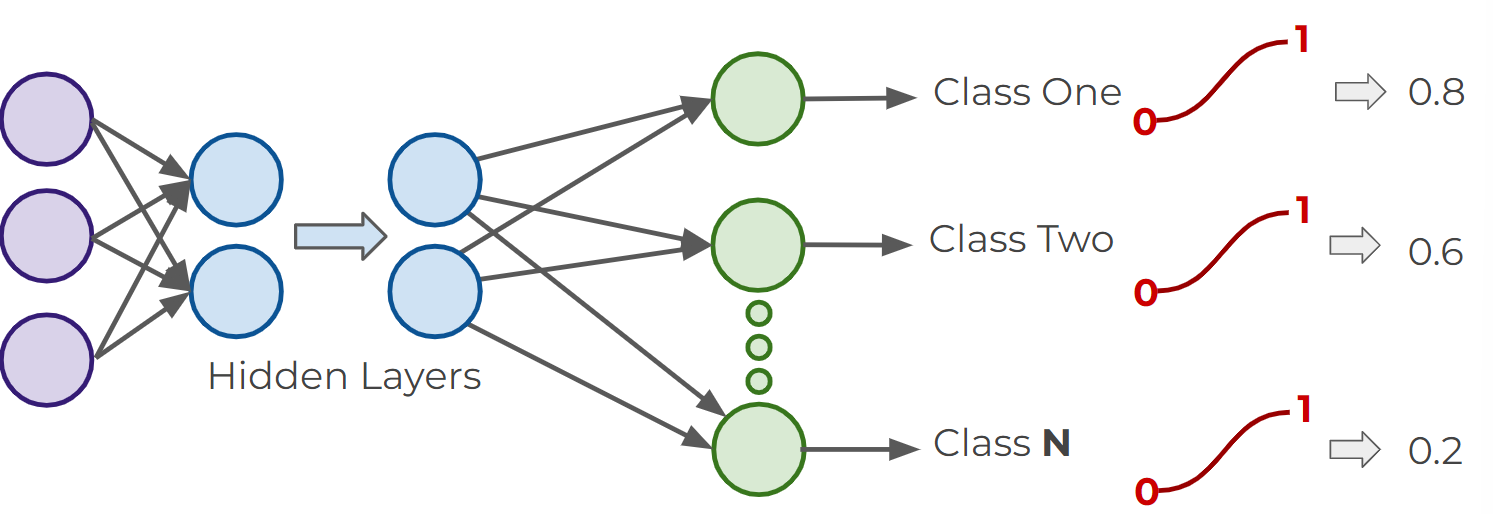
• For multiclass classifications, arrange multiple output layers
  

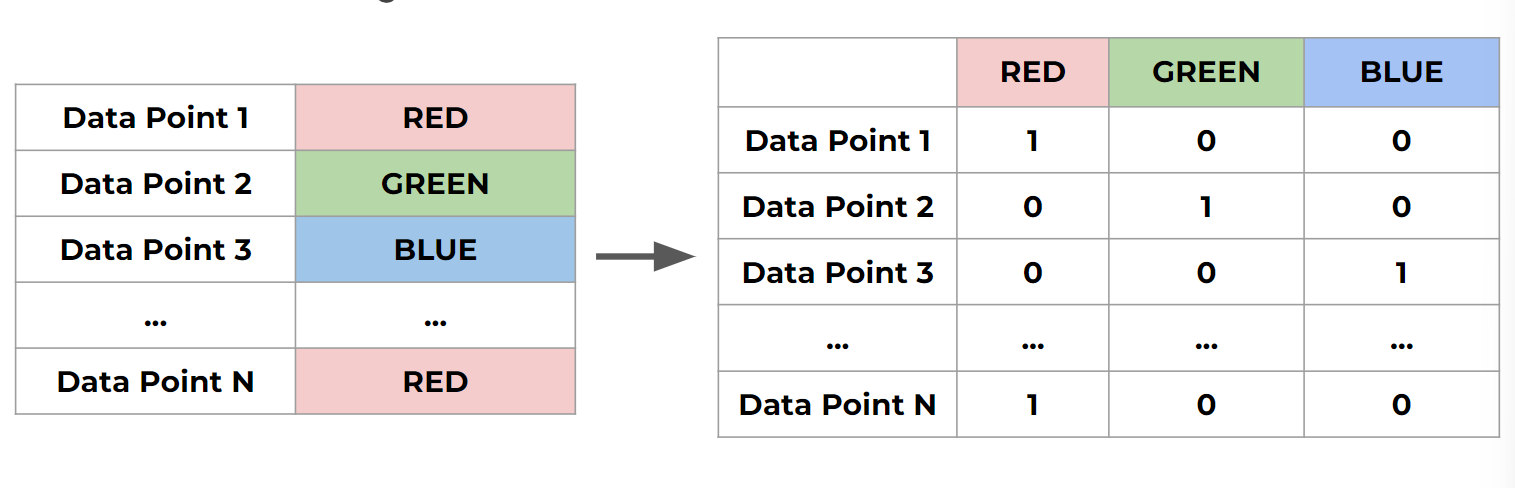
• One-hot encoding : how to turn classes into vectors
  - Mutually Exclusive Classes
  
  - Non-exclusive classes
  

• Activation functions for multiclass classification (Non-exclusive)
  

• Activation functions for multiclass classification (Exclusive)
  - Softmax Function : the target class chosen will have the highest probability
  

  

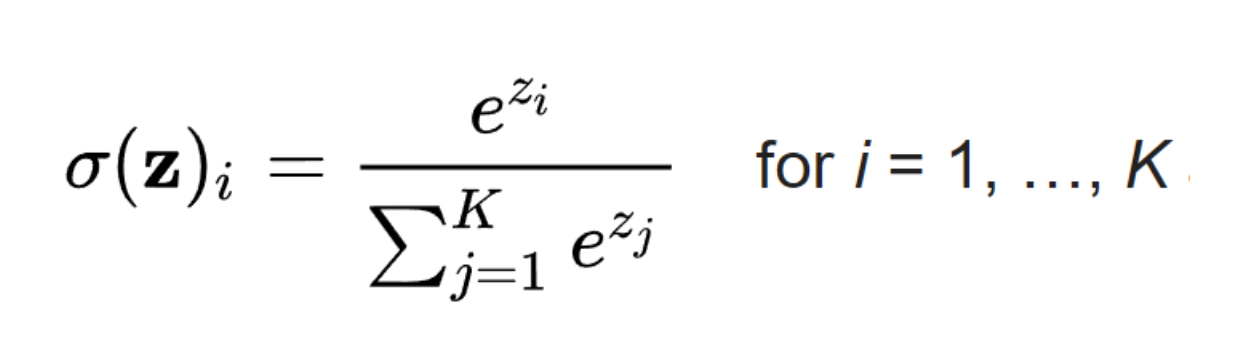
Cost Functions and Gradient Descent

• Notations
  - ŷ : estimation of what the model predicts the label to be
  - y : true value
  - a : neuron's prediction

• Cost Function
  - must be an average so it can output a single value
  - Used to keep track of our loss/cost during training to monitor network performance
  

• Quadratic cost function
  - aL is the prediction at L layer
  - Why do we square it?

  • punish large errors
  • keeps everything positive
    

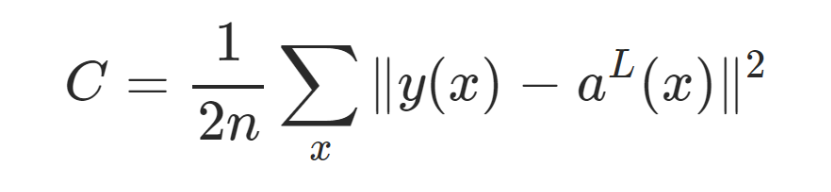
• Generalization of cost function
  - W is our neural network's weights, B is our neural network's biases, Sr is the input of a single training sample, and Er is the desired output of that training sample.
  

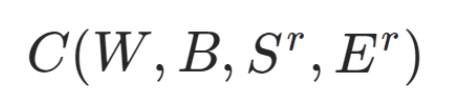
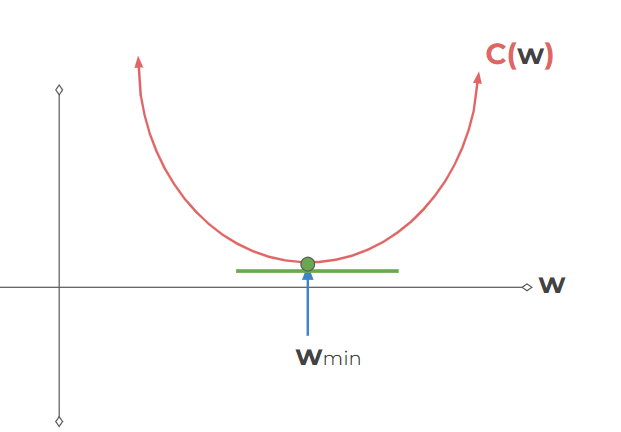
• Gradient Descent : find the w values that minimizes the cost
  - Learning Rate : how much you should move each time

  • Larger learning rates result in overshooting but lower computing rate
  • Adaptive Gradient Descent : We could adjust the step size in for each step
    

• Gradient : derivative for N-dimensional Vectors
  ∇C(w1,w2,...wn)
  

• Cross Entropy Loss Function : for classification problems
  - binary classfication :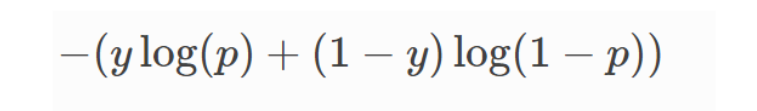
  - multi class classification :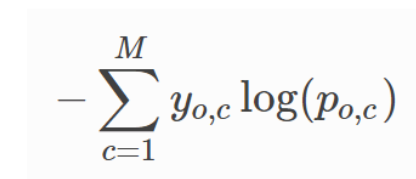

Back Propagation

• Usage of derivatives : find out how sensitive is the cost function to changes in w
  
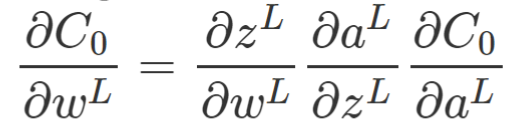
  - repeat the same for bias
  
• Back Propagation Process :
  - Step 1 : use input x to set the activation function a for the input layer & repeat
  
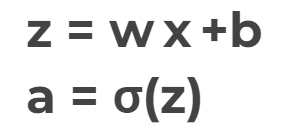
  - Step 2 : For each layer, compute
  
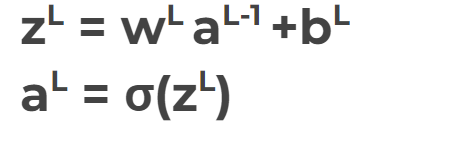
  - Step 3 : compute error vector