☄️ 이 글은 유튜브 나도코딩의 영상 / 한동대학교 이상산 교수님의 수업을 기반으로 쓰여졌습니다!
(업데이트 중)
지도 학습이란?
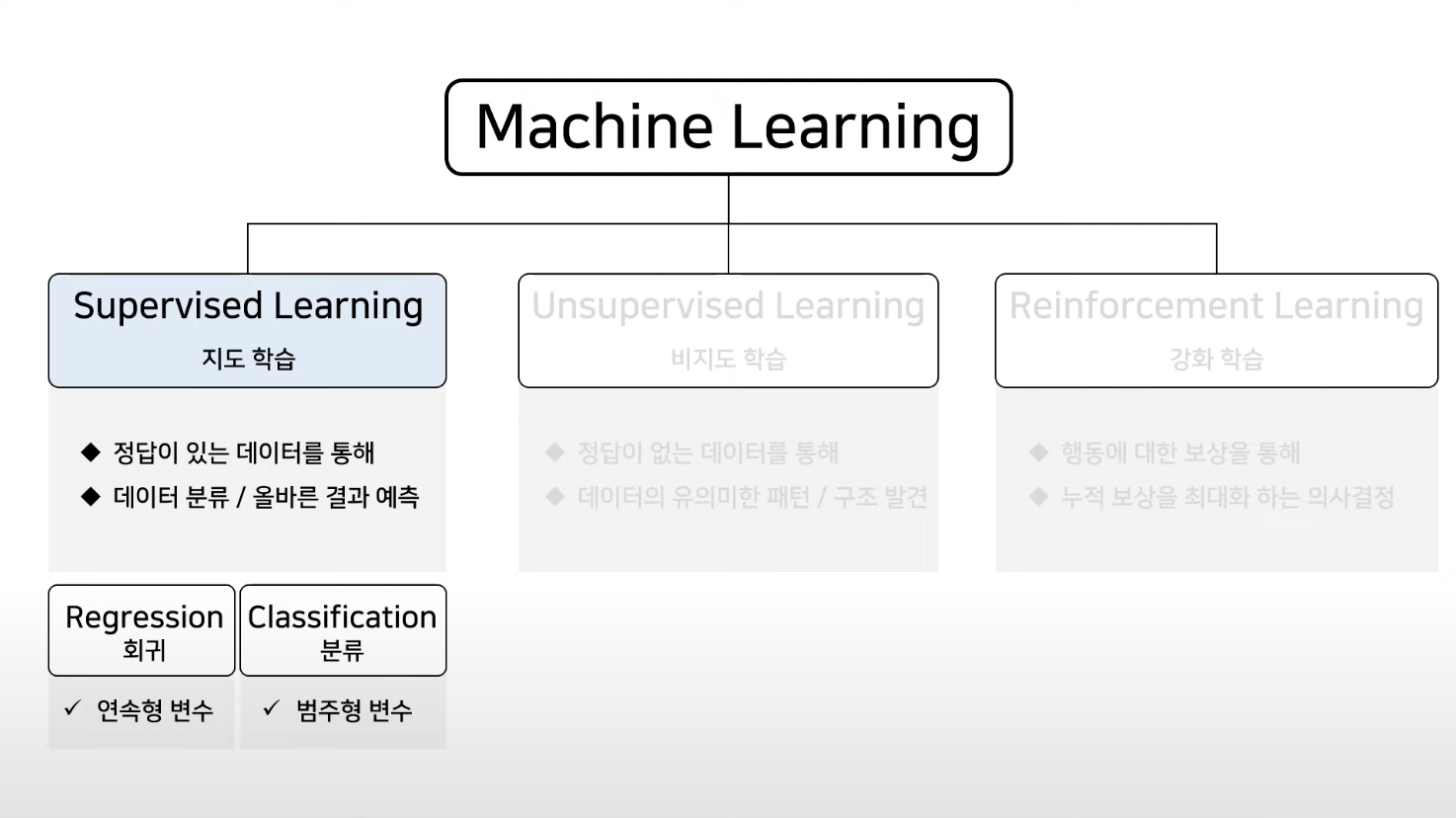
예측 또는 결정을 내리기 위해 레이블이 지정된 데이터에 대해 알고리즘을 훈련하는 기계 학습 기술이에요. 목표는 훈련 세트에 제공된 예제를 기반으로 입력을 출력에 매핑하는 기능을 학습하는 것이죠.
지도 학습의 유형
Regression 회귀
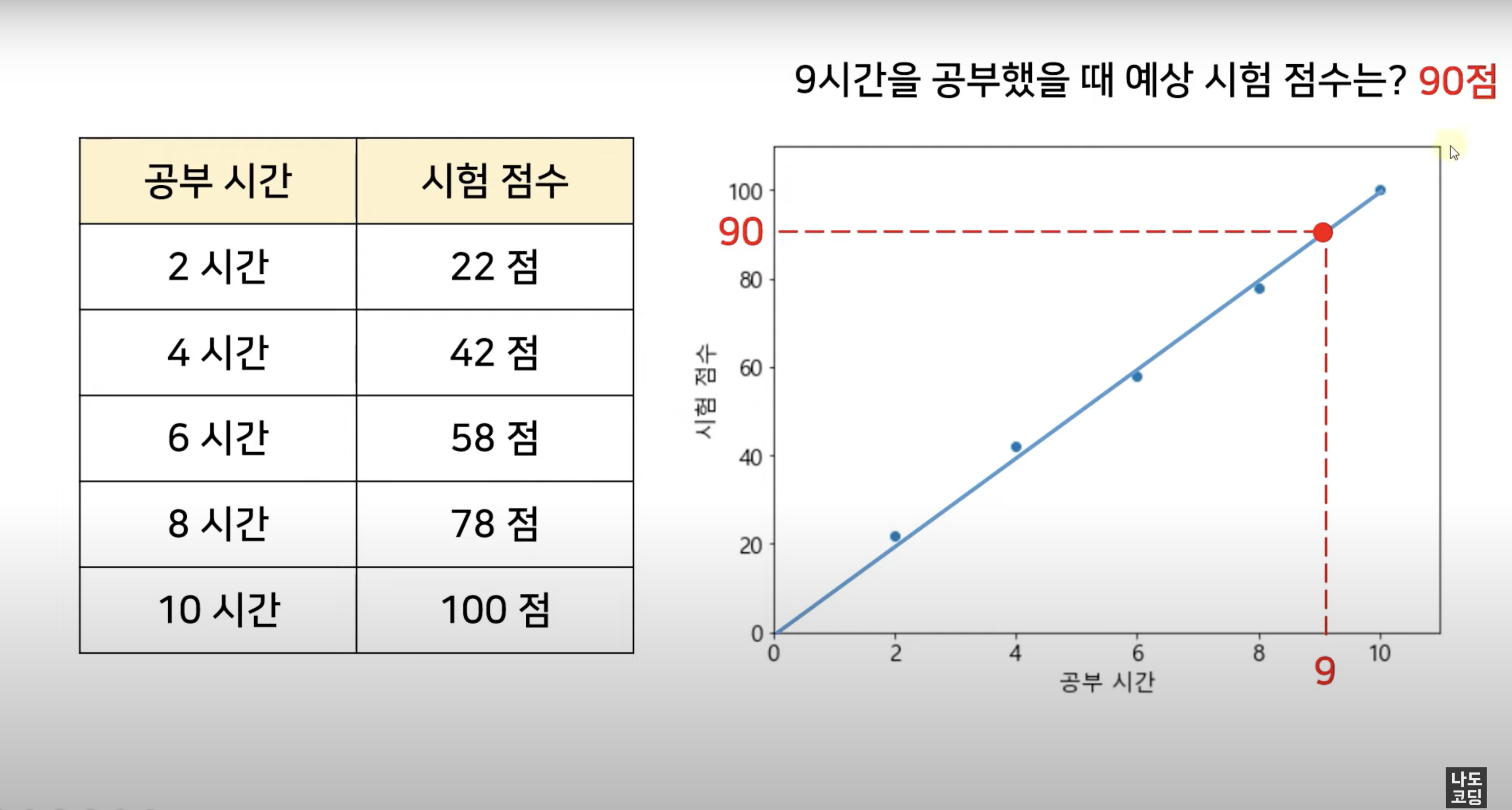
쉽게 말해 변수들 간의 상관관계를 찾는 것, 연속적인 (continuous) 데이터로부터 결과를 예측하는 것이고, 주로 예측 결과가 숫자일 때 적합해요.
예를 들어, 근속연수에 따른 임금, 키에 따른 몸무게, 사용 기간에 따른 스마트폰 가격, ... 등을 알고싶을 때 사용하죠.
Classification 분류
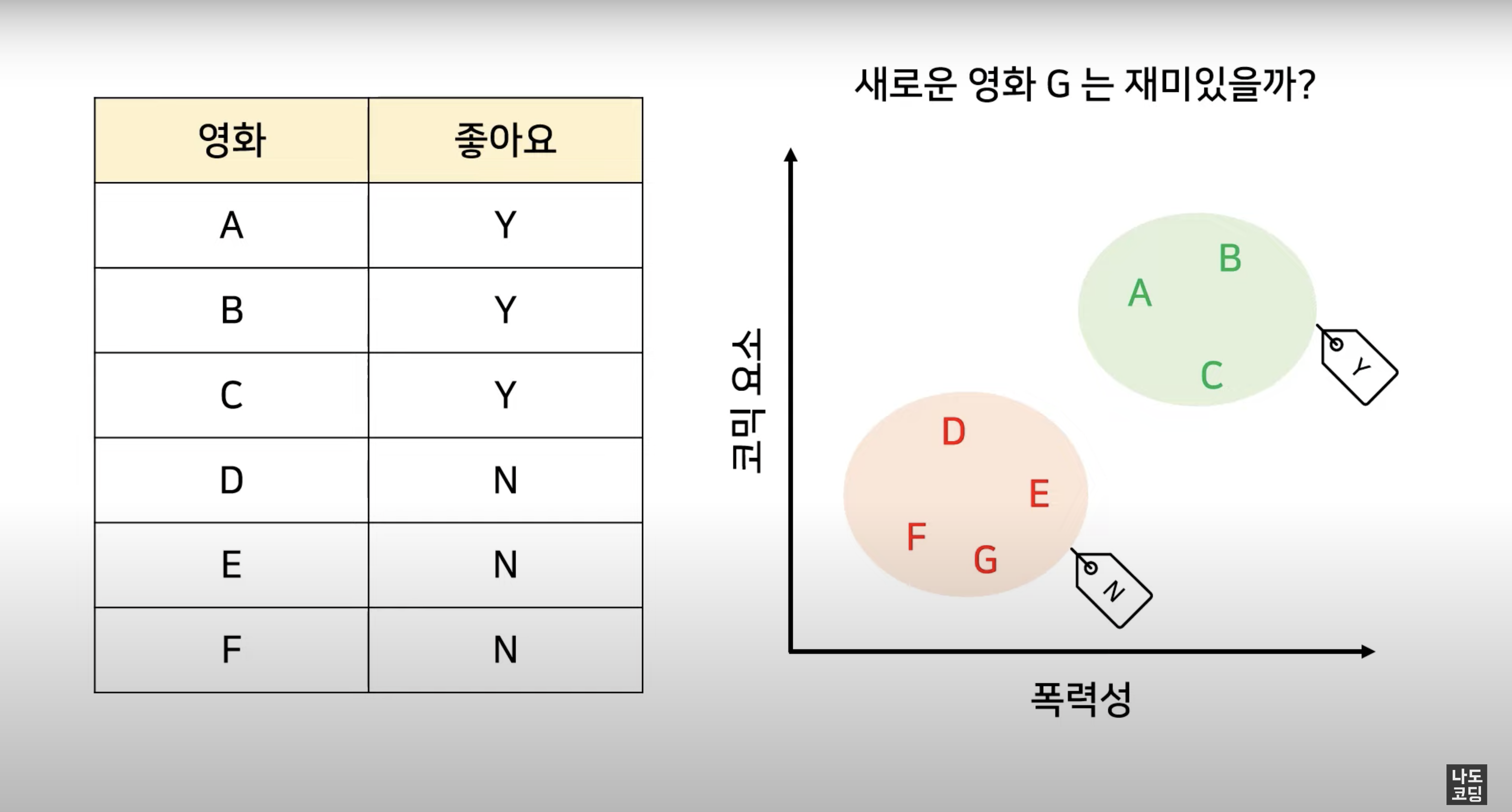
classfication은 주어진 데이터를 정해진 범주 (category) 에 따라 분류하고,
주로 예측 결과가 숫자가 아닐 때 사용해요.
예를 들어, 스팸 메일 필터링, 시험 합격 여부, 재활용 분리수거 품목, 악성 종양 여부, ... 등이 될 수 있겠네요.
Linear Regression 선형 회귀
✅ 용어 체크
X = Independent variable 독립 변수 (원인) = 입력 변수, feature
y = Dependent 종속 변수 (결과) = 출력 변수, target, label
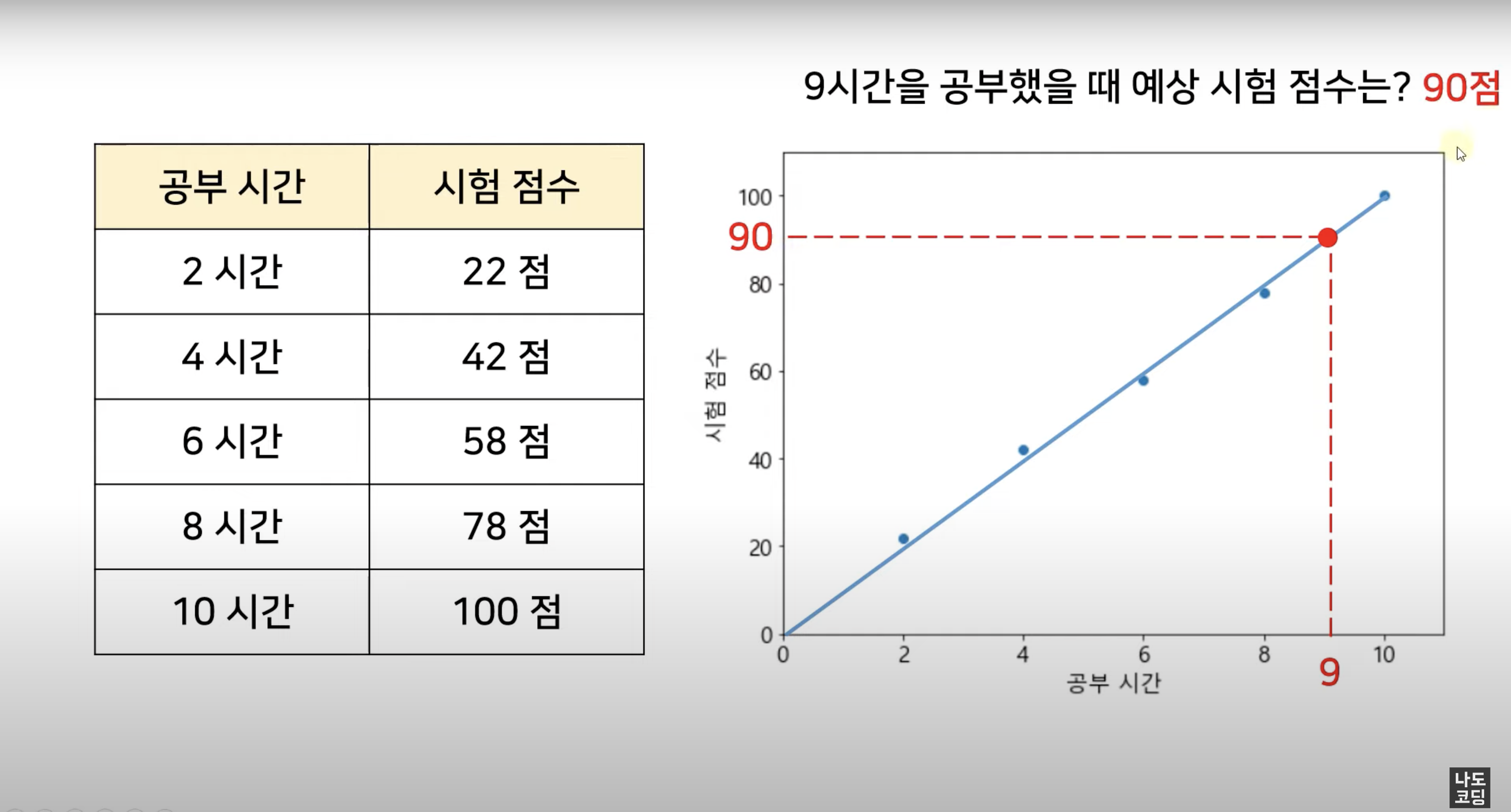
선형 회귀 방법을 통해 우리가 찾으려고 하는 선은
실제 값과 예측 값 차이의 제곱의 합을 최소화한 선이에요.
어떻게 구하냐고요?

실제 값 - 예측 값 = 잔차
이 잔차들을 다 더해서 최소가 되는 직선
➡️ 전체 데이터를 가장 잘 표현하는 최적의 직선, 그 선을 "best-fit" 이라고 해요.
제곱근의 목적은 큰 값의 영향을 줄이고 관계를 보다 선형적으로 만들 수 있고 이는 제곱근 함수가 작은 값보다 큰 값을 더 많이 압축하기 때문이에요.
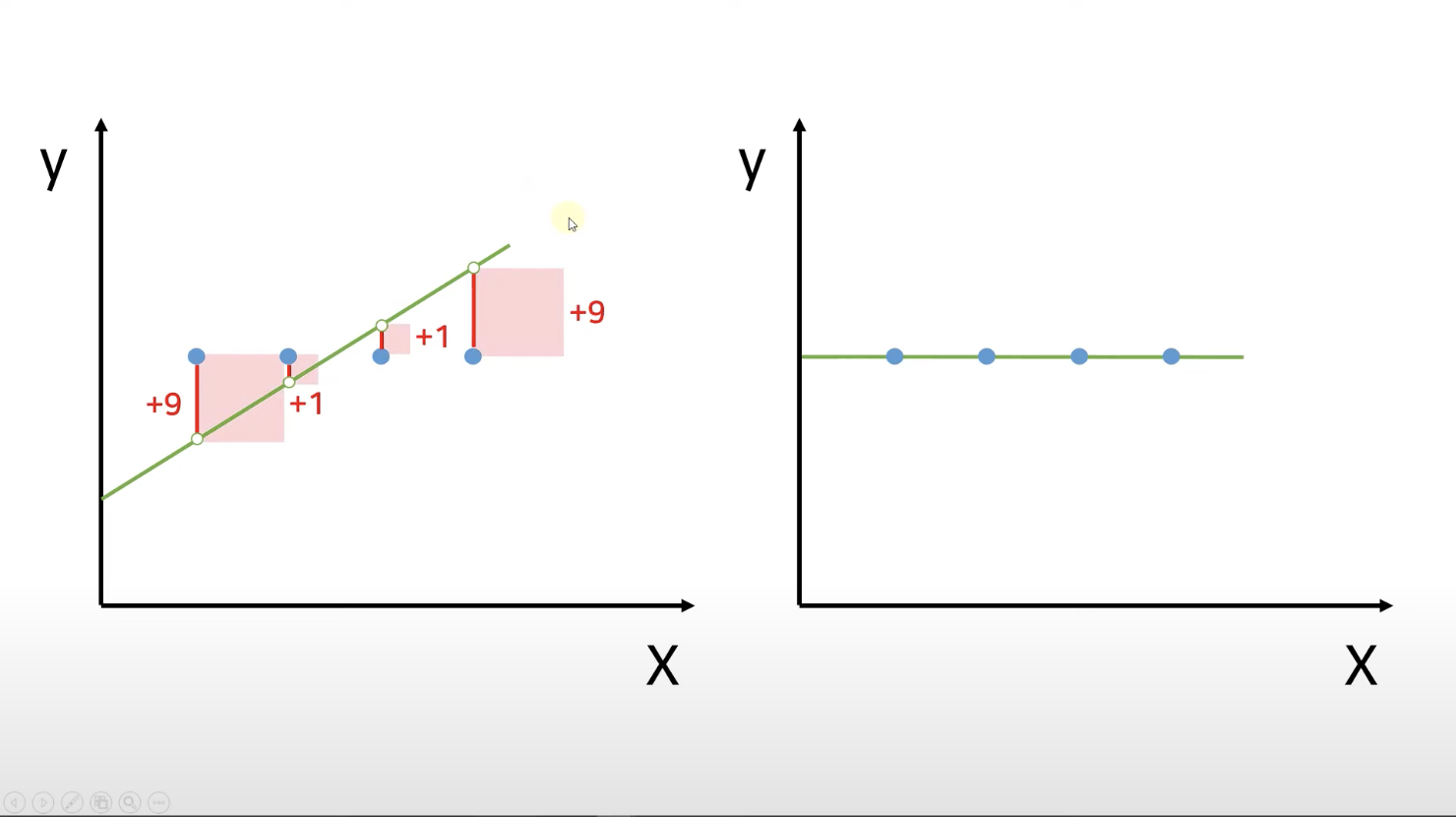
결국 우리가 원하는 것은 최적의 선에 해당하는
y = mx + b
m : 기울기 (slope, coefficient)
b : y 절편 (intercept)
입니다!
Gradient Descent 경사하강법
선형회귀의 단점을 보완하는
- 잔차 제곱의 합 : RSS(Residual Sum of Squares) / SSR
- 최소제곱법 : OLS(Ordinary Least Squares)
👎🏼 노이즈에 취약 (전체적인 패턴에서 벗어난 이상 값을 가진 데이터로 인해 값이 엄청나게 커짐)
👎🏼 독립변수가 하나 이상일 때 최소제곱법을 이용하면 독립변수와 전체 데이터 수에 비례해서 굉장히 높은 비용 발생
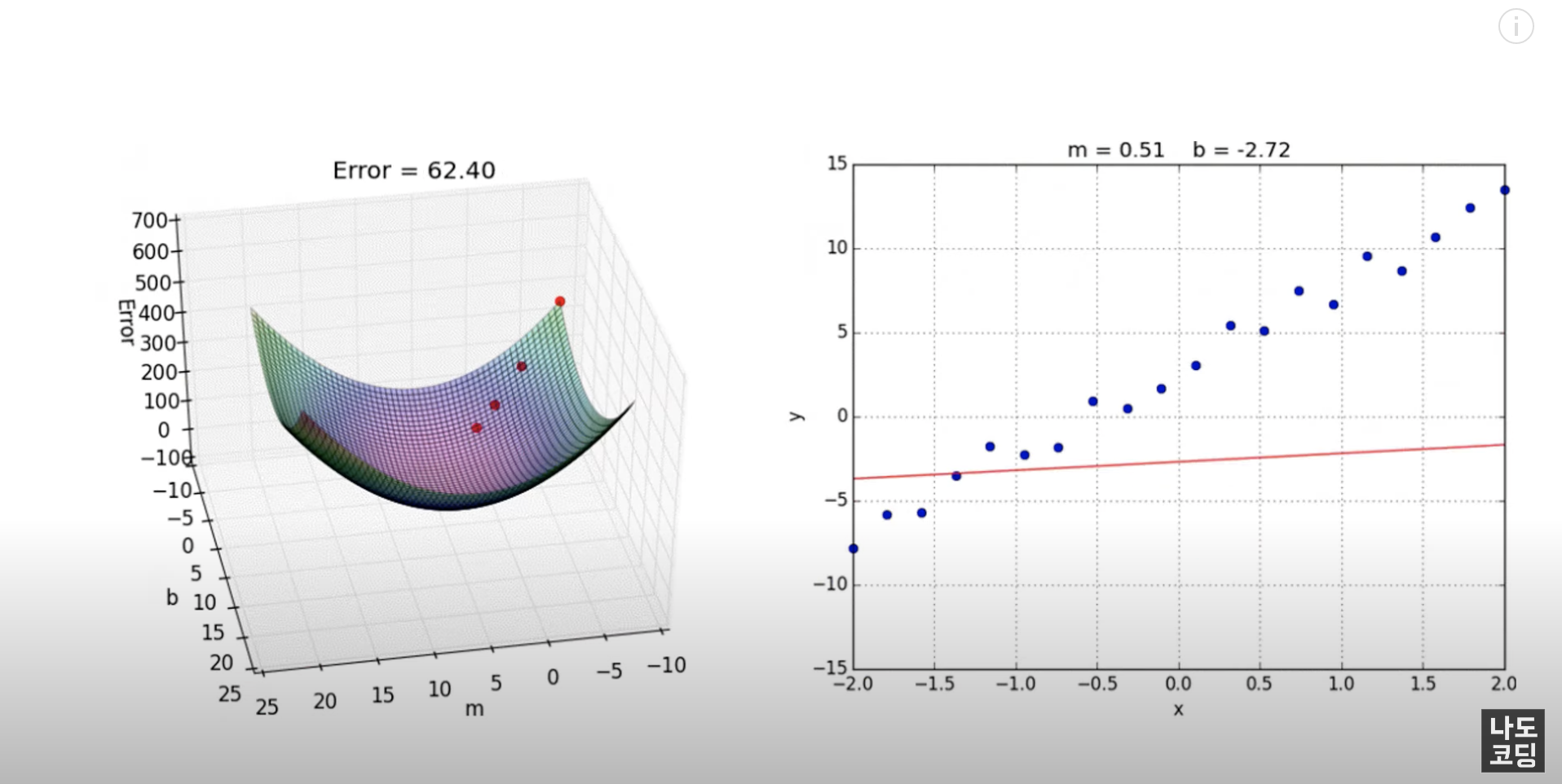
경사 하강법은 선형 회귀에서 비용 함수를 최소화하기 위해 일반적으로 사용되는 최적화 알고리즘입니다. 경사하강법에서 모델의 매개변수(m과 b)는 비용 함수의 가장 가파른 강하 방향으로 반복적으로 조정됩니다. 이는 각 매개변수에 대한 비용 함수의 기울기를 계산한 다음 현재 값에서 기울기의 일부를 빼서 매개변수를 업데이트함으로써 수행됩니다.
무슨 말인지 모르겠죠?
쉽게 말해, 경사하강법은 랜덤으로 지점을 선택, 그 때의 기울기를 확인, 기울기가 낮아지는 쪽으로 m값이 0으로 오게 점점 내려오게 합니다. 결과적으로 기울기가 0이 되는 지점 즉, loss가 가장 낮은 곳으로 오는 것이 목표이죠.
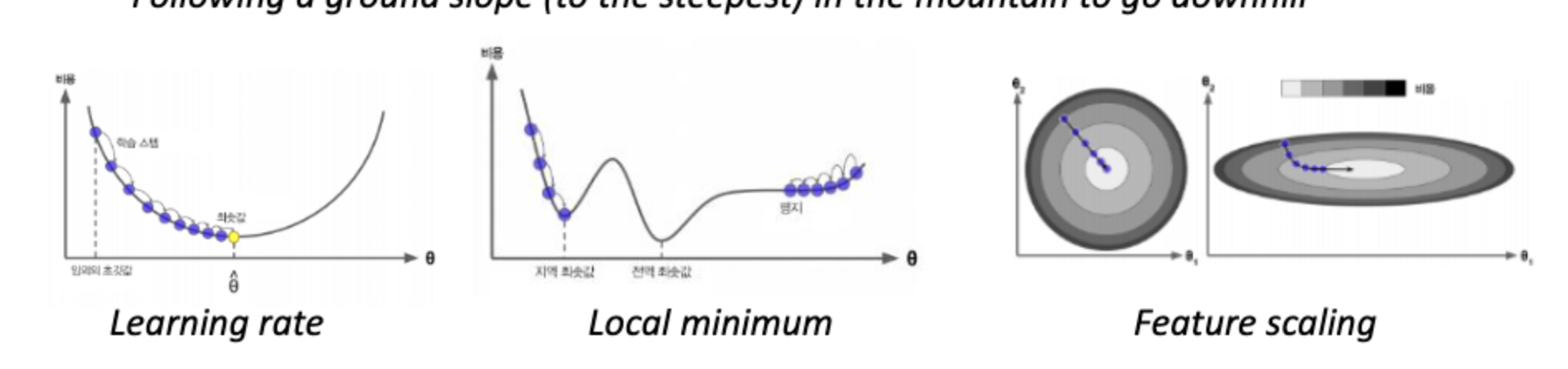
경사 방향으로 계속 따라가기만 하면 시간이 걸려서 그렇지 항상 최솟값을 찾을 수 있습니다. 얼마나 빨리 찾아가는냐는 learning rate에 따라 다르죠.(gradient의 값을 조금씩 반영)
어느 방향으로 가야할지는 안다고 치고 거기의 정도를 찾아야 해요: learning rate 학습률
🆖 여기서 나타나는 문제
1. cost function이 모노토닉 하면 쉽게 찾을 수 있지만 복잡하면 거기에 plateall을 만나게 되면 더 이상 못감 정지
-> learning rate를 조금 더 크게 해서 거기를 지나갔다 하더라도 계속 마주침
2. local minimum에 빠져서 더이상 헤어나오지 못함
🟣 해결 방안은?
1. 데이터를 ramdom하게 choose - shape 다양하게 나타남
2. 시작하는 포인트를 여러 곳에서 해보기 앙상블
Batch Gradient Descent
배치 경사하강법은 전체 데이터 세트가 기울기를 계산하고 각 반복에서 매개변수를 업데이트하는 데 사용되는 일종의 경사하강법입니다. 이는 대규모 데이터 세트의 경우 계산 비용이 많이 들 수 있지만 다른 방법보다 적은 반복으로 최적의 솔루션으로 수렴할 수 있습니다. ( batch / fullset 만 이용 )
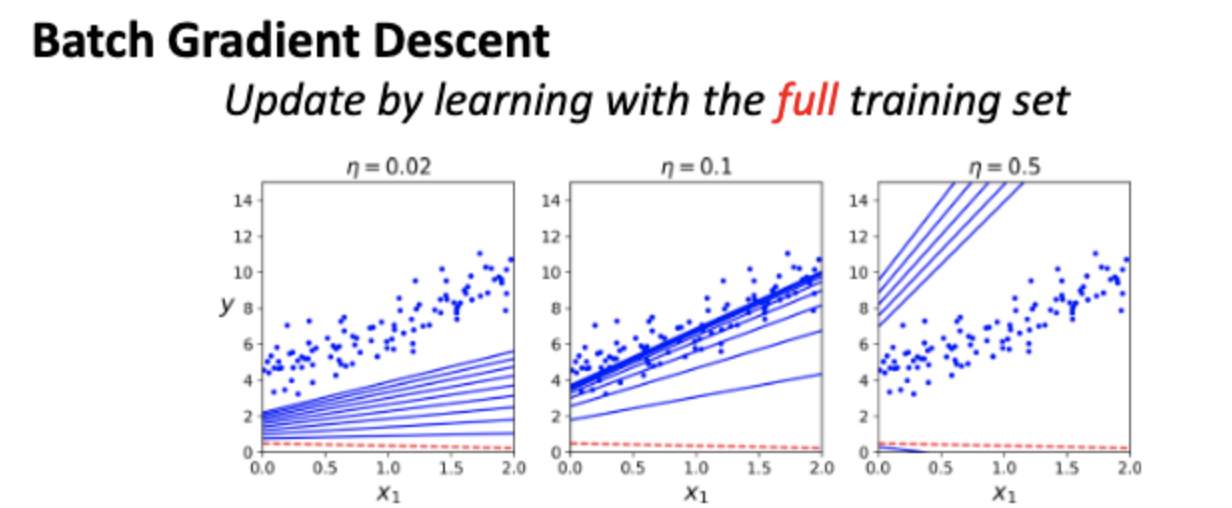
장점
1. 메모리 절약
2. 시간 절약
Stochastic Gradient Descent 확률적 경사하강법
Stochastic Gradient Descent(SGD)는 모델 매개변수가 데이터 세트의 각 교육 예제에 대해 업데이트되는 Gradient Descent의 변형입니다. 이렇게 하면 배치 경사 하강법보다 수렴 속도가 빨라질 수 있지만 노이즈가 발생하기 쉽고 수렴하는 데 더 많은 반복이 필요할 수 있습니다.
즉, 매 단계마다 하나의 데이터를 무작위 선택하고,
그 데이터에 대해서만 기울기 계산해요.
mini-batch gradient descent
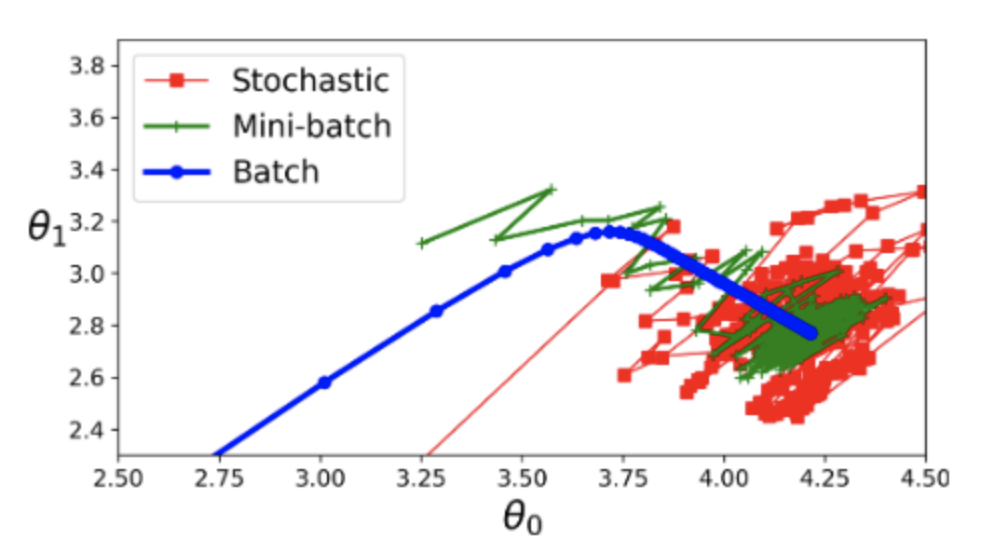
미니 배치 경사하강법은 배치 경사하강법과 확률적 경사하강법 사이의 절충안입니다. 미니 배치 경사하강법에서 데이터 세트는 샘플의 작은 배치로 분할되고 각 배치에 대해 경사가 계산되고 매개변수가 업데이트됩니다. 이는 일괄 처리의 노이즈 감소와 확률적 처리의 수렴 속도의 균형을 맞추기 때문에 배치 경사하강법보다 효율적이고 확률적 경사하강법보다 안정적일 수 있습니다.
2. Polynomial Regression 다차회귀 다항선형회기
y = a0 + a1x + a2x^2 + ...+ anx^n
구하려고 하는 것 : a0, a1, an...
다항 회귀는 직선 대신 데이터에 다항 함수(입력 변수의 서로 다른 거듭제곱의 항을 포함하는 함수)를 맞추는 일종의 회귀입니다. 이는 입력 변수와 출력 변수 간의 관계가 선형이 아닐 때 유용할 수 있습니다.
예를 들어 키를 기준으로 사람의 체중을 예측하려는 경우 직선이 가장 적합하지 않을 수 있습니다. 대신 2차 또는 3차 함수와 같은 다항식 함수가 키와 몸무게 사이의 관계를 더 잘 포착할 수 있습니다.
3. Logistic Regression
로지스틱 회귀는 이진 결과(예 또는 아니오, 참 또는 거짓)를 예측하는 데 사용되는 일종의 회귀입니다. 연속 값을 예측하는 대신 특정 이벤트가 발생하거나 발생하지 않을 확률을 예측하려고 합니다.
예를 들어, 고객의 나이와 소득에 따라 제품을 구매할지 여부를 예측하려는 경우 로지스틱 회귀를 사용하여 고객이 구매할 확률을 추정할 수 있습니다. 로지스틱 회귀는 분류 문제에서 자주 사용되며, 여기에서 데이터 요소를 기능에 따라 다른 범주에 할당하려고 합니다.
wegiht 를 찾아야 하는데 즉, 특정 class에 속할 확률을 찾아내는 것이죠.
Softmax Regression (or Multinominal Logistic Regression)
소프트맥스 회귀(또는 다항 로지스틱 회귀)는 상호 배타적인 여러 클래스의 확률을 예측하는 데 사용되는 일종의 로지스틱 회귀입니다. 가능한 각 클래스에 속하는 이미지의 확률을 예측하려는 이미지 분류 문제에서 자주 사용됩니다.
특정 class만 있는 것이 아닌 여러 개의 class가 있을 경우
(X, y) - y(0, 1, ....) 0의 확률부터 9 다 합하면 1
Support Vector Machine (SVM)
분류 및 회귀 작업 모두에 사용할 수 있는 일종의 기계 학습 알고리즘입니다. SVM의 목표는 데이터 포인트를 서로 다른 클래스로 가장 잘 분리하거나 연속 값을 예측하는 초평면을 찾는 것입니다.
한계: well suited for classfication of complex small or medium sized datasets.
Linear Support Vecrtor Machine
결정 경계가 입력 기능의 선형 함수인 SVM 유형입니다. 클래스를 직선으로 구분할 수 있을 때 일반적으로 사용됩니다.
Nonlinear Support Vector Machine: 결정 경계가 입력 기능의 비선형 함수인 SVM 유형입니다. 이는 더 많은 (비선형) 기능을 추가하거나 커널 기능을 사용하여 달성할 수 있습니다.
Linear SVM Classification
Support Vecor : SVM의 결정 경계(또는 초평면)에 가장 가까운 데이터 포인트입니다. SVM에서 목표는 서로 다른 데이터 클래스를 가장 잘 구분하는 초평면을 찾는 것입니다. 서포트 벡터는 결정 경계에 가장 가까운 데이터 포인트이므로 초평면의 위치와 방향에 가장 큰 영향을 미칩니다.
Hard Margin Classification : 오류 없이 데이터 포인트를 엄격하게 분리하기 위해 결정 경계가 필요한 SVM 유형입니다. 이는 데이터가 선형적으로 분리되지 않을 때 어려울 수 있습니다.
Soft Margin Classification : 결정 경계에 약간의 오류(슬랙 변수라고도 함)가 허용되는 SVM 유형입니다. 이것은 데이터가 선형적으로 분리되지 않거나 데이터에 약간의 노이즈가 있는 경우에 유용할 수 있습니다.
Nonlinear SVM Classification
adding more (non-linear) features to seperate the classes -> Kernelized SVM : 사용하여 원래 입력 기능을 고차원 공간으로 변환하는 일종의 SVM입니다. 이를 통해 변환된 기능 공간에서 비선형 결정 경계를 찾을 수 있습니다.
Polynomial Kernel : 입력 기능 간의 다항식 관계를 캡처하기 위해 SVM과 함께 사용할 수 있는 일종의 커널 함수입니다.
Similarity Featrues : 원래 기능을 유사성 공간으로 변환하는 데 사용할 수 있는 기능 엔지니어링 기술의 한 유형입니다. 여기서 데이터 포인트 간의 유사성은 일부 유사성 메트릭을 기반으로 합니다.
Gaussian RBF Kernel :SVM과 함께 사용하여 입력 기능 간의 비선형 관계를 캡처할 수 있는 일종의 커널 함수입니다. 일반적으로 이미지 분류 문제에 사용됩니다.
마치며