SAC - Soft Actor-Critic

등장배경

1) On-policy learning의 낮은 sample efficiency 극복

ex) TRPO, PPO, A3C

• 매 gradient step 마다 새로운 sample을 요구함

→ 이에 따른 대안으로 past experience 사용 (하지만 NN와 사용시 안정성과 수렴성 문제가 존재)

2) brittle 하고 hyper-parameter에 영향을 많이 받음

ex) DDPG → 이 논문의 baseline

Contribution

1) continuous 한 state, action space에서 안정적인 알고리즘 제안

2) maximum entropy framework 소개

• exploration 과 robustness(견고함)에 효과적
• 이전 연구들은 maximum entropy를 on-policy 방식에만 적용했음

3) soft Q-learning에 기반한 maximum entropy 가 approximate inference와 연관되어 갖고 있는 complexity와 potential instability 제거

→ 2022.07.07 이 부분은 추가적인 이해 필요!

배경지식

1) actor-critic 방식에서는 policy(actor)와 value function(critic) 이 joint하게 최적화된다.

• 많은 경우 on-policy 방식을 사용하며 entropy를 regularizer로 사용하지만 이 논문은 off-policy와 maximum entropy를 사용한다는 차이가 있다.

2) DDPG의 한계

• off-policy actor-critic 방식의 일종으로 Q-function을 최대화하는 deterministic actor를 사용하고 있지만 deterministic actor network와 Q-function approximate network 사이의 interplay가 수렴을 어렵게 만든다.

→ 이를 보완하기 위해 stochastic actor를 도입하고 entropy maximization 목표도 추가로 설정한다

번외) $\rho_{\pi}(s_t)$ 와 $\rho_{\pi}(s_t,a_t)$ 는 policy에 의해 각 action과 state에 흩어져있을 distribution을 의미하는 state와 action-state marginal

3) Maximum entropy RL

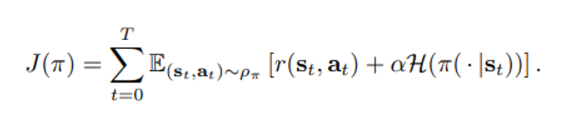
위와 같은 objective를 만족해야 하며 의미는 어떤 policy에 대해 이로인한 state marginal에 대해 일반적인 reward 항과 엔트로피항의 합을 최대화해야 함을 의미한다.

$\alpha$는 policy가 얼마만큼의 stochasticity를 가져야 최대가 되는지 결정하는 상수

• 기대효과는 더욱 활발한 탐색
• optimal behavior에 가까운 여러 policy를 대부분 알아낼 수 있다.
• learning speed 개선

4) Soft Q Learning

Soft state value function이 아래와 같이 정의된 이유?

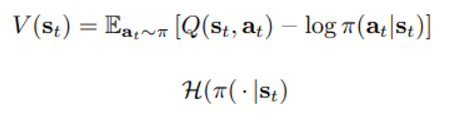
참고) 뒤의 policy에 대한 항은 Expectation을 나오면서 아래의 엔트로피와 같이 변형가능하다.

---

이에 대한 직관적 이해를 위해 다시 식을 다음과 같이 변형시키면

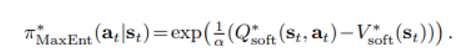
어떤 action을 취할 확률은 state에 대한 평균적인 reward와 마찬가지로 그 state를 취하면서 가장 큰 reward 편차를 기록하는 action의 reward 차의 exp하게 비례하여 할당하면 정당하다는 방식으로 이해할 수 있다.

• lemma 1 : 위와 같이 정의된 state value function V에 대해 아래와 같은 soft-Bellman operator를 적용하면 soft-Q value로 수렴할 것이다.
  
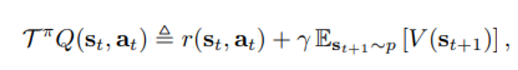
  위의 state-value function V에서 뒷 항을 엔트로피로 바꿔 밖으로 빼낸 후 reward를 다시 아래와 같은 꼴로 변형하면
  
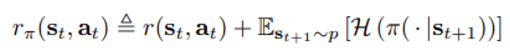
  원래 policy evalution 에서 수렴성 증명 방식과 같은 방식으로 증명가능하다.

---

편리성을 위해 정의된 policy 공간 $\Pi$ 안의 리스트 중 현재 Q-function 의 exp과 KL distance가 가장 작은 policy를 다음 policy로 설정한다.

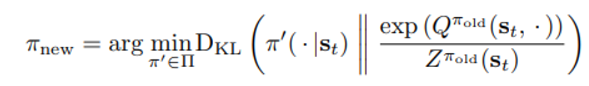
수식에서 z는 normalization term이며 gradient에는 영향을 주지 않는다.

• lemma 2: 위와 같은 방식으로 선택한 new policy에 대해 항상 $Q^{\pi_{new}}(s_t,a_t) \geq Q^{\pi_{old}}(s_t,a_t)$ 가 성립한다.

이 부분을 항상 까먹음

policy paratmer $\phi$는 아래와 같은 objective를 minimize 하면서 얻어지기 때문에

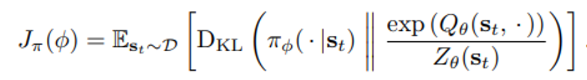
다음과 같은 두 줄의 식이 성립하는 것이다.

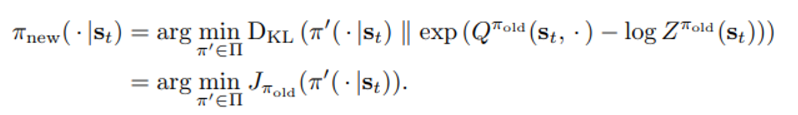
이는

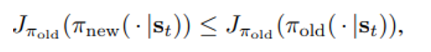
과 동치이며 J는 KL divergence의 정의에 의해 아래와 같은 관계로 표현가능하다.

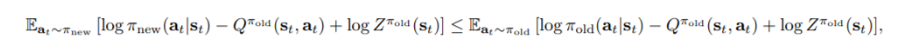
Z는 앞서 말한 것과 같이 단순히 normalization term이므로 제거하면 아래와 같은 inequality를 얻는다.

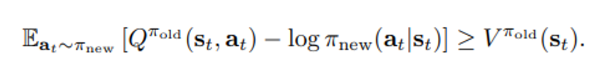
Soft Bellman equation에 위의 inequality와 $Q_{old}$의 정의를 재귀적으로 적용하면 최종적으로 아래와 같은 식을 통해 증명하고자 했던 바를 얻는다.

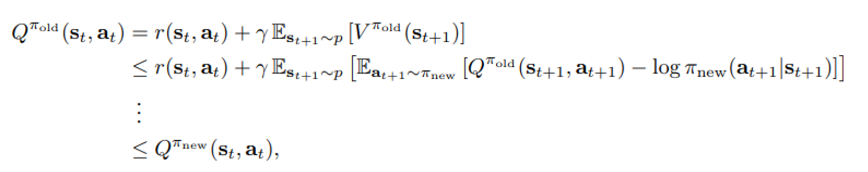
위에 제시한 방법은 모두 tabular case 에 대한 내용으로 continuous domain에 적용을 위해서는 Q 값에 대한 function approximator가 필요하다.

또한 policy evaluation과 policy improvement 를 two step으로 돌리기에는 계산적인 무리가 있으므로 이번 논문의 SAC 알고리즘을 소개한다.

본문내용

1) function approximation

state value function $V_{\psi}(s_t)$, soft Q-function $Q_{\theta}(s_t,a_t)$, policy $\pi_{\phi}(a_t|s_t)$ 로 표현한다.

배경지식에서 소개한 것과 같이 policy evaluation과 improvement를 수렴까지 돌리는 것 대신 SGD를 통해 Q-function과 policy 가 모두 optimize 되도록 alternate 한다.

ex) value function 같은 경우에는 output을 그대로, policy는 Gaussian policy의 mean과 covariance 를 NN을 통해 얻어 사용하도록 한다.

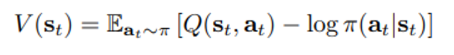
State value function은 위와 같이 정의되었기 때문에 원래 대로라면 별도의 parameter가 필요하지 않지만

• stabilize training
• other network와의 simultaneous 한 training 가능성

과 같은 이점들이 있어 별도의 NN을 사용하고 있다.

---

각 함수의 objective function과 parameter update 방식은 아래와 같다.

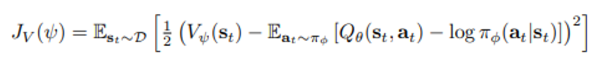
위의 식은 soft state-value function의 정의인 아래와 같은 식을 따라

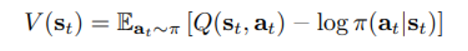
제곱 합이 최소가 되는 방향으로 업데이트 되며 gradient는 아래와 같다.

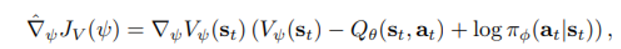
주의) 이 때 sample하는 action은 replay buffer가 아닌 현재 policy 로부터 기인한 것이다.

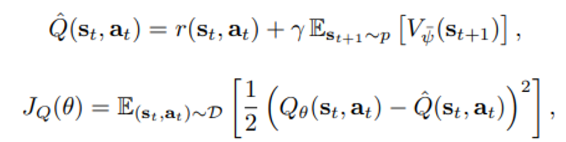
이 때 V의 parameter notation은

• exponentially moving average
• match current value function weights periodically

하는 방식으로 선정된다.

gradient은 아래와 같다.

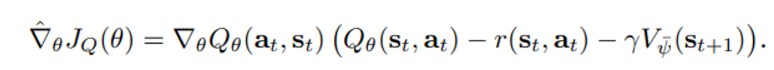
앞서 언급한 policy 선정 방식으로부터 우리는 policy에 대해 아래와 같은 objective를 정한다.

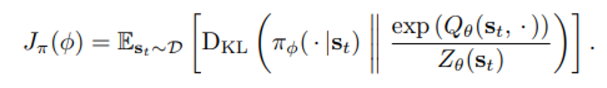
위의 식에서 Expectation 내부에 있는 식은 다시 E_{\pi}[log\pi_{\phi}-Q_\theta(s_t,.)] $ 꼴로 표현되는데 policy에 대해 아래와 같이 action을 reparameterize 하는 전략을 사용해 최종적인 objective function은 다음과 같이 표현된다. 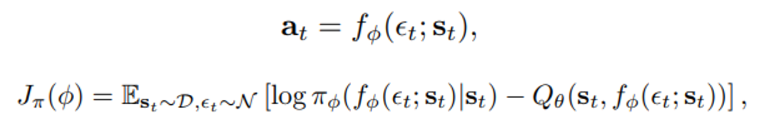 아래의 objective function 식을 통해 randomness 는 action 이 아닌 $\epsilon_t에 있음을 알 수 있다.

Reparameterize 전략을 사용하는 이유는 아래의 사이트를 통해 참조하면 좋다.

초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (3)

policy에 대한 gradient은 다음과 같은 식으로 정리되는데

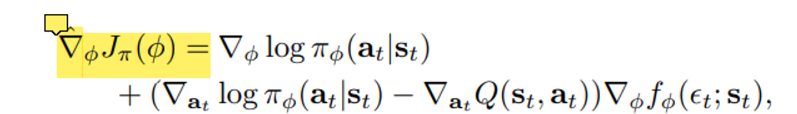
이는 아래의 사이트에 제시된 유도 과정을 참고하면 좋을 것이다.

Gradients of the policy loss in Soft-Actor Critic (SAC)

---

전체적인 알고리즘은 아래와 같다.

여기서 주의할 점은

• policy improvement step에서 발생 가능한 positive bias를 제거하기 위해 두 개의 Q-function을 사용해 이 중 작은 값을 실제 Q function으로 설정
• state value function V의 parameter를 업데이트 하고 target을 만들 때 내분 형식으로 서서히 새로운 parameter를 참고하는 방식으로 업데이트한다. (exponentially moving average 방식

---

SAC 성능에 영향을 미치는 요소들

• policy 의 성질 → Stochastic , Deterministic

  이번 논문에서 엔트로피는 value function과 policy 의 objective function에 등장하는데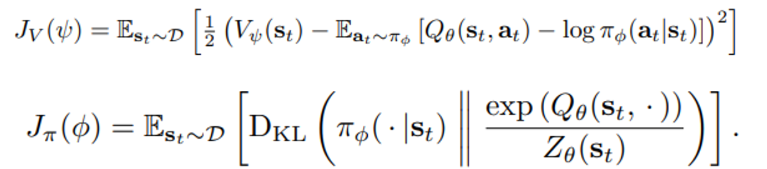

  
  (위의 두 식에서 Expectation 안에 들어간 $log\pi$ 항이 Entropy를 의미함)

policy에서는 premature converge를 제한, value function에서는 exploration을 증가시키는 효과가 있다.

이러한 효과를 비교하기 위해 앞서 reparameterization 전략에서 exploration noise를 고정시켜버려 deterministic 한 상황을 연출한 후 가장 어려운 task 에 대해 성능을 비교한 결과는 아래와 같다.

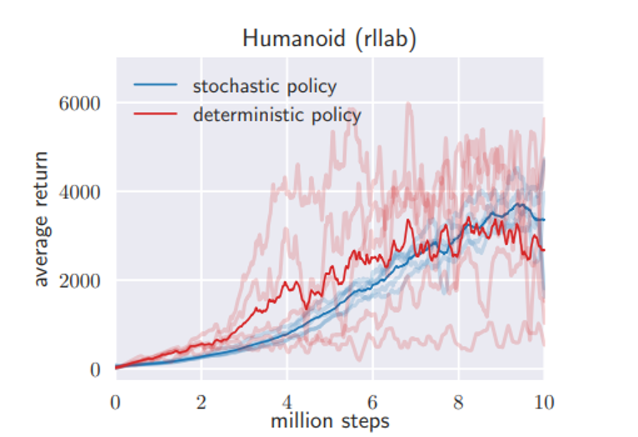
빨간색 그래프는 확실히 stability가 저하된 모습을 확인할 수 있다.

• Best performance를 내기 시작하는 후반부에는 deterministic policy(탐색을 줄이기 위해)를 도입하는 것이 성능을 높일 수 있다.
• Reward 의 scale이 올라가게 되면 엔트로피의 영향이 낮아지기 때문에 낮은 exploration 효과를 보이며(deterministic한 행동양상) 반대로 scale이 너무 작다면 엔트로피가 극대에 가까워져 모든 policy를 uniform 하게 만들어 학습하지 못하는 현상을 겪는다.
• Value function을 업데이트하는 exponentially moving average 방식은 너무 빠르게 변할 경우 instability를 증가 시키지만 또 너무 느릴 경우 학습이 느려진다는 단점이 존재하므로 적당한 온도를 찾아야 할 것이다.