😃[5주차 - Day5]😃

확률분포

[이산확률분포]

밀도추정

풀려고 하는 가장 큰 문제는 밀도추정이라고 할 수 있습니다. N개의 관찰데이터 x1, ... , xn가 주어졌을 때 분포함수 p(x)를 찾는 것. 확률분포를 완벽하게 구할 수 있다면 모든 문제를 다 풀 수 있습니다. 가장 어떻게 보면 제너럴한 문제입니다.

이를 구하는 일반적인 방법론으로는 다음과 같습니다.

확률의 density를 구하고자 할 때, p(x)를 파라미터화된 분포로 가정합니다. 회귀문제에서는 주로 p(t|x), 분류문제에서는 p(C|x)를 찾기를 원합니다.

이 분포의 파라미터를 찾으려면 빈도주의 방법과 베이지언 방법이 있습니다. 빈도주의 방법은 likelihood를 최적화시키는 과정을 통해 파라미터 값을 정합니다.

베이지언 방법은 파라미터의 사전확률을 가정하고 베이즈 룰에 따라 파라미터의 사후확률을 구하는 방법입니다. 이를 사용해 파라미터를 찾았다면, t나 C를 예측을 할 수 있습니다.

켤레사전분포는 사전확률의 함수형태가 사후확률과 같아지도록 해주는 것입니다.

이항변수(Binary Variables) - 빈도주의 방법

x가 0 아니면 1 둘중 하나의 값을 가진다고 가정하도록 하겠습니다.

단순한 확률이지만 이를 파라미터를 통해서 나타낼 수 있습니다.
단 두가지 확률이 있을 때, 1이 나올 확률을 파라미터화 시켜서 뮤라고 하고, 0이 나올 확률은 1-뮤의 값을 가집니다.

임의의 x값이 주어졌을 때, 베르누이 분포로 표현하자면 뮤의 x승, 1-뮤의 1-x승을 곱한 값으로 표현할 수 있습니다.

이는 불확실성을 잘 표현하지 못하고, 과적합된 결과를 낳을 수 있습니다.

이항변수 - 베이지언 방법

위와 같은 오류를 위해 베이지언 방법을 사용할 수 있습니다.

조금 다른 방법으로 표현하자면, 사건을 N번을 했을 때 전체 결과에 대해 x가 1인 경우를 m번 관찰할 확률을 정의합니다.

m은 0부터 N까지의 값을 가질 수 있습니다. 이는 이항분포인데요.

앞에서 봤던 베르누이 분포와 이항분포는 데이터를 보는 다른 두가지 관점이라고 할 수 있습니다.

베르누이 시행은 각각을 반복한다고 할 수 있습니다. 이것들은 각각 확률변수입니다. 여러개의 확률변수입니다.

x가 1인 경우를 몇 번 관찰했는가에 대한 이야기가 이항분포입니다. 이는 하나의 확률 변수를 가지게 됩니다.

베이지안 방법을 사용하기 위해서는 파라미터들의 사전확률을 정해야합니다. 사후확률과 사전확률이 동일한 함수형태를 가지게 하는 것이 중요합니다.

베타분포를 사용하여 베이지언 방법으로 문제를 해결하는데 이때 베타분포를 켤레사전분포로 사용합니다.

베타분포는 뮤에 대한 분포입니다. 원래는 파라미터로 주어진 뮤가 이제는 뮤에 대한 분포를 구하게 됩니다. 이 뮤는 또 다른 파라미터 a,b에 의해서 정의됩니다.

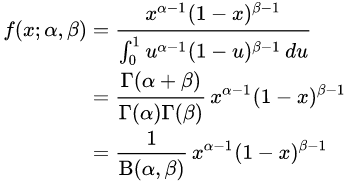
여기서 감마함수라는 것이 사용되는데, 감마함수는 계승(factorial)을 실수로 확장시키는 함수입니다.

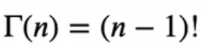
이 감마함수가

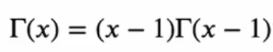
위 성질을 만족하기 때문에 (n-1)! 의 성질을 만족하는 것입니다.

---

여기서 베타분포에서 a값이 커질수록 뮤의 값이 0.5보다 큰쪽에서 형성이 되고, 반대의 경우도 마찬가지 입니다. 또한 a값 b값이 모두 1이라면 직선의 형태로 베타분포가 나타나게 됩니다.

또한 b와의 차이가 크면 클수록 오른쪽으로 샤프하게 나타나게 됩니다.

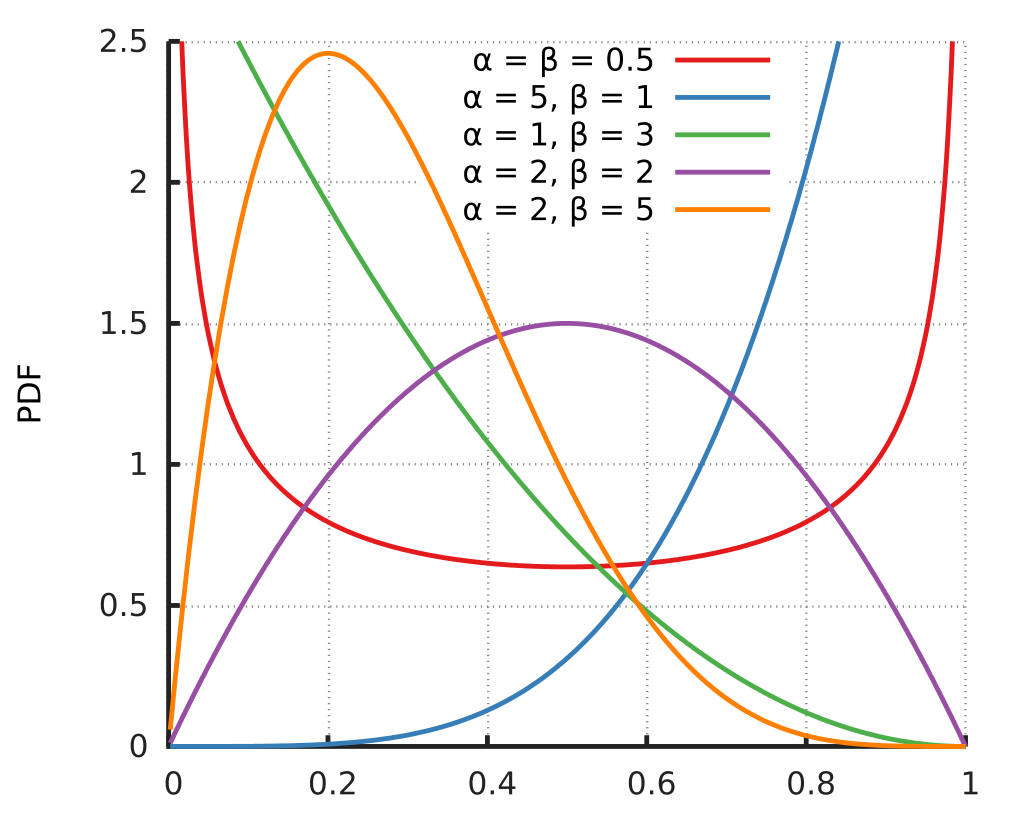
또한 베타분포는 normalized임이 증명되어 있습니다.
(전체를 적분했을 때 그 값이 1이 됩니다 == normalized)

베타분포의 기댓값 및 분산은 https://m.blog.naver.com/mykepzzang/220843077734 에 증명이 되어 있습니다.

다항변수에 대한 기댓값 및 likelihood 를 찾을 수 있고, 이에 대한 추정, estimate도 할 수 있습니다.

다항분포 또한 구할 수 있고, 모든 mk를 합했을 때 N이 됩니다.

이를 위한 켤레사전분포는 디리클레 분포를 사용할 수 있습니다. 베타분포를 일반화 시킨 모양입니다.

디리클레 분포는 normalization이 되는데 이에 대한 증명도 찾아볼 수 있습니다. 적분 했을 때 1이 된다는 성질입니다.
이에 대해 일반적인 경우에도 성립합니다. 귀납법으로 증명이 가능합니다.

JUPYTER NOTEBOOK

Uniform Distribution

from scipy.stats import uniform

n = 10000
start = 10
width = 20
data_uniform = uniform.rvs(size=n, loc = start, scale=width)

ax = sns.distplot(data_uniform,
                  bins=100,
                  kde=True,
                  color='skyblue',
                  hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Uniform Distribution ', ylabel='Frequency')

Bernoulli Distribution

from scipy.stats import bernoulli
data_bern = bernoulli.rvs(size=10000,p=0.8) # mu == p
# 빈도를 절반으로 하고 싶으면, p를 0.5으로 세팅하면 됩니다.

np.unique(data_bern, return_counts=True)

ax= sns.distplot(data_bern,
                 kde=False,
                 color="skyblue",
                 hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Bernoulli Distribution', ylabel='Frequency')

Beta Distribution

from scipy.stats import beta
a, b = 0.1, 0.1
data_beta = beta.rvs(a, b, size=10000)

ax= sns.distplot(data_beta,
                 kde=False,
                 color="skyblue",
                 hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Beta Distribution', ylabel='Frequency')

Multinomial Distribution

from scipy.stats import multinomial
data_multinomial = multinomial.rvs(n=1, 
		   p=[0.2, 0.1, 0.3, 0.4], size=10000)

data_multinomial[:50]

for i in range(4):
  print(np.unique(data_multinomial[:,i], return_counts=True))