😃[2주차 - Day3]😃

벡터의 내적 & 투영

두 벡터 u,v 간의 내적이 0이면 두 벡터는 직교 (orthogonal) 입니다.

두 벡터 u, a가 있을 때, 벡터 u를 a 위에 투영한 벡터를 projau라 하고 다음과 같이 구합니다.

proj (ection) a (위에) u (를 떨궜다) 라는 뜻입니다.

투영된(프로젝션) 벡터와 남은 보완(컴플리먼트) 벡터는 90도의 관계를 이룹니다. 이것이 무슨 뜻이냐면, 벡터를 a에 투영하고 나면 a에 떨구고 남은 u벡터의 방향성이 b벡터라고 하겠습니다. 그렇다면 b벡터는 보완 벡터라고 부르게 되고, 이는 u - projau 로 표현할 수 있습니다.

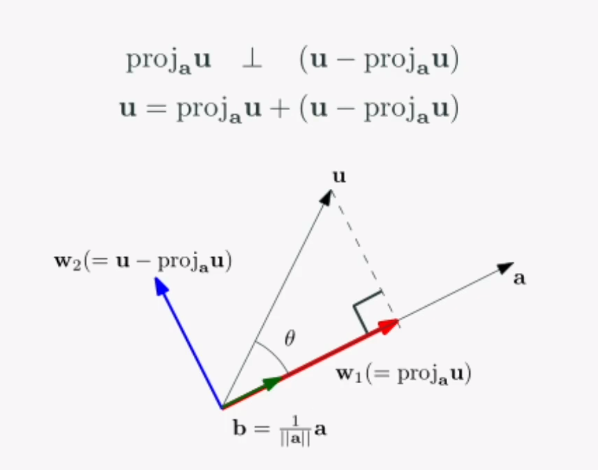
고로, 프로젝션된 벡터와 컴플리먼트 벡터는 직교한다. 그리고 프로젝션 벡터와 컴플리먼트 벡터를 합하면 원래의 벡터로 돌아올 수 있다는 것. 프로젝션을 하면 직교분할을 얻을 수 있다는 것을 얻을 수 있습니다.

직교행렬 (orthogonal martix)

주어진 행렬의 모든 열벡터가 서로 직교한다면, 이를 직교행렬이라고 합니다. 예시로,

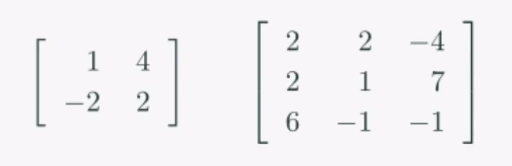
이런 행렬들이 직교행렬이라 할 수 있는데, 서로 내적해보면 그 합이 전부 0이 되는것을 알 수 있습니다.

(1×4 + -2×2) = 0 , (2×2 + 2×1 + 6×-1) = 0 등등

정규직교행렬 (orthonormal matrix)

이 중에서도 특별한 녀석이 있는데, 정규직교행렬이라고 하는 것이 있습니다. 이는 직교행렬이면서 모든 열벡터의 크기가 1인 행렬입니다.

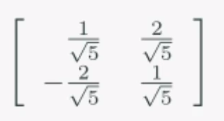
직교행렬을 이용한 선형시스템

선형시스템 Ax=b에서 행렬 A가 직교행렬이면, 해 x는 역행렬의 계산없이 다음과 같이 구할 수 있습니다.

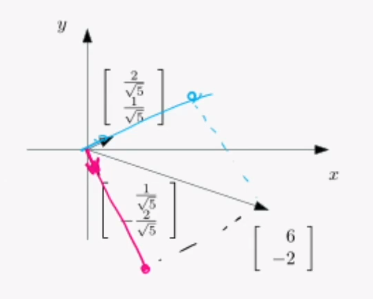
축 별로 따로 계산할 수가 있습니다. 이건 굉장히 편한 방법인데, b에서 수선의 발을 내려 스칼라 값만큼 곱한 a만큼 이동하면 그것이 바로 Ax=b의 해라는 말입니다.

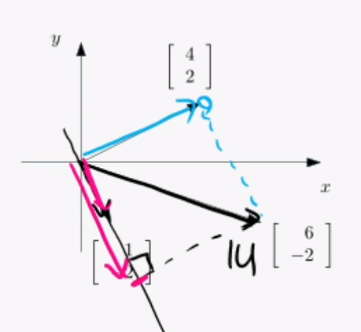
이 그림과 같은 예시로, 분홍색은 수선의 발을 내린만큼, 파란색또한 수선의 발을 내린만큼 이동하면 병렬으로 구할 수 있다는 것입니다.

하지만 이는 직교행렬이어야만 가능합니다.

정규직교행렬이라면?

정규직교행렬에서는 분모가 무조건 1이 되기 때문에, 내적만 곱하면 답이 됩니다.

QR 분해

QR 분해는 Q : 정규직교행렬, R : 상삼각행렬(upper trianglar matrix)로 이루어진 행렬분해입니다.

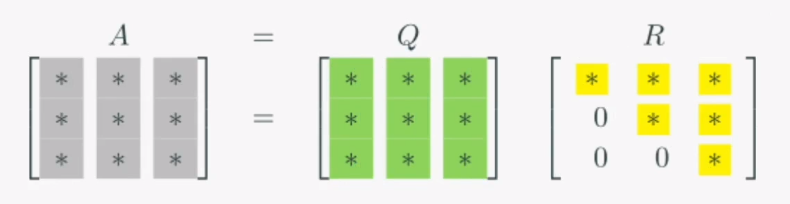
고로, Ax-b 문제를 분해해보면,

(QR)x = b

Q(Rx) = b

Qy = b

로 보았을때,

내적으로 정규직교행렬의 해를 구하고, 후방대치법을 사용하여 Rx = y의 해를 구하면 됩니다.

QR분해는 그람-슈미트 과정을 행렬로 코드화 한 것입니다. QR분해는 주어진 행렬에서 정규직교성을 추출하여 계산의 편의를 도모한다는 점이 핵심입니다.

QR 분해 vs LU 분해

LU 분해의 경우, 선형시스템을 풀 때 병렬처리 할 수 없습니다.

QR 분해의 경우, Q 행렬이 꽉찬 구조를 가진 행렬이기 때문에 메모리 사용량이 많은 단점이 있습니다.

특이값 분해 (SVD, Singular Value Decomposition)

LU 분해와 QR 분해는 n x n 정방행렬에 대한 행렬분해이고,

SVD, 즉 특이값 분해는 일반적인 m x n 행렬에 관한 행렬분해입니다. 특이값 분해는 직교분할, 확대축소, 차원변환과 관련이 있습니다.

특이값 분해는 주어진 행렬을 세 행렬의 곱으로 나누는 행렬분해입니다.

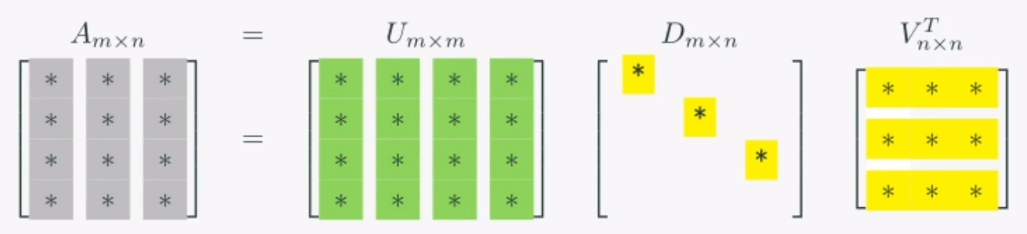
U: 입력 차원인 Rm 공간에서의 회전
D: 입력 차원인 Rn 공간에 대해 축방향으로의 확대축소한 후, Rn -> Rm으로 차원 변환
V: 입력 차원인 Rn 공간에서의 회전

위와 같은 세 과정을 말합니다.

주성분분석

공분산 행렬에 관한 어떤 직교분해를 한다!

2차원 평면을 1차원 직선으로 변환할 수 있는 방법입니다. 펼쳐져 있는 데이터를 한 직선에 수선의 발을 내려 데이터를 응집시킵니다. 이렇게 하면 scatter된 데이터가 하나의 직선으로 모일 수 있고 응집성이 강한 방향으로 해당 데이터들의 경향을 파악할 수 있습니다.

공분산행렬에 대해 주성분분석(PCA)은 다음과 같습니다.

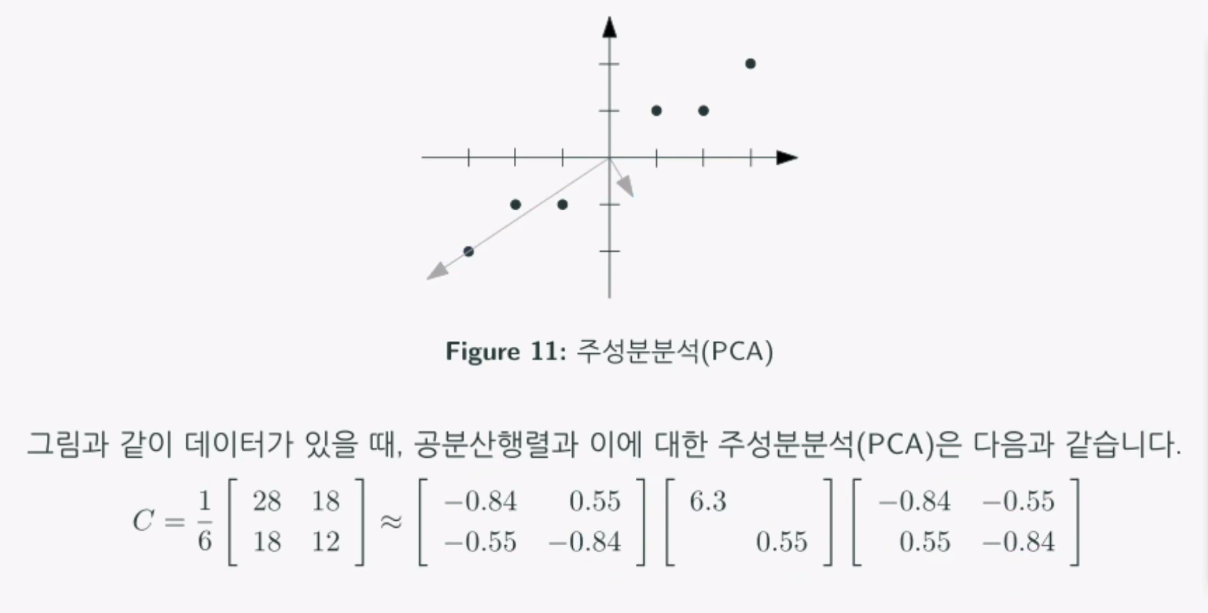
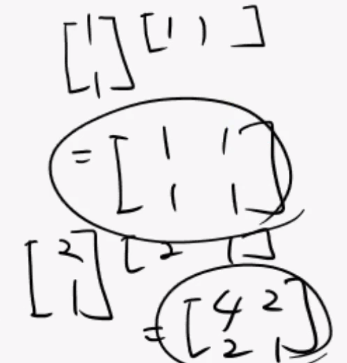
이런 내적의 과정을 거쳐 모든 점을 합하면 데이터는 6개, 공분산행렬은 위와같은 28 18 18 12 의 2 x 2 행렬이 나오게 된다고 합니다.

(사실 잘 모르겠으니 공분산행렬을 조금 더 공부하기)

벡터공간과 최소제곱법

공간

공간은 덧셈연산에 닫혀있고, 스칼라 곱 연산에 닫혀있는 집합입니다. 대표적인 공간은 n-차원 벡터의 집합입니다. 모든 n-벡터 집합은 공간이라고 할 수 있습니다.

최소제곱법

최소제곱법은 선형시스템 Ax=b에 대한 해 x가 없음에도 불구하고, 할 수 있는 최선의 대안 x̅ 를 도출하는 기법입니다. 최소제곱법은 원래의 선형시스템 Ax=b 가 아닌 아래의 선형시스템을 해결합니다.

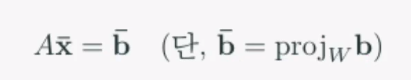
이 방법은 목표 b와 달성가능한 목표의 차이를 나타내는 벡터의 제곱길이를 최소화시키는 의미를 가지기 때문에 최소제곱법 (least squares method)이라고 불리웁니다.

이 해를 구하기 위해서는 주어진 선형시스템의 양변에 전치행렬을 곱하면 구할 수 있습니다.

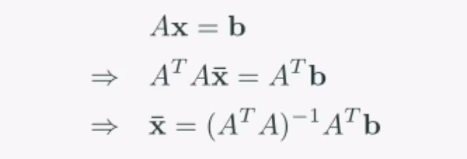
원래의 선형시스템을 만족하는 해는 절대로 구할 수 없지만, 근사해(approximate solutin)을 구할 수 있습니다. b를 평면에 투영한 결과물의 근사해를 찾아낼 수 있는 것입니다.

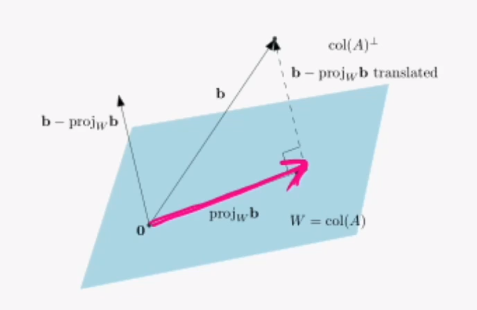
이는 흔히 알고 있는 선형회귀 (linear regression) 에 사용될 수 있습니다.

통계학, 기본개념

Median (중앙값)

평균으로 구했을 때, 극의 값(최대, 최소)에 영향을 많이 받기 때문에 이를 소거하기 위해 중앙값을 사용합니다.

import statistics

a = [79, 54, 74, 62]

statistics.mean(a)   # 평균
statistics.median(a) # 중앙값

Variance (분산)

편차(값과 평균의 차이)의 제곱의 합을 자료의 수로 나눈 값입니다.

import statistics

statistics.variance(a)  # 분산
statistics.pvariance(a)  # 모분산

Standard Deviation (표준편차)

분산의 양의 제곱근입니다.

import statistics

statistics.stdev(a)  # 표준편차
statistics.pstdev(a)  # 모표준편차

import numpy

numpy.var(a) # 모분산
numpy.std(a) # 모표준편차

numpy.var(a, ddof=1) # 분산
numpy.std(a, ddof=1) # 표준편차

ddof (Delta Degrees of Freedom)

분모의 n-1 부분에서 1을 담당합니다.

range (범위)

자료를 정렬하였을 때 가장 큰 값과 가장 작은 값의 차이입니다.

max(a) - min(a)

Quartile (사분위수)

전체자료를 정렬했을 때, 1/4, 2/4, 3/4 위치에 있는 숫자를 말합니다. (대략적인 숫자입니다.)

import numpy

numpy.quantile(a, .25)
numpy.quantile(a, .5)
numpy.quantile(a, .75)

numpy.quantile(a, .60) 
# 0-1 사이 아무값이나 들어가도 됩니다. 
# (왼쪽 60% 오른쪽 40%의 값입니다)

사분위수를 사용하면 어느정도 대략적인 모습을 파악할 수 있습니다.

사분위범위(IQR, interquartile range) = Q3 - Q1

numpy.quantile(a, .75) - numpy.quantile(a, .25)

Z-score

어떤 값이 평균으로부터 몇 표준편차 떨어져있는지를 의미하는 값입니다.

import scipy.stats

scipy.stats.zscore(a)
scipy.stats.zscore(a, ddof=1)

ddof (Delta Degrees of Freedom)

분모의 n-1 부분에서 1을 담당합니다. 주어진 데이터가 모집단이냐, 아니면 표본이냐의 차이에 따라 다른값을 계산해주면 됩니다.