저번 포스트에서 Elliptic curve cryptography의 근간이 되는 유한체 상에서 정의되는 타원곡선의 수학적 성질과, 타원곡선 상에서 정의되는 discrete logarithm 문제에 대해 살펴보았습니다.
이번 포스트에서는 타원곡선 상에서 정의되는 discrete logarithm 문제를 풀기 어렵다는 사실을 이용하는 ECDH(Elliptic Curve Diffie-Hellman)와 ECDSA(Elliptic Curve Digital Signature Algorithm)에 대해 알아보겠습니다.
Domain parameters
유한체 상의 타원곡선을 정의하기 위한 값들을 domain parameter라고 합니다.
- : 유한체의 크기를 나타내는 prime number
- : 타원곡선의 coefficients ()
- : 타원곡선 상의 점들의 subgroup의 generator
- : G에 의해 generate되는 subgroup의 order
- : G에 의해 generate되는 subgroup의 cofactor
- : verifiably random한 curve를 generate하기 위한 seed
Random curve
대부분의 elliptic curve 상에서는 discrete logarithm 문제를 풀기 어렵지만, 특정 curve에 대해서는 polynomial time 내에 discrete logarithm 문제를 풀 수 있는 algorithm이 알려져 있습니다.
만약 elliptic curve의 제공자가 해당 curve의 취약점을 미리 간파하고 있다면, 해당 curve는 사용할 수 없을 것입니다. 이러한 문제를 해결하기 위해, seed라는 domain parameter를 사용합니다. 이 seed를 hash한 값을 이용해 domain parameter의 를 생성함으로써, curve의 제공자가 악의적으로 취약한 elliptic curve를 제공하는 것을 방지할 수 있습니다.
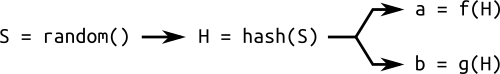
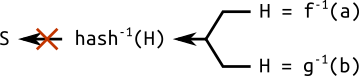
이렇게 생성한 elliptic curve를 verifiably random이라고 합니다.
Elliptic curve cryptography
Domain parameter가 주어졌을 때, elliptic curve cryptography system의 public key와 private key를 다음과 같이 정의할 수 있습니다.
- private key는 중에서 random한 수 d입니다. 은 subgroup의 order입니다.
- public key는 private key가 로 주어질 때 입니다. 는 subgroup의 generator입니다.
Elliptic curve cryptography를 기반으로 하는 ECDH(Elliptic curve Diffie-Hellman), ECDSA(Elliptic Curve Digital Signature Algorithm)에 대해서 알아 보겠습니다.
ECDH
ECDH는 Elliptic curve cryptography를 통해 multiple party 간에 안전하게 key를 합의할 수 있는 key-agreement protocol입니다. Alice와 Bob이 안전하게 key를 합의하고 싶습니다. ECDH 알고리즘은 다음과 같이 이루어집니다.
- Alice와 Bob이 각각 (public key, private key) 쌍을 생성합니다. Alice와 Bob의 키 쌍을 각각 , 라고 하겠습니다. , 입니다.
- Alice와 Bob이 서로의 public key를 교환합니다.
- Alice는 를 계산하고, Bob은 를 계산합니다. Alice와 Bob이 계산한 는 서로 같습니다. Alice와 Bob은 secret key를 공유합니다.
Alice와 Bob이 key를 공유하는 과정에서 , 가 유출되도, 이를 통해 , 를 알아내는 것이 매우 어렵고(discrete logarithm 문제), 합의된 key를 알아내는 것 또한 매우 어렵습니다.
ECDSA
ECDSA(Elliptic Curve Digital Signature Algorithm)는 elliptic curve cryptography를 통해 전자서명을 구현하는 알고리즘입니다.
Alice가 특정 메시지를 자신의 private key로 서명하면, 서명한 값을 Alice의 public key로 검증하려면 어떻게 해야 할까요?
특정 메시지가 주어졌을 때, ECDSA는 먼저 이 메시지를 cryptographic-secure hash function으로 hash화 합니다. 그리고 hash화 된 메시지의 bit length가 domain parameter 과 동일해질 때까지 truncate합니다. 이렇게 생성된 메시지를 라고 하겠습니다.
ECDSA에서 서명을 생성하는 과정은 다음과 같습니다.
- 에서 random number 를 선택합니다. 은 subgroup의 order입니다.
- 를 계산합니다. 는 subgroup의 generator입니다.
- 을 만족하는 을 계산합니다. 는 점 의 -좌표입니다.
- 만약 이면, 를 다시 선택하고 위 과정을 반복합니다.
- 을 계산합니다.
- 만약 이면, 를 다시 선택하고 위 과정을 반복합니다.
위 과정이 끝나면 를 서명값으로 사용합니다.
과정 5에서 을 계산할 수 있어야 하기 때문에, 이 prime number임이 보장돼야 합니다.
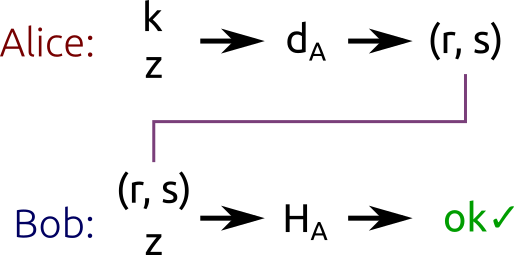
ECDSA에서 서명을 검증하는 과정은 다음과 같습니다.
- 를 계산합니다.
- 를 계산합니다.
- 를 계산합니다.
이면, 유효한 서명임을 검증할 수 있습니다.
Correctness of ECDSA
ECDSA algorithm의 correctness가 어떻게 보장되는지 살펴보겠습니다. 간단한 수식을 통해 이를 확인할 수 있습니다.
서명을 생성할 때, 이었으므로, 임을 알 수 있습니다.
따라서 만약 서명값이 올바르게 생성됐다면, 가 성립함을 알 수 있습니다.

ECDSA에서 z가 무엇인가요?