[백준] 1854번 K번째 최단경로 찾기 ★

💡문제접근

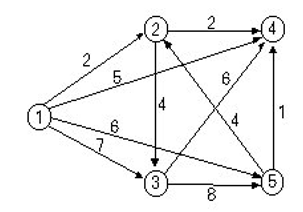
• 테스트케이스에 나온 그래프 정보를 위와 같이 표현할 수 있다.
• 개선된 다익스트라 알고리즘 소스코드에서 변형
• K번째 수를 구하려면 K 이하의 모든 최단 경로를 알아야하므로 a → b로 가는 배열의 크기를 K × (N+1) 크기의 2차원 리스트를 사용하면 된다.

💡코드(메모리 : 66988KB, 시간 : 2736ms)

import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)	# 무한을 의미하는 값으로 10억을 설정

# n : 도시들의 개수(정점), m : 도시 간에 존재하는 도로의 수(간선), k번째
n, m, k = map(int, input().strip().split())
# 출발 노드
start = 1
# 그래프의 각 정점과 인접한 노드들을 연결한 정보를 2차원 리스트에 저장
graph = [[] for _ in range(n+1)]
# 원하는 것은 k번째이므로
distance = [[INF] * k for _ in range(n+1)]

for _ in range(m):
	# a : 출발 도시, b : 도착 도시, c : 시간
    a, b, c = map(int, input().strip().split())
    # a → b로 이동할 때 c만큼의 시간이 발생
    graph[a].append([b, c])

def dijkstra(start):
    queue = []
    # (거리, 노드)의 정보를 우선순위 큐에 삽입
    heapq.heappush(queue, (0, start))
    # 자기 자신 노드에서 자기 자신 노드로의 이동거리는 0
    distance[start][0] = 0
    while queue:
        dist, now = heapq.heappop(queue)
        # 각 정점에 대해 인접한 노드들에 대해서
        for i in graph[now]:
            cost = dist + i[1]
            if cost < distance[i[0]][k-1]:
                distance[i[0]][k-1] = cost
                distance[i[0]].sort()
                heapq.heappush(queue, (cost, i[0]))

dijkstra(start)

for i in range(1, n+1):
    if distance[i][k-1] == INF:
        print(-1)
    else:
        print(distance[i][k-1])

💡소요시간 : 1h