[C] 백준 11051번 이항 계수 2

링크
https://www.acmicpc.net/problem/11051

문제

---

자연수 $N$과 정수 $K$가 주어졌을 때 이항 계수 $\begin{pmatrix} N\\ K \end{pmatrix}$를 10,007로 나눈 나머지를 구하는 프로그램을 작성하시오.

입력

---

첫째 줄에 $N$과 $K$가 주어진다.$(1≤N≤1,000, 0≤K≤N)$

출력

---

$\begin{pmatrix} N\\ K \end{pmatrix}$를 10,007로 나눈 나머지를 출력한다.

예제 입력 1

---

5 2

예제 출력 1

---

10

아이디어 스케치

---

이항 계수를 동적계획법 알고리즘을 이용해서 푸는 문제이다.
동적계획법 알고리즘을 사용하기 전 기반 상황과 일반 상황을 살펴보겠다. 기반 상황이란 답이 이미 알려진 가장 작은 부분 문제이고, 일반 상황이란 기반 상황을 제외한 모든 상황이다.

기반 상황

• $C(n,0) = 1$ => $n$개에서 하나도 뽑지 않은 경우는 한가지
• $C(n,n) = 1$ => $n$개에서 $n$개를 뽑는 경우도 한가지

일반 상황

• $n$번째 항목을 포함하는 경우 : $C(n-1, k-1)$
• $n$번째 항목을 포함하지 않는 경우: $C(n-1, k)$

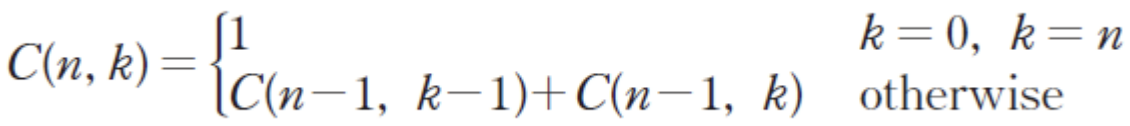
위 기반 상황과 일반 상황을 바탕으로 순환관계식을 위와 같이 작성할 수 있다.

C(5,3)으로 작성한 동적계획법 테이블이다.

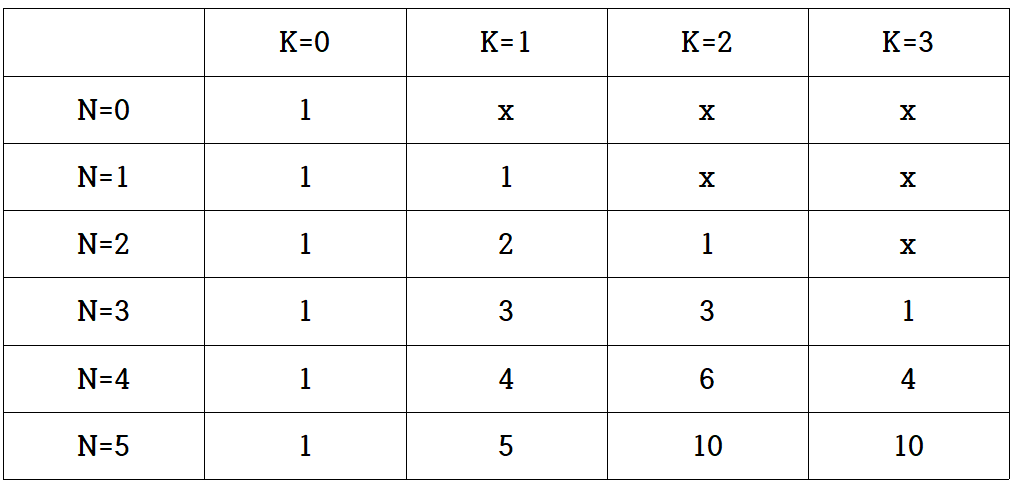
이 테이블에서 X는 고려하지 않는 칸이다. 즉 n보다 k가 큰 경우에는 아예 고려하지 않는다.

전체 코드

---

#include <stdio.h>
#include <stdlib.h>
#define mod 10007

#define min(a, b) ((a) > (b) ? (b) : (a))

int main() {
    int N, K;
    int i, j;
    int** dp;

    scanf("%d %d", &N, &K); // N과 K를 입력받음

    // 메모리 동적 할당
    dp = (int**)calloc(N + 1, sizeof(int*));
    for (i = 0; i <= N + 1; i++) {
        dp[i] = (int*)calloc(K + 1, sizeof(int*));
    }

    for (i = 0; i <= N; i++) {
        for (j = 0; j <= min(i, K); j++) {      //min(i, K)의 의미는 n<k의 경우를 고려하지 않는다는 뜻
            if (j == 0 || j == i) {     // k가 0이거나 n과 같은 경우(기반 상황)
                dp[i][j] = 1;
            }
            else {      // 일반 상황
                dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % mod;
            }
        }
    }

    printf("%d", dp[N][K]); // 결과 출력

    // 메모리 해제
    free(dp[0]);
    free(dp);

    return 0;
}

제출 결과

---