Large-Margin Contrastive Learning with Distance polarization Regularizer (ICML / 2021) paper review

Contribution

• metric learning의 pairwise distribution의 특성으로부터 영감을 받아, distance polarization을 이용한 large-margin contrastive learning에 대하여 제안하였다.

• 유사도 측정과 downstream classification에 대한 error bound 분석에 대한 충분한 이론적 증명을 제공한다.

• synthetic, image, NLP, 강화학습 task에서 state-of-the-art보다 좋은 성능을 보여주었다.

---

Background : Contrastive Learning

• unsupervised / self-supervised learning approach로서, contrastive learning의 주요 목적은 intrinsic feature를 잘 추출해내기 위하여 data point를 m-dimensional space에서
  d-dimensional space로 transform하는 feature embedding을 학습하는 것이다.

• instance discrimination이라고도 불리우는 Contrastive Learning은 보통 training data에서 두 instance의 pair를 멀게 함으로써 embedding을 학습한다.

• Contrastive Learning의 효과는 다음 두 component에 영향을 받는다.
  - positive pairs (x, x+)
  single instance x와 perturbation을 적용한 x+로 구성된다.
  - negative pairs (x, x-)
  training data에서 두 original instance로 구성된다.
  

• 다음 NCE Loss는 Contrastive Learning에서 자주 사용되는 Loss이다.
  

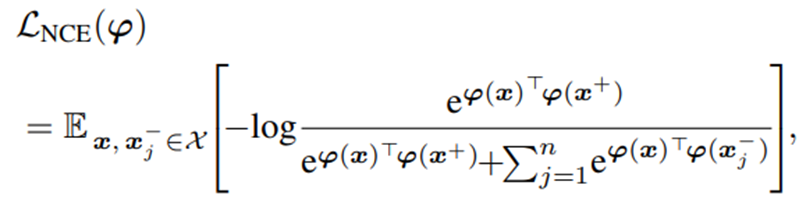
• 이 논문에서는 이러한 NCE Loss가 모든 negative pair를 멀어지게 함으로써 semantically similar한 data pair 역시도 멀어지게 하는 false-negative 문제를 야기할 수 있다고 주장하고 있다.

• 그래서 이러한 문제를 해결하기 위하여 metric learning의 basic property를 이용하였다고 한다.

---

Background : Metric Learning

• supervised learning problem에서 metric learning은 sample space내에서 두 instance간의 pair-wise similarity를 잘 측정하기 위한 distance metric을 학습하는 것을 목표로 한다.

• 이러한 metric learning에서는 (n+1)-tuplet loss가 자주 사용이 된다. 이 loss는 intra class distance는 작게하고 inter class distance는 크게 하는 것을 목표로 하고있다.
  

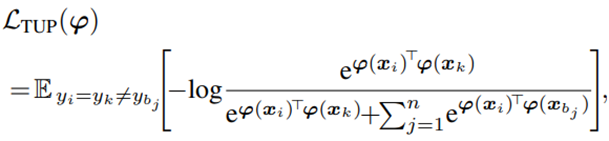
• 이러한 learning objective를 minimize하는 것은 intra class와 inter class distance간에 margin을 형성하게 되고, 그러므로 두 original instance간의 pairwise similarity를 잘 측정할 수 있게 된다.
  (inter class끼리는 가까워지게, intra class끼리는 멀어지게 학습)

• 이 논문에서는 metric learning model의 이러한 basic property를 Contrastive Learning의 loss를 제어하는 regularizer로서 이용하였다.

---

Motivation

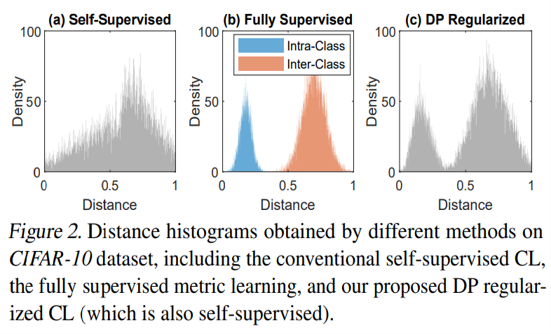
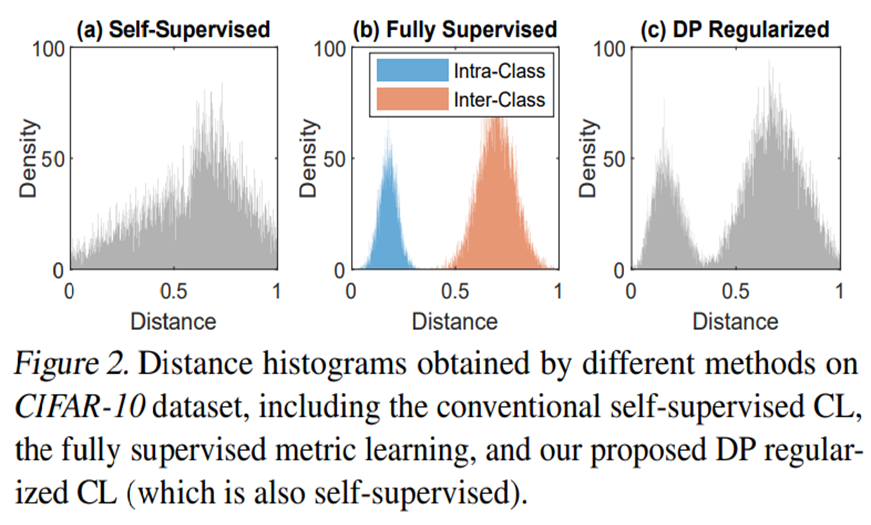
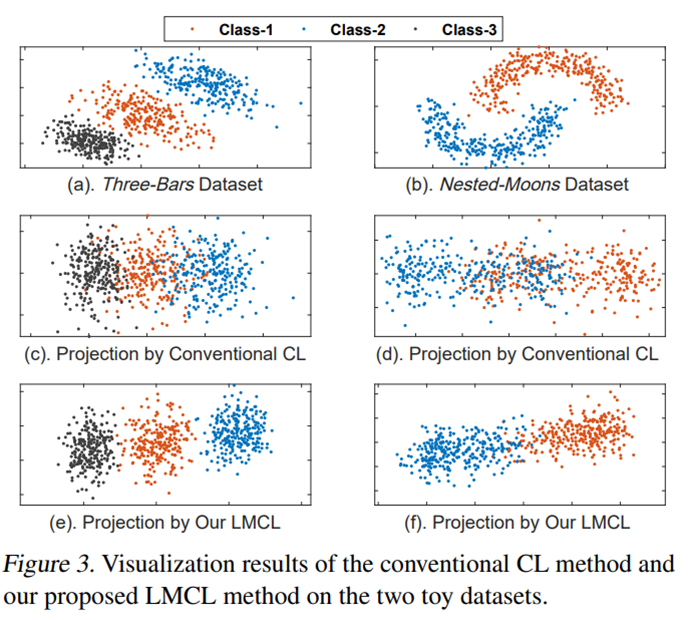
• 다음 figure는 각각 (a) self-supervised contrastive learning, (b) fully supervised metric learning, (c) self-supervised contrastive learning with proposed DP regularizer의 euclidian distance distribution histogram이다.
  

• Euclidean distance는 두 sample간의 (dis)similarity를 측정한다. 두 sample이 유사할수록 distance는 작은 값을 가지게 된다.

• Contrastive Learning은 각 pair의 instance간 거리를 벌리는 것을 목표로 한다. (즉, original sample간의 거리가 1이 되도록 하는 것을 목표로 함. 이 과정에서 discard되는 pair들이 semantically positive pair로 구분 가능하다.) 그렇지만 위의 figure를 보면 (a)의 경우 분포가 margin없이 전반적으로 퍼져 있고, 0.5부근에 많은 값이 존재하는 것을 확인할 수 있다. 이는 기존의 contrastive learning이 instance discrimination을 위하여 distance space간 large margin을 확보하는 것에 실패하였음을 의미하고 있다.

• 반면 이 논문에서 제안하는 DP regularizer를 사용하였을 경우에는 (b)처럼 이상적으로 가운데 margin을 두고 positive pair, negative pair분포가 나뉘어진 것을 확인할 수 있다.

---

Motivation with proof

• 아래 식들을 통하여 위의 Motivation에서 본 현상을 수식적으로 증명할 수 있다.

• 우선 위에서 본 euclidian distance는 다음과 같이 식의 변형이 가능하다.
  
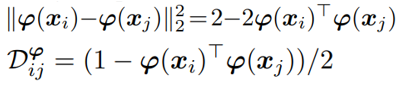
  그리고 feature embedding pi가 있다고 가정한다.
  
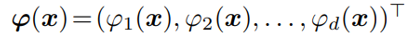
  euclidian distance에 대하여 expectation을 취한 후, sample 수 N을 무한대로 보내면 distance가 1/2로 수렴하게 된다.

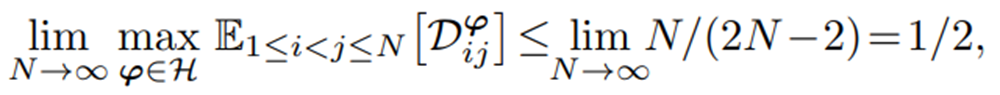
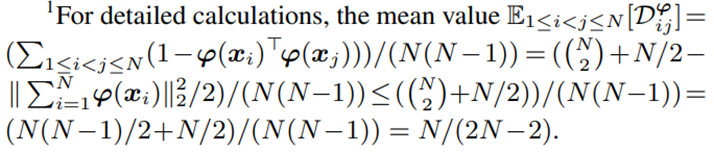
• 이는 즉 pairwise distance의 mean value가 ideal value인 1이 아니라 1/2로 enlarge됨을 의미한다.

• 또한 다음 Theorem 1을 통하여 기존의 Contrastive Learning이 0과 1 사이에 전반적으로 분포하게 됨을 보여준다. (다음 식의 구체적인 증명은 본 논문의 supplementary material를 통하여 확인할 수 있다.)
  

---

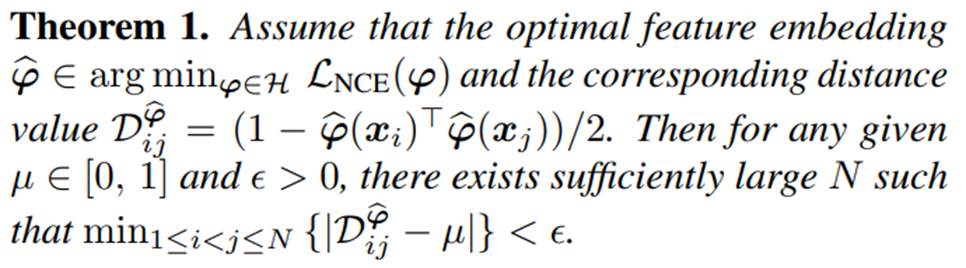
Formulation

• 앞에서 봤듯이, distance space [0, 1]은 점차 pairwise distance들로 덮이게 되고, 결국 similar & dissimilar pair들을 명확하게 나누어주는 margin region을 잃게 된다.

• 그렇지만 supervisory information을 사용하게 되면, metric learning으로부터 얻은 intra-class와 inter-class distance가 (metric learning algorithm이 intricsic feature를 포착할 수 있게 하기 위하여) 명확한 margin region을 통하여 구분되게 된다.

• 대부분의 metric learning은 앞서 말했다시피, inter-class distance는 크게 하고 intra-class distance는 작게하여 intra-class와 inter-class간에 margin region을 생성한다.

• 이는 곧 metric learning을 통하여 얻은 final distance가 중간에 margin region을 갖는 양극화된 분포일 것을 의미한다.

---

Formulation : Distance Polarization (DP) Regularizer

• 이 논문에서 제안하는 Distance Polarization Regularizer에 대하여 살펴보자면, 우선 pairwise distance matrix DΦ와 0 < δ+ < δ- < 1의 크기 순서를 가지는 δ+, δ- 가 있다고 가정한다. 여기서 intra-class distance들은 δ+보다 작고, inter-class distance들은 δ-보다 커야한다고 가정한다.

• 이러한 가정 하에 다음과 같은 regularizer를 정의할 수 있다.
  

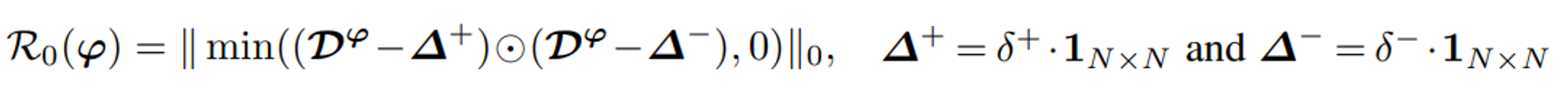
• 이러한 reglularizer를 minimize하는 것은 모든 pairwise distance들이 [0, δ+] 영역 혹은 [0, δ-] 영역에 분포하도록 유도한다. 만약 pairwise distance가
  [δ+, δ-] 사이의 영역에 존재하게 된다면 regularizer 속 식이 음의 값을 갖게 되고 결과적으로 regularizer가 양의 값을 가지게 된다. (regularizer가 loss를 키우게 되는 결과를 가져옴) 이를 막기 위하여 model은 [δ+, δ-] 사이 영역이 distribution의 margin이 되도록 학습될 것이다.

• 최종적으로 이 논문에서 제안하는 Large-Margin Contrastive Learning model의 loss는 다음과 같다.
  

---

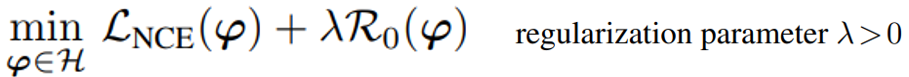
Formulation : Determination of Δ+ and Δ-

• 다음으로 Δ+와 Δ-의 정의에 대한 설명이다.

• 우선 τ = δ- - δ+ 를 tuning가능한 parameter로 놓는다. 그렇게 되면 δ- 값만 지정해주면 된다.

• 아래 Theorem 2를 통하여 δ-가 1/2이 되는 것이 (0, 1/2) 구간에 속하는 margin width τ를 얻기 좋은 값이라는 것을 증명하고 있다.

---

Formulation : Optimization

• 그 다음으로 dp regularizer의 optimization에 대한 설명이다.

• 우선 Final loss를 다음과 같이 stochastic form으로 변환하여 준다. (추가 적인 설명은 논문과 supplementary material 참고)
  

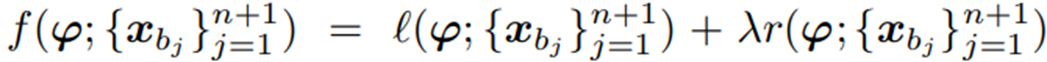
• 그리고 Adam optimizer를 통하여 optimization을 수행하게 되면 다음
  Eq. (11)에서 볼 수 있듯이 stochastic gradient 계산만큼의 computational overhead가 들게 된다.
  

• 이를 통하여 DP regularizer를 사용하는 것이 기존의 contrastive learning method에 쉽게 implementation이 가능하고 매우 작은 양의 computational overhead 밖에 들지 않음을 보여주고 있다.

---

Experiments

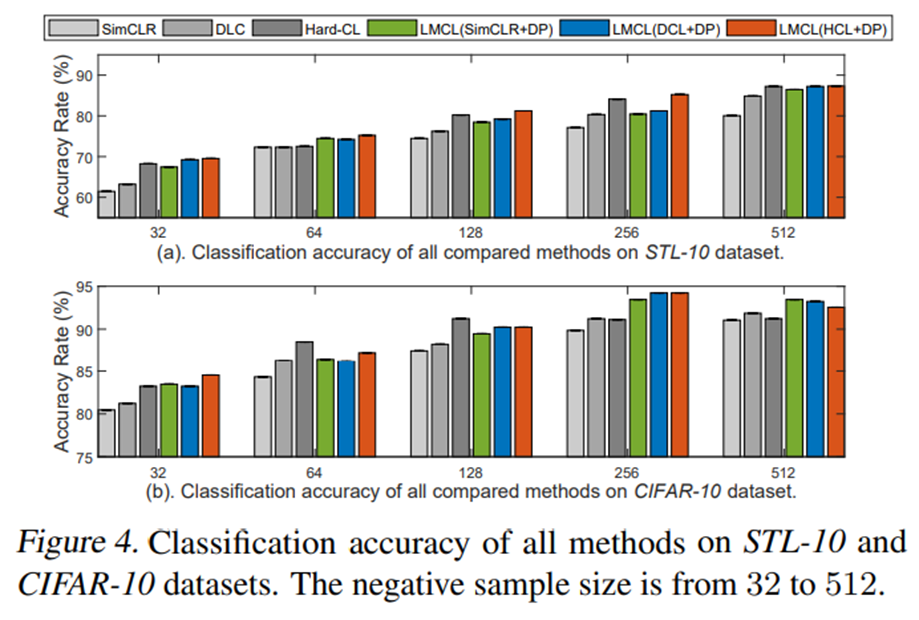
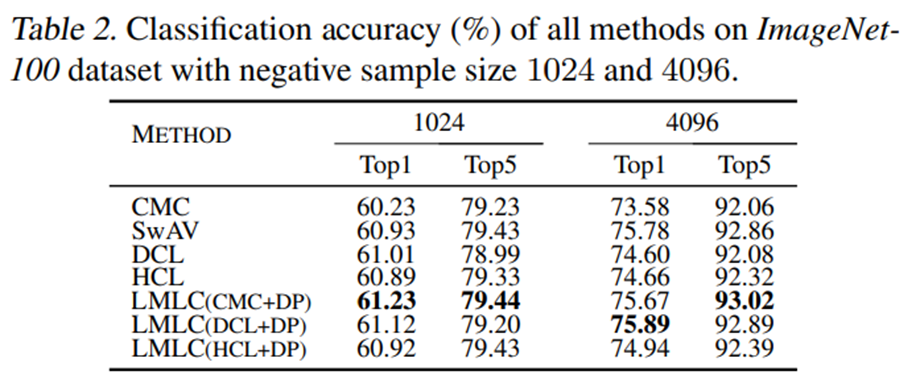
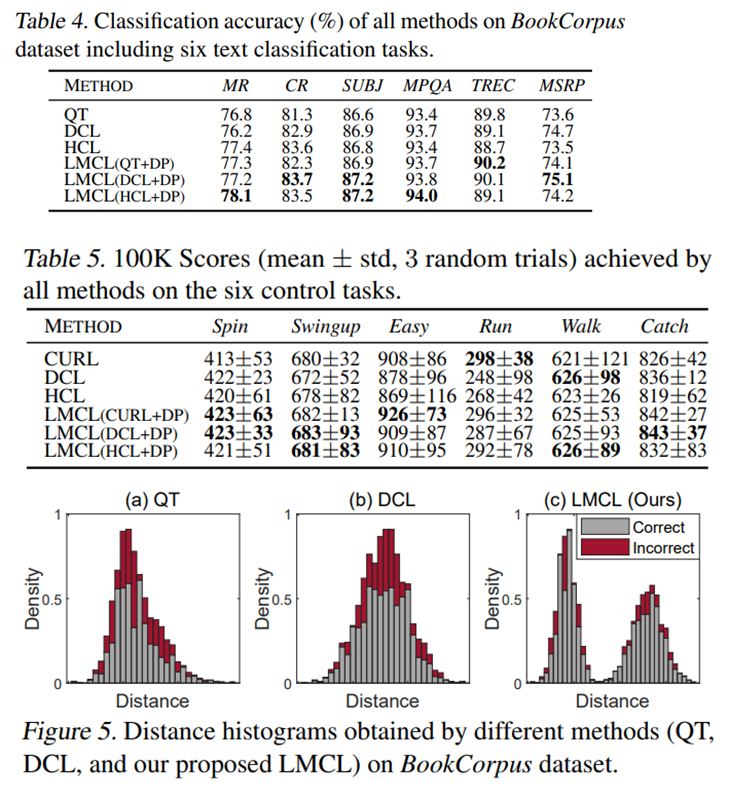
• 대부분의 task에서 다 state-of-the-art보다 좋은 성능을 보여주고 있다. 특히 Figure 5는 text classification에서 기존의 contrastive learning을 사용하였을 때보다 DP regularizer를 사용하였을 때 positive와 negative pair들이 bimodal 양상을 띠며 분리되어 있는 모습을 확인할 수 있다.

---

Conclusion

• 이 논문에서는 기존의 Contrasitve Learning algorithm이 semantically similar & dissimilar한 data pair를 구분하기 위하여 distance space내에 margin region을 확보하는 것에 실패하였음을 보여주고 있다.

• 이 논문에서는 양극화된 distance를 야기하는 DP regularizer를 제안하였으며 그를 통해 unsupervised 방식으로 distance space내에서 large margin을 확보하였다.

• 또한 이 논문은 제안하는 method에 대하여 다양한 theoretical analyses를 제공하고 있다. (추가적인 analysis는 논문과 supplementary 참고)