퍼셉트론이란?
- 다수의 신호를 입력으로 받아 하나의 신호로 출력하는 것.
- 이때 신호란 전류나 강물처럼 흐름이 있는 것
- 퍼셉트론의 신호는 흐른다(1)/안 흐른다(0) 두 가지 값을 가지고 있음
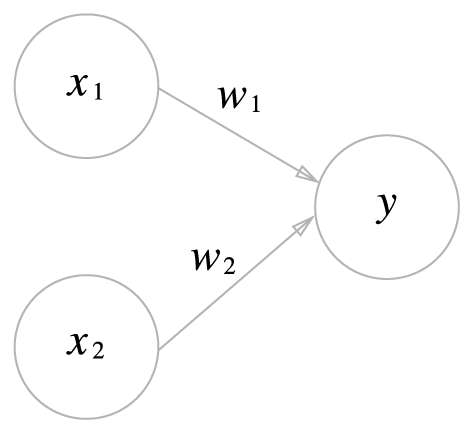
- 과 는 입력신호, 는 출력신호, 과 는 가중치(weight)를 뜻함.
- 원은 뉴런 또는 노드라고 말함.
- 입력 신호가 뉴런에 보내질 때 각각 고유한 가중치()가 곱해진다.
- (, )의 합이 정해진 한계를 넘어설 때 1을 출력하며 이때 '뉴런이 활성화 된다.'라고 표현한다.
- 그 정해진 한계를 임계값이라고 하며 기호로 나타낸다.
수식으로 나타내면 아래와 같다.
수식 1
- 퍼셉트론은 각 입력신호마다 고유한 가중치를 부여하고 각 신호가 결과에 주는 영향력을 조절한다.
- 가중치가 클수록 강한 신로를 흘려보냄. (입력 신호와 곱셈으로 작용하기 때문)
단순한 논리 회로
AND 게이트
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- 모두 1일 때만 1을 출력하고 나머지는 0을 출력
NAND 게이트
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- AND 게이트를 구현하는 매개변수의 부호를 모두 반전하면 NAND 게이트가 된다.
- 두 개의 신호 모두 1이 아닌 경우에만 1을 출력한다.
OR 게이트
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- 두 입력 신호중 하나라도 1이면 1을 출력한다.
퍼셉트론 구현하기
간단한 구현
# AND 게이트
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
print(0)
else:
print(1)
AND(0, 0) # 0
AND(0, 1) # 0
AND(1, 0) # 0
AND(1, 1) # 1가중치와 편향 도입
위의 수식 1의 를 -b(편향, bias)로 치환하면 밑의 식처럼 된다.
편향(bias): 결정 경계(분류 기준)를 평행 이동(shift) 시켜주는 역할을 함.
본래 원점을 지나야 하는데 평행 이동을 할 수 있어, 원점 근처에 없는 데이터들도 분석이 가능함.
수식 2
- 여기서 b를 편향이라고 하며 와 는 그대로 다중치다.
- 입력 신호에 가중치를 곱한 값과 편향을 합한 값이 0을 넘으면 1을 출력한다.
이 식을 파이썬 코드로 구현해보았다.
import numpy as np
x = np.array([0, 1]) # 입력
w = np.array([0.5, 0.5]) # 가중치
b = -0.7 # 편향
print(x*w) # [0. 0.5]
print(np.sum(w*x)) # 0.5
print(np.sum(x*w)+b) # -0.19999999999999996 (부동소수점에 의한 연산 오차)가중치와 편향 구현하기
가중치와 편향을 도입한 AND 게이트는 다음과 같음
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(x*w) + b
if tmp <= 0:
print(0)
else:
print(1)b가 -0.1이면 각 신호에 가중치를 곱한 값의 합이 0.1을 초과할 때 뉴런이 활성화 됨.
-20이면 합이 20을 초과할 때 뉴련이 활성화 됨.
NAND와 OR는 아래와 같다.
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # AND와는 가중치(w)와 편향(b)가 반대다.
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
print(0)
else:
print(1)
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # AND와는 가중치(w)와 편향(b)가 반대다.
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
print(0)
else:
print(1)
NAND(0, 0) # 1
NAND(1, 0) # 1
NAND(0, 1) # 1
NAND(1, 1) # 1
OR(0, 0) # 0
OR(1, 0) # 1
OR(0, 1) # 1
OR(1, 1) # 1퍼셉트론의 한계
XOR 게이트
XOR 게이트는 베타적 논리합입니다. 진리표는 아래와 같습니다.
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
지금까지 본 퍼셉트론으로는 XOR 게이트를 구현할 수 없다.
일 때 아래의 식처럼 된다.
수식 3
이 식은 직선으로 두 영역을 만들고 한 쪽 영역은 1, 다른 한 쪽은 0이 된다.
그것을 그림으로 그려보면 아래와 같다.
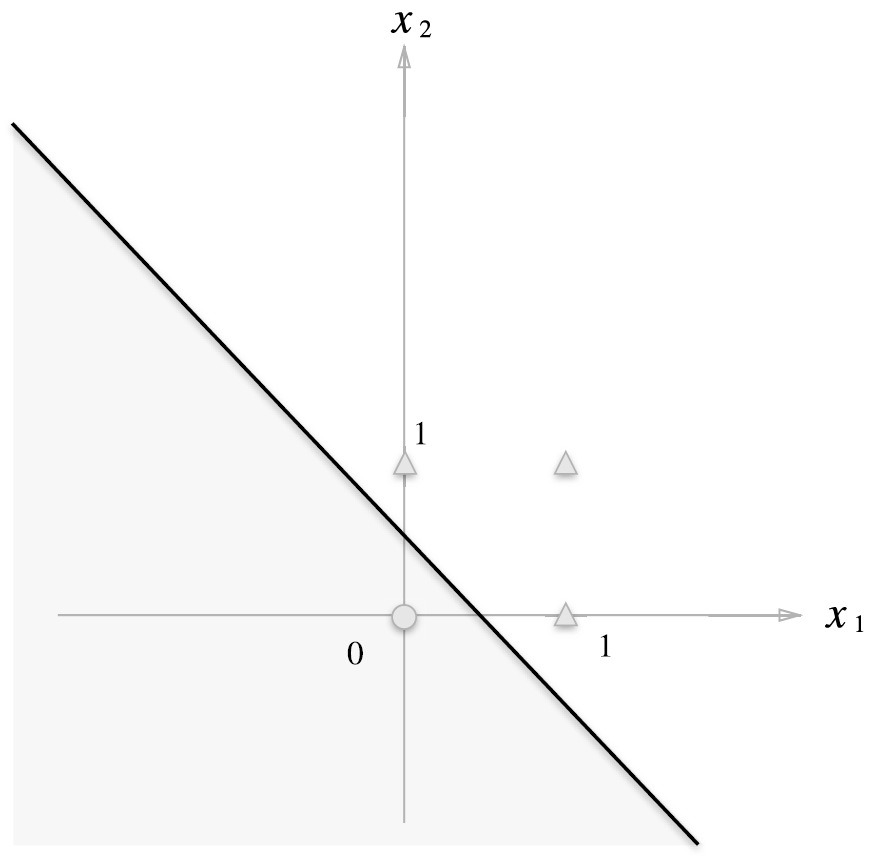
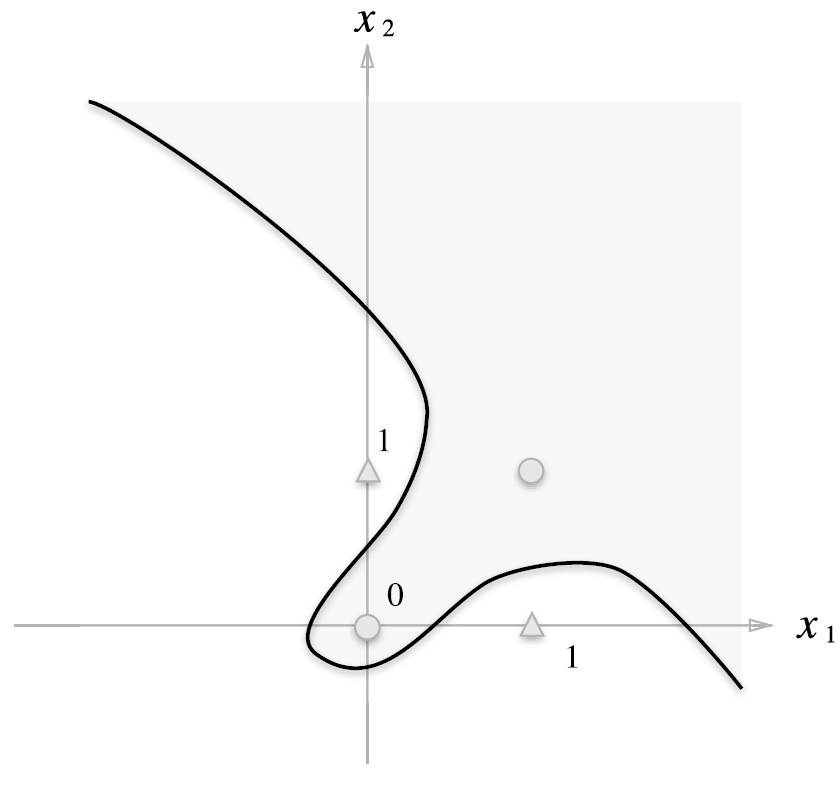
퍼셉트론의 시각화: 회색 영역은 0, 전체 영역은 OR 게이트 성질을 만족한다.
출처: https://github.com/youbeebee/deeplearning_from_scratch/tree/master
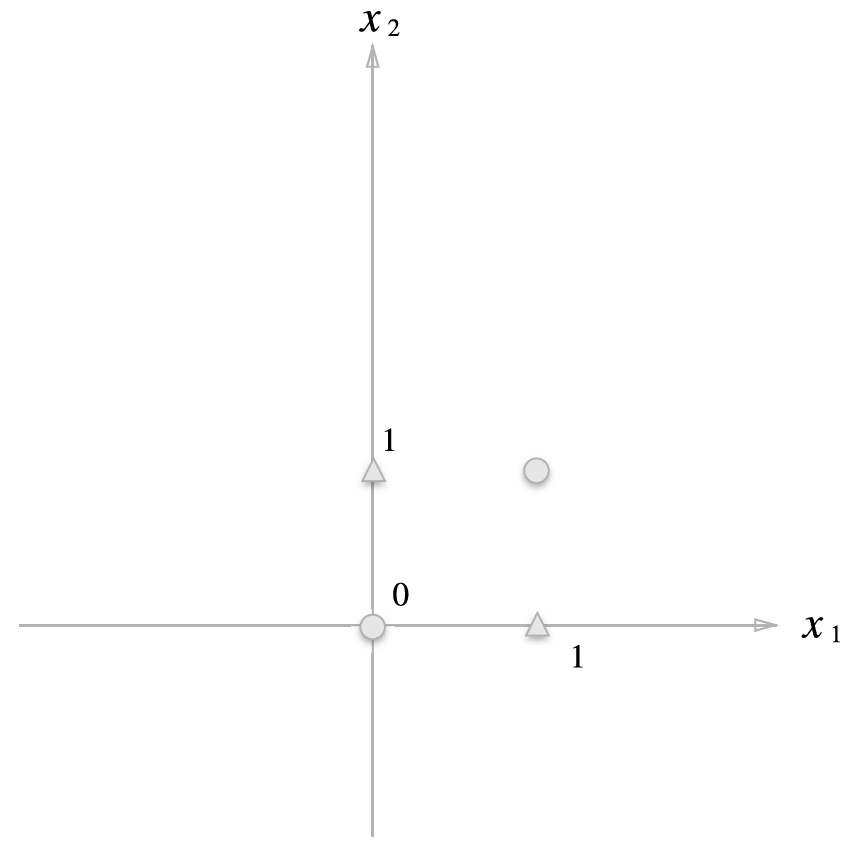
OR 게이트는 (0,0)일 때 0을 출력하고 나머지 경우에는 1을 출력한다.
출력값이 0일 때 ●, 1일 때 ▲으로 표시했다.
OR 게이트를 만들려면 삼각형과 원형을 직선으로 나누어야 한다.
위 그림은 직선으로 나눈것을 볼 수 있다.
그렇다면 XOR 게이트는 어떨까?
이 그림에서 하나의 직선으로 삼각형과 원형의 영역을 나누라고 하면 불가능하다라 생각이 든다.
선형과 비선형
위 XOR 게이트의 그림은 직선으로는 절대 나눌 수 없다.
하지만 직선이 아니라 곡선이면 가능하다.
이처럼 직선 영역을 선형, 곡선을 비선형 영역이라고 한다.
다층 퍼셉트론
그래서 퍼셉트론으로는 XOR게이트를 표현할 수 없다.
하지만 다층 퍼셉트론이라면 가능하다.
기존 게이트 조합하기
그리고 그 AND, NAND, OR 게트트를 조합하여 XOR 게이트를 만들 수 있다.
앞에서 말한 퍼셉트론은 '단층 퍼셉트론이다' 단층 퍼셉트론은 직선으로 영역을 나누고 XOR 게이터를 표현할 수 없다.
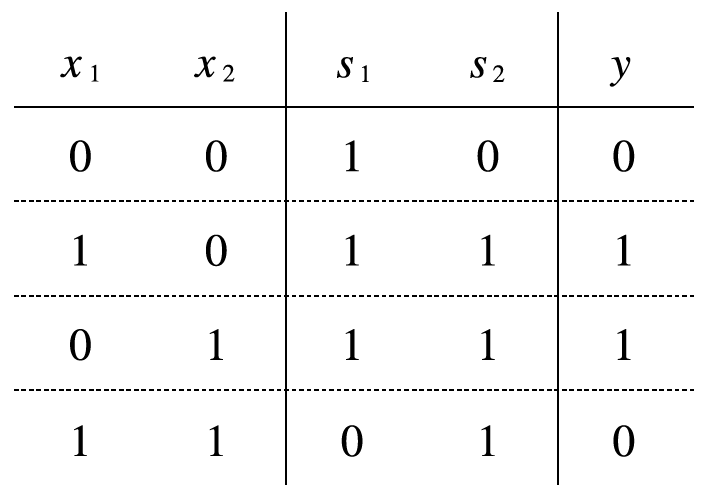
AND, NAND, OR 게이트로 만든 XOR 게이트 진리표
출처: https://github.com/youbeebee/deeplearning_from_scratch/tree/master
이것을 이용하여 XOR 게이트를 구현했다.
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
print(y)
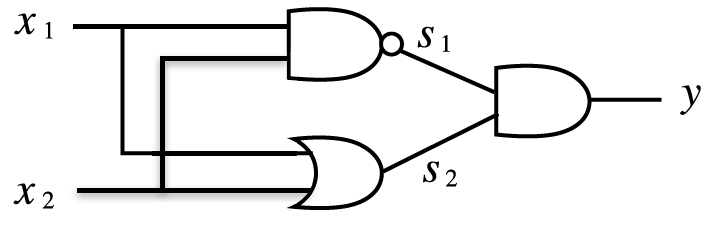
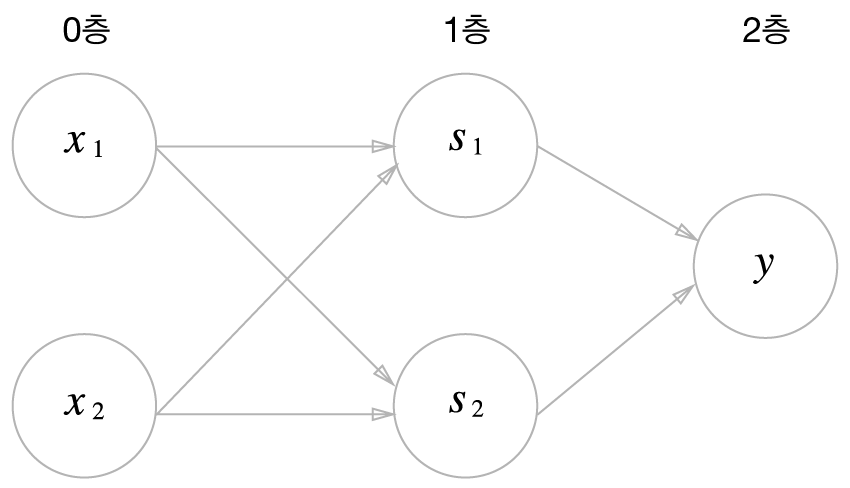
return y그리고 이 XOR게이트의 퍼셉트론 그림은 아래와 같다.
현재 그림에서는 3개의 층으로 나오지만 가중치를 같는 층은 2개(0~1층, 1~2층)다.
그래서 2층 퍼셉트론이라고 부른다. 문헌에 따라서 3층 퍼셉트론이라고 하는 경우도 있다.
위 그림을 해석하자면
1. 0층의 두 뉴런이 입력신호를 받아 1층의 뉴런으로 신호를 보낸다.
2. 0층에서 보낸 신호를 두 뉴런이 받아 2층의 뉴련으로 신호를 보낸다.
3. 1층에서 보낸 신호를 받은 2층 뉴런은 y값을 출력한다.
정리
- 퍼셉트론이란 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 알고리즘에 따라 값을 출력한다.
- 퍼셉트론에서는 가중치와 편향을 매개변수로 설정한다.
- 퍼셉트론으로 AND, OR, NAND 게이트를 표현할 수 있다.
- 단층 퍼셉트론은 직선으로 영역을 나눈다. 이를 선형 구조라고 한다.
- 단층 퍼셉트론으로는 XOR 게이트를 표현할 수 없다.
- 단층 퍼셉트론을 겹겹이 쌓은 다층 퍼셉트론으로 XOR 게이트를 표현할 수 있다.
- 다층 퍼셉트론은 곡선으로 영역을 나눈다. 이를 비선형 구조라고 한다.