3층 신경망 구현하기
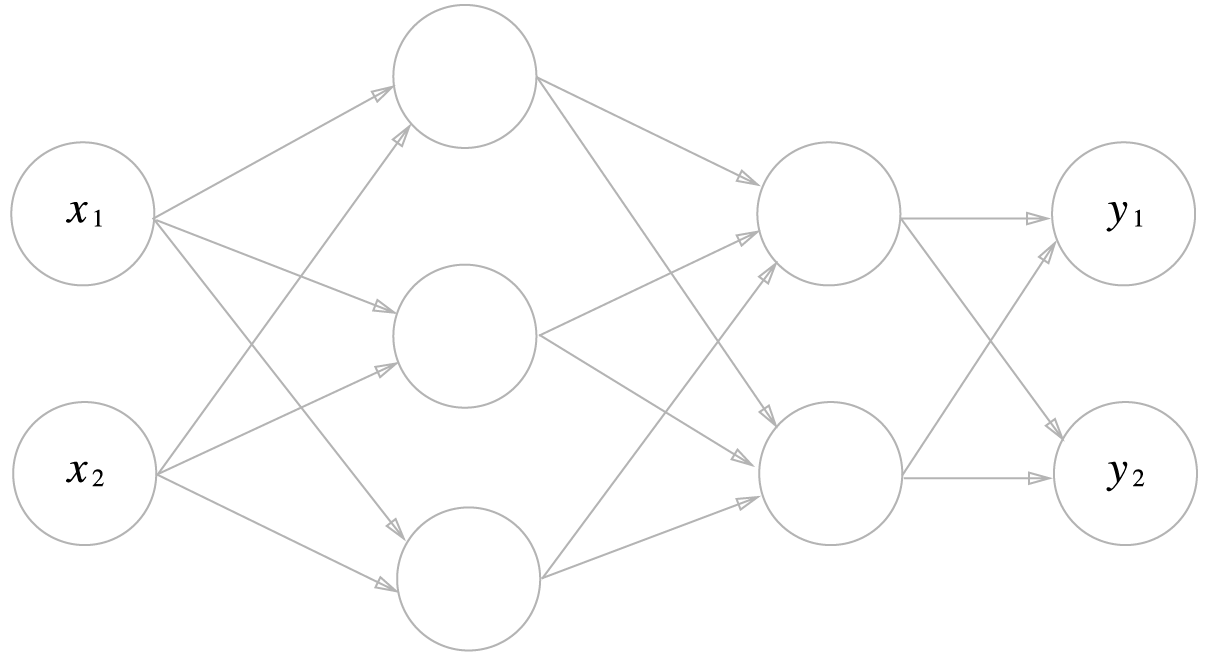
3층 신경망: 입력층 2개 은닉층 3개 은닉층 2개 출력층 2개
출처: https://github.com/youbeebee/deeplearning_from_scratch/tree/master
표기법
아래 그림은 신경망 표기법이다.
그리고 여기에 편향이 합쳐지면 아래의 그림처럼 된다.
편향은 인덱스가 1개밖에 없다.
이렇게 되어 를 수식으로 나타내면 아래와 같다.
수식 1
여기서 행렬의 곱을 이용하면 아래처럼 간소화 할 수 있다.
수식 2
그리고 위 수식을 코드로 표현하면
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
A1 = np.dot(X, W1) + B1 # array([0.3, 0.7, 1.1])이렇게 나온다.
이러면 a1부터 0.3, 0.7, 1.1이 나오는 것이다.
그리고 이 활성화 함수의 처리를 그림으로 나타내면 아래와 같다.
이제 위 그림처럼 활성화 함수로 시그모이드 함수를 사용하여 구현하면
Z1 = sigmoid(A1)
print(A1) # [0.3 0.7 1.1]
print(Z1) # [0.57444252 0.66818777 0.75026011]이렇게 간결하게 나온다.
이제 똑같이 1층에서 2층으로 가는 과정을 그림으로 표현했다.
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
print(Z2) # [0.62624937 0.7710107 ]가중 신호와 편향의 총합을 a로 표기하여 함수 h에 넣고, 그로인해 변환된 신호 z를 다음 신호로 넘긴다.
def identity_function(x):
return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)
print(Y) # [0.31682708 0.69627909]항등 함수인 identiry_function()을 정의하고 이것을 출력층의 활성화 함수로 사용했다. 또한 활성화 함수는 로 표시하여 은닉층의 h()와 다름을 명시했다.
구현 정리
이제 3층 신경망을 통합적으로 정리했다.
관례에 따라 가중치만 대문자로 표혔했다고 한다.
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) # 1층 가중치
network['b1'] = np.array([0.1, 0.2, 0.3]) # 1층 편향
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) # 2층 가중치
network['b2'] = np.array([0.1, 0.2]) # 2층 편향
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]]) # 3층 가중치
network['b3'] = np.array([0.1, 0.2]) # 3층 편향
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = sigmoid(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [0.57855079 0.66736228]이름이 forward인 이유는 순전파임을 알리기 위해서다 만약 역방향이라면 (ackward)라고 칭한다.





