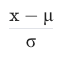[이론 내용만] Node 12. 고객을 세그먼테이션하자!
☺️ AIFFEL 데이터사이언티스트 3기

12-1. 들어가며
학습목표
- 데이터 분석으로 고객 세그먼테이션 진행 방식 및 인사이트 파악하기!
12-2. 이상 데이터 분석 및 처리
이상치?
- dataset 내에서 다른 값들과는 달리 큰 차이가 나는 데이터 포인트
- 클러스터링에서 결과 왜곡을 발생시키기 때문에 적절히 식별하고 처리해야 함!
이상치 데이터는 클러스터링 결과를 어떻게 왜곡하나?
- 클러스터링 : 비슷한 데이터 포인트들을 그룹으로 묶는 것
- 초등학생이지만 키가 많이 큰 학생이 -> 초등학생 그룹의 키 클러스터링 왜곡!
- 홀로 큰 학생이 -> 자신만의 클러스터 형성 가능!
- 즉, 다른 데이터 포인트들을 크게 벗어나면서 명확하게 그룹을 만들 수 없게 만드는 것!
- 특성이 여러 개라면 다차원 공간에서 이상치를 감지하는 알고리즘을 쓰자!
user_data는 Z-Score를 통한 이상치 감지 방법 사용- 각 특성 값들을 표준화
- 그 데이터 포인트가 특성 평균에서 얼마나 표준 편차만큼 떨어져 있는지 분석하는 것!
Z-Score를 활용한 이상치 분석이란?
- 통계적 방법
- 데이터의 각
feature(특성)를 ->mean(평균),standard deviation(표준 편차)로standardization(표준화)하는 것!
표준화?
- 평균 중심 데이터 분포 방법
- 상대적 기준을 갖는 값을 데이터 표준화로 표준정규분포곡선에서 값 비교 가능!
- 이미지 출처 : 도서 '수학의 시작'
- 표준 편차가 낮다 == 데이터 포인트들이 평균 근처에 모여 있다
- 표준 편차가 높다 == 데이터 포인트들이 평균에서 멀리 흩어져 있다 -> 데이터의 분포가 불안정하다는 의미
-
Z-Score
- 일반적인 경우 Threshold(특정 임계값) 설정!
- 임계값 초과 시 이상치로 간주!
- 계산 방법
- 각 feature의 평균과 표준편차 계산
각 데이터 포인트의 해당 특성 값 - 평균을표준 편차로 나누기
- 평균이 0이고 표준 편차가 1인 표준 정규 분포를 기준으로 함.
- 즉, Z-Score > 0 -> 평균보다 큰 값!
- Z-Score < 0 -> 평균보다 작은 값!
정규분포?
- 데이터가 평균 주변에 대칭 분포하는 확률 분포
- 종 모양 곡선
- 평균에 몰려있고, 평균에서 멀어지면 빈도가 줄어듦.
- 표준 정규 분포 : 평균이 0이고 표준편차가 1인 정규 분포!
이상치 찾기
user_data불러오기- pandas 라이브러리 : 데이터 처리 및 분석 라이브러리

- 이상치 라이브러리 불러오기
- Z-score를 계산하는 함수 : scipy의 stats 사용!
- Scipy 라이브러리 : 수치 계산, 최적화, 신호 및 이미지 처리, 선형 대수, 확률 및 통계, 특수 함수 같은 과학 및 수학 연산 수행
- Numpy 라이브러리 : 행렬, 벡터, 배열의 수치 연산 라이브러리
- Z-score를 계산하는 함수 : scipy의 stats 사용!

CustomerID를 제외한 값 정규화 + Z-score 계산- 음수가 있어서 절대값으로 변경!
- 음수가 있어서 절대값으로 변경!
- 임계값 설정
- 임계값 3 정의, Z-Score를 이용한 이상치 감지
- 이상치 식별 후 "outlier"라는 새로운 열에 표시!

3으로 설정 == Z-Score가 3을 넘는다면 outlier(이상치)로 간주!
z-score > 3,z-score < -3데이터는 극단값이라 이상치!
- 이미지 출처 : 아이펠
- 정상 데이터 및 이상치 수 시각화
- 정상 라벨링 : 93.51%
- 이상치 라벨링 : 6.49%

시각화 결과 정리
- 약 6% 고객이 이상치로 식별됨.
- 다음 단계
- 'outlier = 0'인 정상 데이터 유지
- 즉, 'outlier = 1' 이상치 제거
- outlier 컬럼 삭제

- 'outlier = 0'인 정상 데이터 유지
12-3. 변수 간 상관관계 분석
correlation(상관 관계)?
- 통계학
- 두 변수간 관계 강도와 방향
- 한 변수가 변화 -> 다른 변수가 어떤 변화를 보이는지!
- 보통
-1 ~ 1사이 값으로 표현!- 양의 상관관계 : 한 변수 ⬆️, 다른 변수 ⬆️ (광고비 지출과 판매량)
- 음의 상관관계 : 한 변수 ⬆️, 다른 변수 ⬇️ (운동량과 체중 감소)
- 상관 관계 없음 : 아무런 관계 없을 때(관련 없을 때)
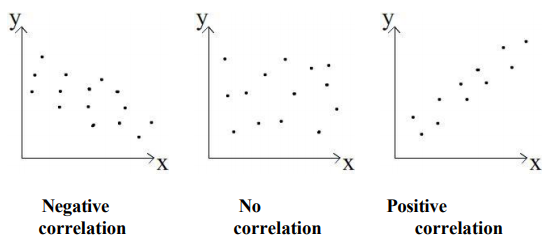
- 출처 : https://analytics17.blogspot.com/2017/08/1-2.html
상관관계 절대값 크기가 클수록 -> 두 변수 사이 관계가 더 강하다!
그러나, 이것이 인과관계를 의미하지 ❌
- 한 변수 변화가 다른 변수 변화를 유발하지는 않는다는 것.
multicollinearity(다중공선성 문제)
-
회귀 분석 시 사용된 모형 일부 예측 변수가 다른 예측 변수와 상관 정도가 높아서 -> 데이터 분석을 할 때 부정적 영향을 끼치는 현상
회귀 분석 : 독립 변수와 종속 변수 사이 상관관계
-
2개 이상의 독립변수가 상관관계를 높게 가지고 있을 때 발생!
-
클러스터링 과정에서 특정 변수들이 -> 결과에 과도하게 영향 끼침!
- 두 변수가 거의 동일하다면 불필요한 중복 영향력
-
커머스 회사의 판매 데이터 분석
- 판매량, 광고 지출액, 마케팅 지출액
- 광고 지출액 - 마케팅 지출액 : 높은 상관관계 -> 이것이 다중공선성 예시!
- 모델이 중요도를 과대평가해서 판매량으로 예측하는 것들의 정확도 떨어짐!
- 다중공선성 문제의 해결?
- 두 변수 중 1개만 선택
- 두 변수 결합 -> 새로운 변수 생성
- 다중공선성 완화(상관관계를 떨어뜨리는 것)
- 다중공선성 문제의 가장 대표적인 해결 방법
- 주성분 분석(PCA) 같은 차원 축소 기술로 상관관계가 없는 변수 집합 생성
-
상관계수 시각화로 다중공선성 문제 살펴보기

- 가장 상관 관계가 높은 변수 조합은?
- 필자의 경우,
total_transactions와unique_products
- 필자의 경우,
- 높은 상관관계를 가지는 변수 쌍은?
- 0.90 이상 :
total_transactions와unique_products,user_total과item_cnt - 0.70 이상 :
purchase_cnt와item_cnt,purchase_cnt와user_total...
- 0.90 이상 :
- 가장 상관 관계가 높은 변수 조합은?
12-4. 피처(feature) 스케일링
피처 스케일링
- 독립변수 또는 feature(특징)들의 범위를 정규화
Feature Scaling을 해야 하는 이유
- 피처 스케일링과 K-Means 클러스터링
- 데이터 포인트 간
거리개념에 가장 크게 의존해 클러스터 형성 - 데이터 분포 -> 데이터간 거리가 가까우면 동일 클러스터!
- feature가 유사 척도를 사용하지 않으면..
- 값이 큰 feature가 클러스터링 결과에 불균형 발생시킴.
- 데이터 포인트 간
- 피처 스케일링과 차원 축소(주성분 분석:PCA)
- PCA : 차원 축소 종류 중 하나, 고차원 dataset에서 가장 중요한 feature를 추출해 데이터 차원을 줄이는 것!
- 다중공선성이 있는 컬럼을 제거 -> 나머지 칼럼으로 데이터 특성을 유지하며 차원 축소 -> 데이터 압축
- 차원 축소 이전 데이터 스케일링을 하는 것이 좋음.
피처 스케일링하기
- 각 특성 평균이 0, 표준 편차가 1이 되도록!
- 스케일링은 연속형 데이터만 진행(∵
CustomerID만 범주형)
- scikit-learn의 변수 스케일링 클래스
StandardScaler불러오기- StandardScaler : 스케일링의 한 방법, scaler 변수에 할당해 클래스 객체 생성

user_data에 스케일링 적용하기- copy()로 원본 데이터 훼손 방지 -> 복사본 데이터
data생성 - CustomerID 제외 컬럼명을 모아 스케일링 ->
scaler.fit_transform()scaler.fit_transform()
- fit(학습) : 데이터 구조 학습, 각 특성 평균 및 표준 편차 계산
- transform(변환) : 학습한 정보를 써서 데이터 변환, 각 특성 값을 평균으로 빼고 표준 편차로 나눔.
- copy()로 원본 데이터 훼손 방지 -> 복사본 데이터
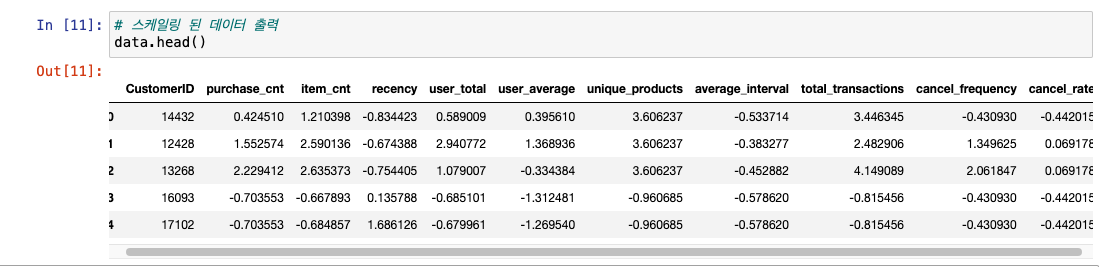
- 최종 스케일링 데이터 출력
- 기존 양수 -> 더 작아짐.
- 음수값도 생김!
- 각 컬럼 값 분포가 평균 0, 표준 편차가 1이 되도록 스케일링했으니!
이외의 스케일링 클래스
- MinMaxScaler
- 모든 값이 0과 1 사이 위치하도록 데이터 변환
- 특성 최솟값 0, 최대값 1로 설정 -> 사이 값들은 비례 조정
- 데이터 분포가 불균등할 때 사용
- 그림, 이미지 데이터 처리
- RobustScaler
- 데이터 중앙값(median) 및 사분위수(quartiles)를 통한 데이터 스케일링
- 이상치 영향을 덜 받아 이상치 데이터가 많은 경우 용이
- 각 특성 중앙값을 뺀 후, 1사분위수와 3사분위수 IQR(범위)로 나눔.
- Normalizer
- sample을 독립적으로 처리해 샘플 벡터 크기가 1이 되도록 함.
- 방향, 각도만 중요할 때 사용(길이는 중요하지 x)
- 텍스트 데이터, 다차원 시계열 데이터
12-5. 차원 축소(Dimensionality Reduction)
정의
- 다차원 데이터 차원을 축소해 -> 새로운 데이터 생성
차원 축소를 해야하는 이유는?
- 다중공선성 식별
- 중복 정보 제거 및 다중공선성 문제 완화 가능!
- K-Means 클러스터링으로 더 나은 클러스터링
- K-Means 클러스터링의 경우
거리기반 알고리즘이니 feature가 많으면 유의미한 기저 패턴의 희석 가능성 ⬆️ - 차원 축소를 통해 더 조밀하며 잘 구분되는 클러스터를 찾게 도와주는 것
- K-Means 클러스터링의 경우
- 노이즈 감소
- 가장 중요한 feature에만 초점을 맞춰 노이즈 제거
- 시각화 향상
- 차원 축소를 통해 데이터를 몇 개 주요 구성 요소로 축소해 쉬운 시각화
- 계산 효율성 향상
- feature 수를 줄여 계산 시간 단축 및 클러스터링 알고리즘의 효율적 사용
차원 축소 방법을 선택해보자.
- 종류 : PCA, ICA, ISOMAP, t-SNE, UMAP 등
- 선형 차원 축소 : PCA
- 비선형 차원 축소 : ISOMAP, LLE, t-SNE
- PCA(주성분 분석, Principal Component Analysis) 사용
- 데이터 내 선형 관계 포착에 용이
- 다중공선성 dataset에 강하기 때문!
- 주성분(Principal Component)?
- 차원 축소 : 고차원 데이터 주요 특징을 유지하는 동시에 차원만 줄이는 기술
- zip 파일 같은 경우!
- 몇 개 feature를 단순 제거하는 것이 아닌,
주성분이라는 새 변수가 생성됨(이 주성분이 원본 데이터 분산을 포착) - 각 주성분이 -> 데이터 전체 변동성의 어느정도를 설명하는지!
PCA 적용
- 라이브러리 불러오기 & CustomerID를 제외한 컬럼에 PCA 적용
data에 대해 학습한 PCA를 활용해explained_variance_ratio및 누적분포 계산explained_variance_ratio : 각 주성분이 데이터 분산을 얼마나 포착하는지에 대한 비율
- 결과 시각화

- 결과 분석
- 첫 번째 주성분 : 전체 분산의 44%
- 첫 2개 주성분 : 61%의 분산을 함께 설명
- 첫 3개 주성분 : 전체 분산의 73% 설명
- 최적 주성분 수 선택하기
- == 엘보우 포인트 찾기
- cumulative explained variance(누적 설명 분산)이 가장 작게 증가하는 지점을 찾는 것
- 5, 6번째 즈음부터 둔화(전체 분산의 95%)
- == 엘보우 포인트 찾기
처음 6개 주성분 유지로 데이터 차원 줄이기!
- CustomerID를 제외한 칼럼
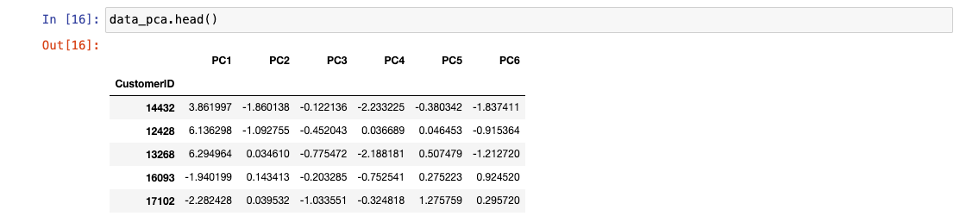
data를 압축해 6개 특성을 가진data_pca생성 & 최종 결과 출력
12-6. K-Means 클러스터링
-
K-Means
- 지정된 그룹 수인
K로 데이터를 클러스터링하는 비지도 학습 알고리즘 - 각 클러스터 평균(mean)으로 K개 클러스터로 묶는 방식
- 각 데이터 포인트를 가장 가까운 중심에 할당 -> 그 포인트의 평균을 계산 -> 중심을 업데이트(수렴 또는 원하는 조건에 도달할 때까지 반복)
- 지정된 그룹 수인
-
유의할 부분
- 각 실행마다 다른 레이블을 할당 가능
- 데이터 포인트의 선택 기준에 따라 다른 값이 나올 것!
- 그렇기 때문에, 각 클러스터의 샘플 빈도를 기반으로 레이블을 교환함.
클러스터의 샘플 빈도에 기반한 레이블의 교환
-
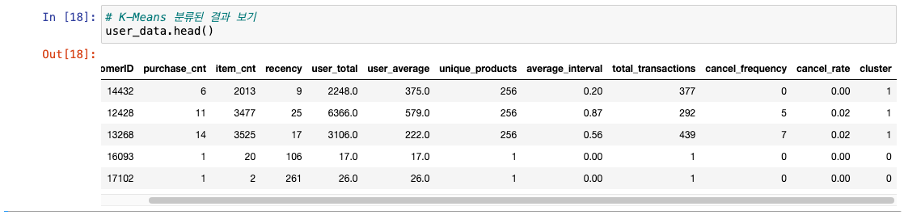
데이터에 K-Means 클러스터링 진행
a. 데이터 포인트는 임의 클러스터로 할당 -
각 클러스터에 속하는 데이터 포인트 개수 계산
-
가장 큰 클러스터(가장 많은 데이터 포인트)에 새로운 레이블 할당
a. 데이터 포인트 순서대로 정렬 :most_common() -
기존 클러스터링 결과에 새로운 레이블 매핑 적용 -> 레이블 할당에 일관성 부여(== 가장 큰 클러스터가 첫번째 그룸 0에 속하도록!)
- 각 클러스터별 고객 수 확인하기

12-7. 시각화 및 결과 분석
- 최상위 2개 PC(주성분) 선택 및 시각화
- 클러스터의 분리 및 응집 품질 시각화하여 확인!
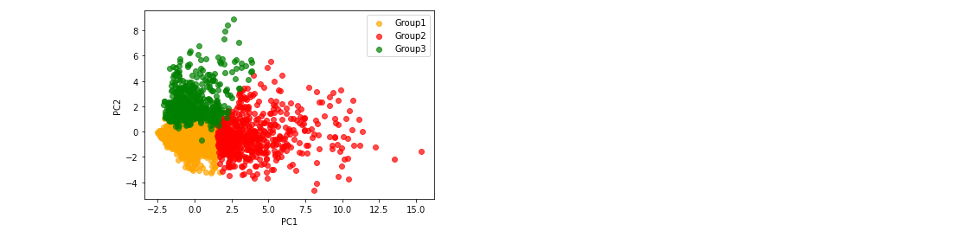
- 클러스터의 분리 및 응집 품질 시각화하여 확인!
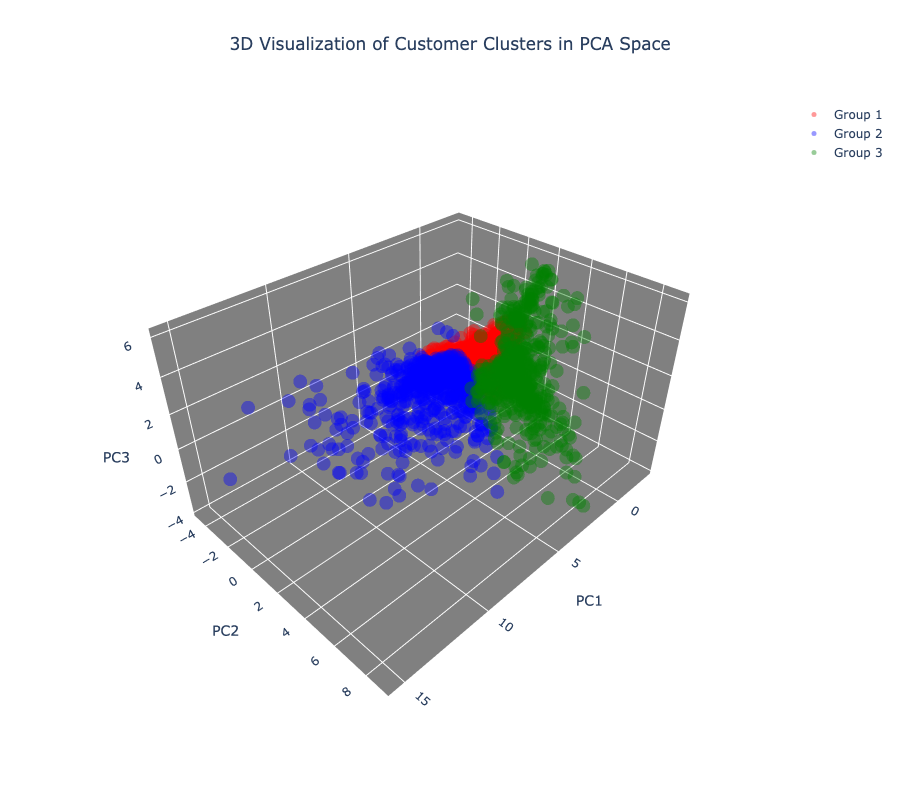
3D 시각화
-
위의 결과를 3D 시각화하기 위해
plotly사용!-
plotly설치
-
시각화
참고 : 이미지 고화질로 다운로드하려면 상단에서 해당 메뉴 이용하기


-
고객 세그먼테이션을 통한 인사이트와 전략
- RFM 총점에 따른 고객 세그먼테이션
- Recency, Frequency, Monetary가 각각 5점 -> 등급을 이용한 마케팅 전략을 세울 수 있음!
- 등급별 할인 혜택 및 마케팅 전략을 세울 수 있음.
- VVIP: 15점인 고객
- VIP: 12~14점인 고객
- 골드: 9~11점인 고객
...
- RFM 각 구성 요소 점수에 따른 고객 세그먼테이션
- R, F, M이 모두 만점이라면 -> VVIP로 지정
- R이 1, F와 M이 만점 -> 잠재 구매력이 높고 최근 구매가 없는 고객 -> 구매하면 "추가 할일"을 해주는 프로모션으로 구매 유도!
- RFM 분석과 K-Means 클러스터링을 사용한 고객 세그먼테이션
- RFM Score + 클러스터링(K-Means) 진행
- 다차원적, 세밀한 고객 세분화!
- K-Means 클러스터링으로 고객을 3개의 그룹으로 나누기
- 각 그룹 별 차이점을 추가 분석 -> 타겟 마케팅 전략 고려하기!
ex) 그룹 1의 purchease_cnt(구매 빈도), user_average(평균 구매금액) 평균이 타 그룹에 비해 높다 -> 그룹 1만의 마케팅 전략을 세우는 것
- 각 그룹 별 차이점을 추가 분석 -> 타겟 마케팅 전략 고려하기!
- 클러스터별로 group1, group2, group3 데이터 생성

- 각 그룹의 summary 정보 출력 :
describe()로 각 feature별 데이터 포인트 수 및 평균, 분산 등 정보 확인- group1


- group2

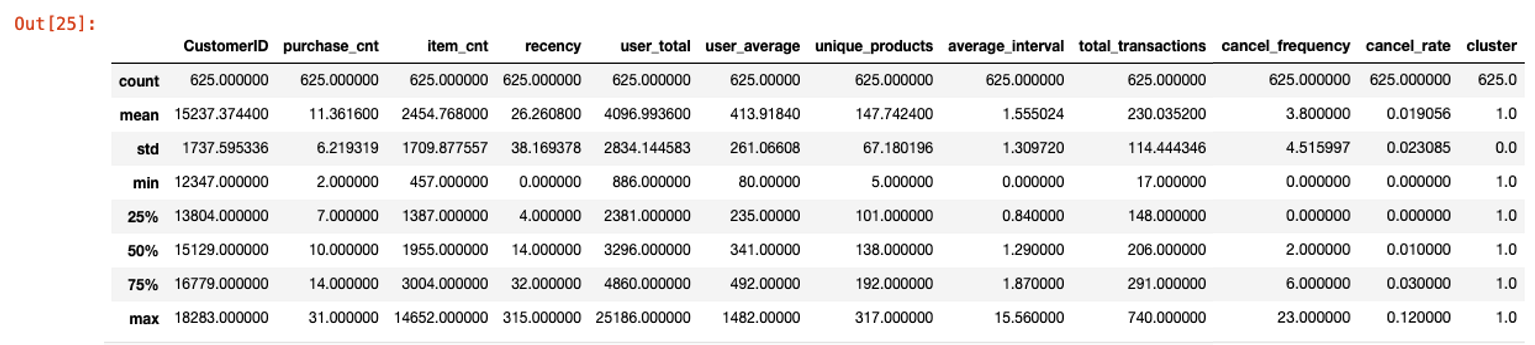
- group3

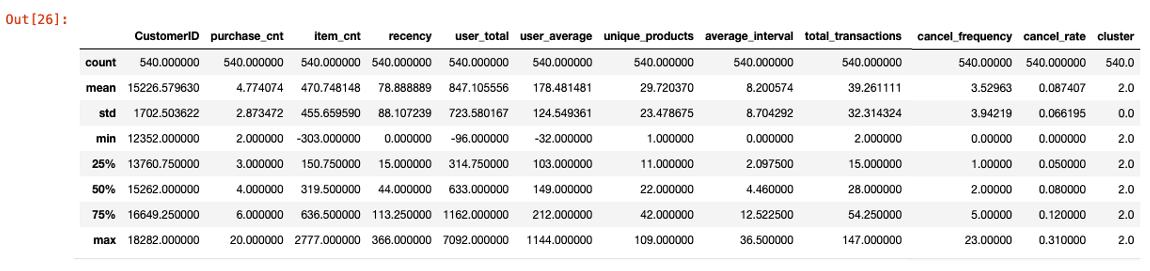
- group1
K-Means 클러스터링 방식의 강점
- 풍부한 데이터 사용
- RFM 요소와 더불어 더 다양하게 고객 속성 고려 가능
- 복잡한 고객 데이터 분석도 용이하게!
- 현업에서는 -> 많은 행동 데이터들을 3가지 기준에만 국한되어 계산하기 어려움.
- 즉, 여러 개의 feature들을 그래도 다 사용할 수 있음!
- 확장성
- 데이터를 그대로 사용함 -> 다양한 유형의 데이터 처리 가능
- 새 feature 추가 및 제거 -> 모델 재사용 가능
- 세밀한 세그멘테이션
- 세밀한 타겟 마케팅 전략 계획 및 효율성도 같이 높아짐.
- 숨겨진 패턴 분석
- 다양한 변수 안에 있는 고객의 행동 패턴 및 선호도를 서치 -> 단순 점수 계산보다 더 딥한 비즈니스 전략 및 인사이트를 제공!
결론
-
이하얀
-
시각화 결과
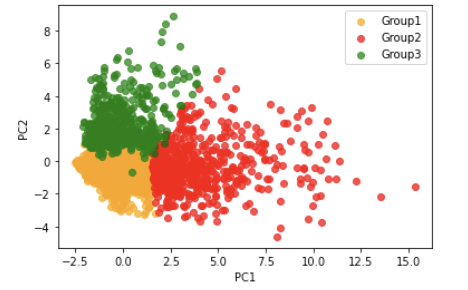
-
3D 시각화 결과
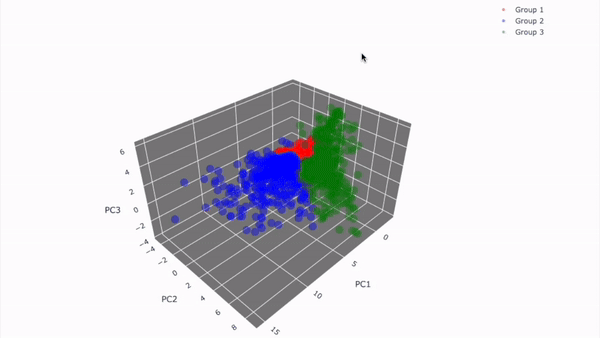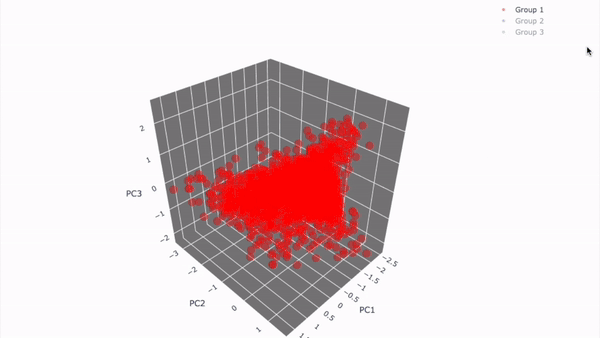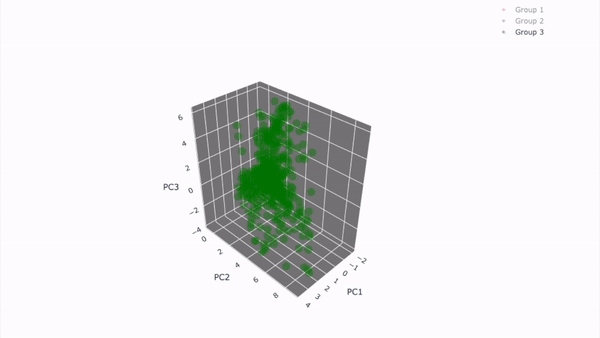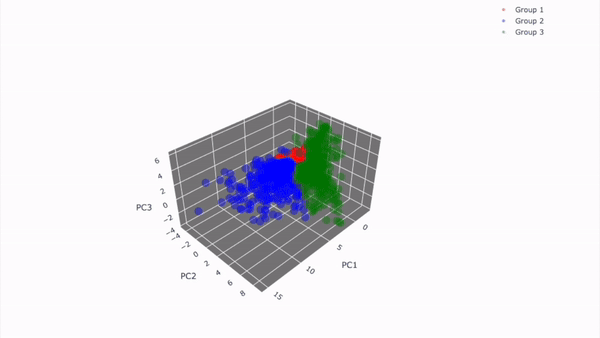
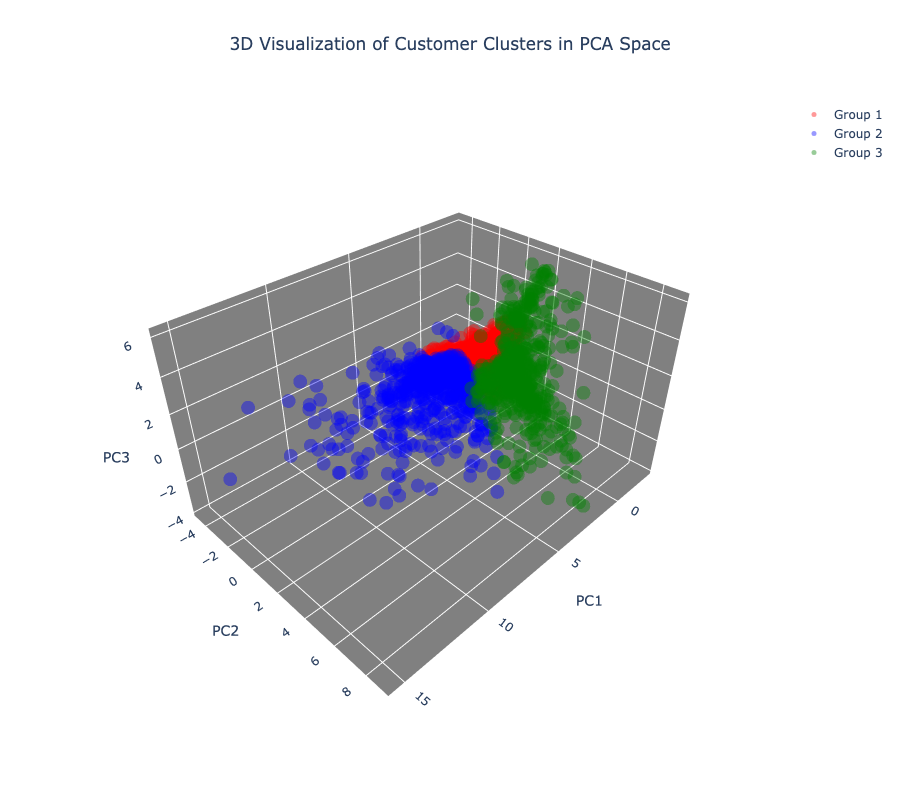
-
2D 시각화와 동일하게 뽑은 경우
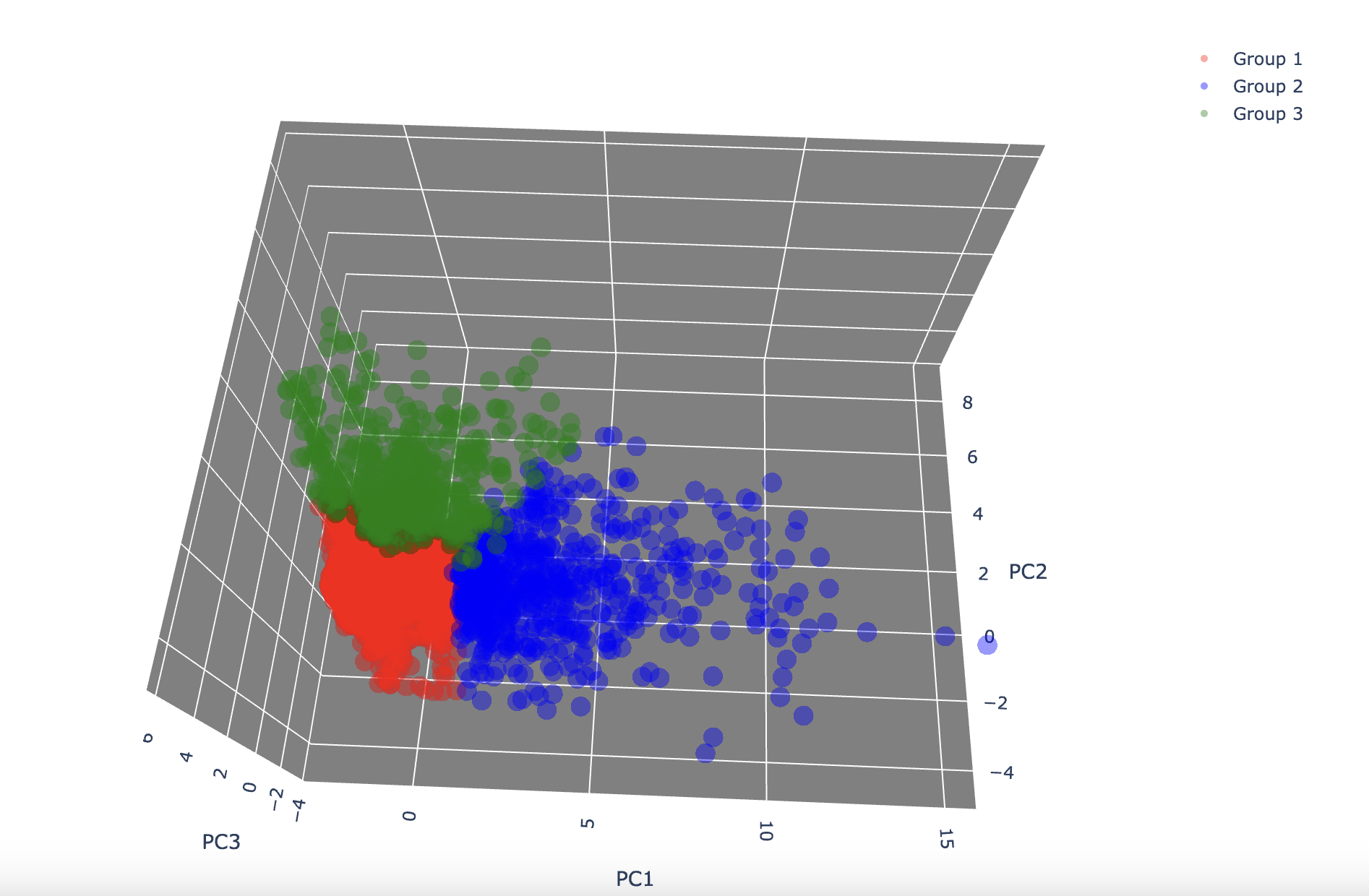
-
Group1
- 가장 큰 그룹으로 레이블을 드롭해줬기 때문에 사용자수가 직관적으로도 가장 많은 것을 확인할 수 있음.
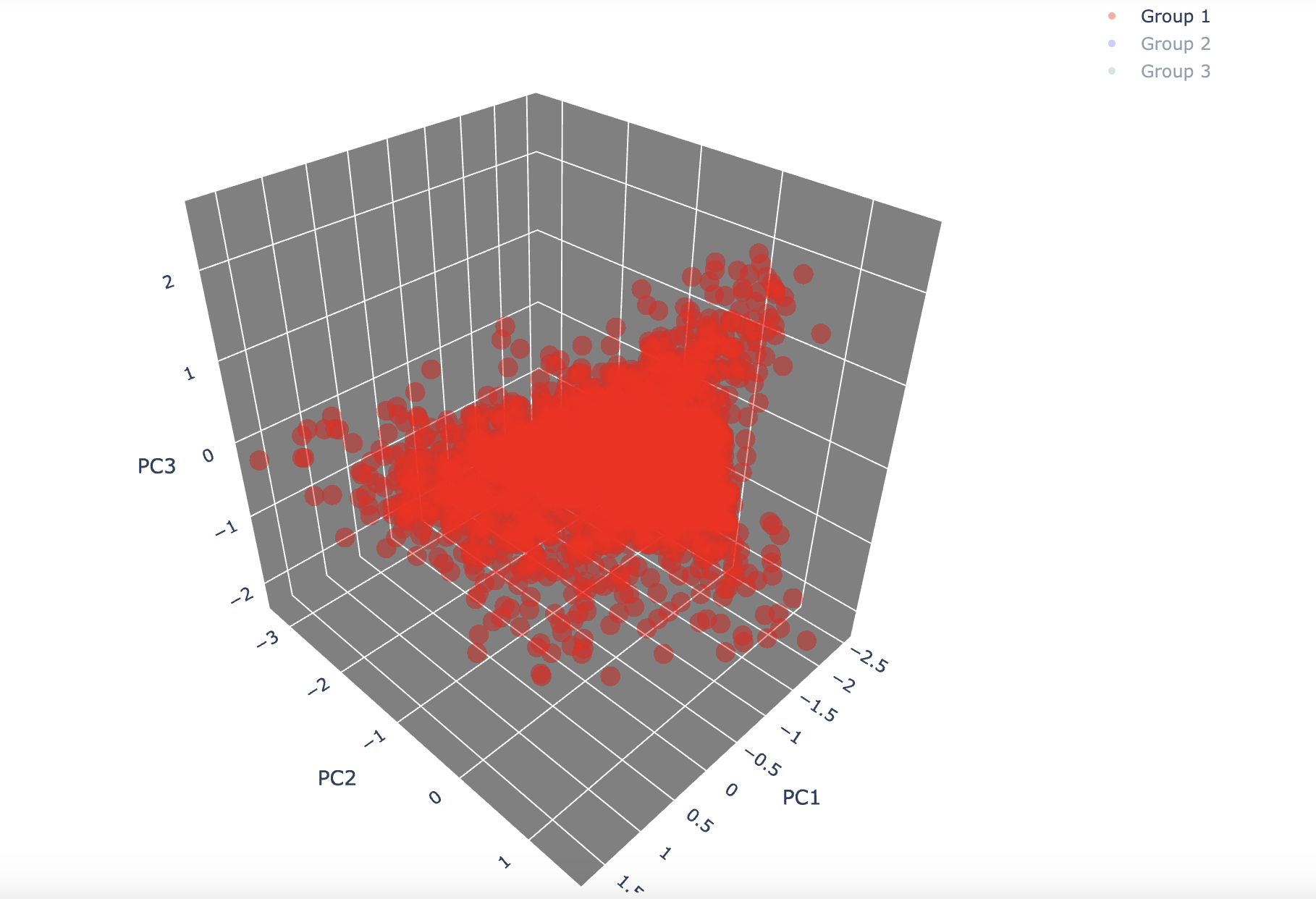
- 가장 큰 그룹으로 레이블을 드롭해줬기 때문에 사용자수가 직관적으로도 가장 많은 것을 확인할 수 있음.
-
Group2
- 클러스터링 이후 중앙값을 벗어나는 사용자가 가장 눈에 띄게 많은 그룹이 됨.
- 그룹2가 가장 넓은 범주의 기준을 가지고 있어 모두 포함하다보니 모든 값을 털어내지는 못한 것으로 보임.

-
Group3
- 전체적으로 그룹2와 유사하게 중앙값과 멀리 떨어진 값들이 보임.
- 가장 큰 특이사항은 그룹1과 명확히 겹치는 데이터가 존재한다는 것.
- 이 데이터의 경우 내용을 살펴 레이블을 변경해야할 가능성도 있어 보임.
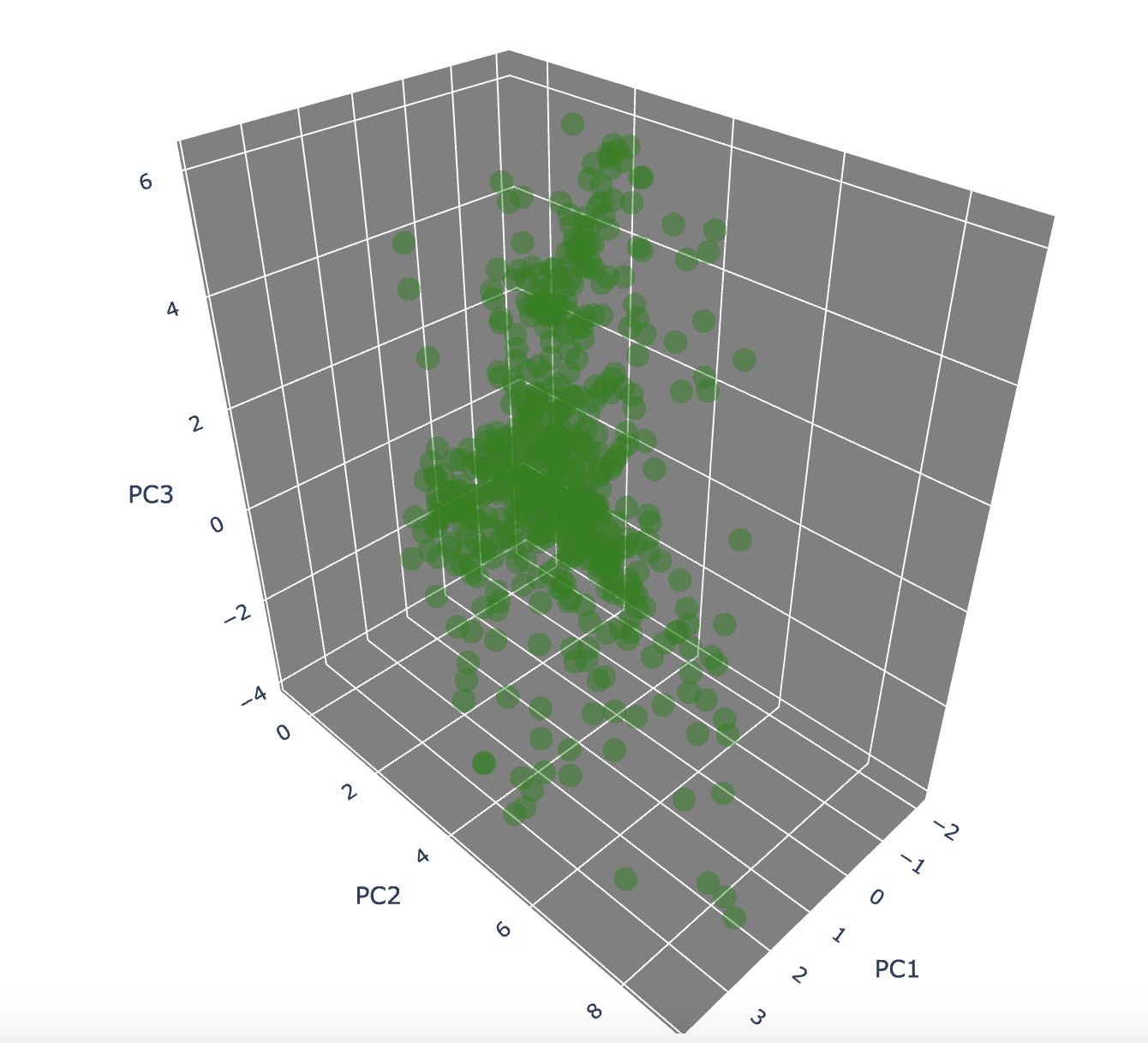
-
Group 1 + Group2
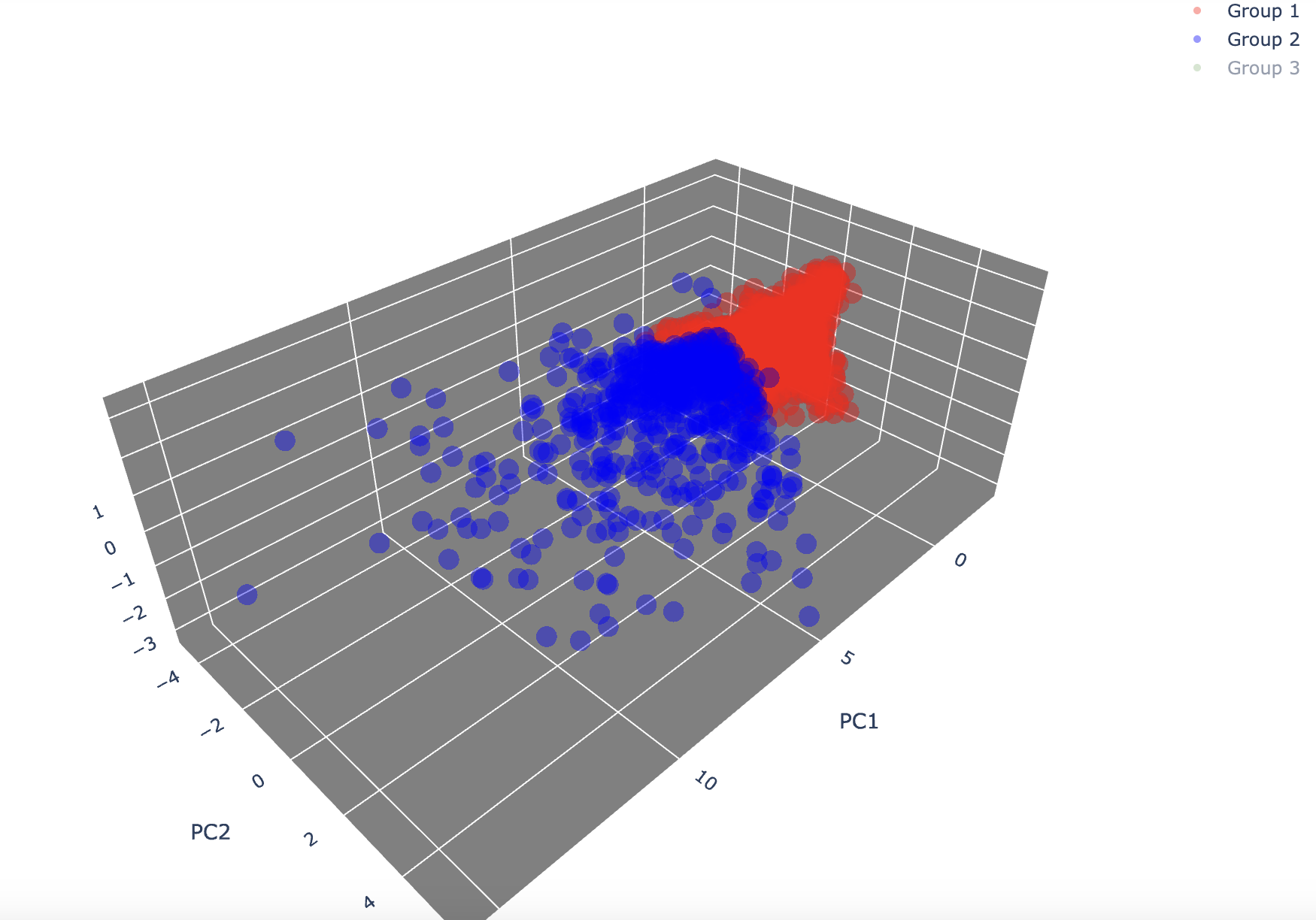
-
Group2 + Group3
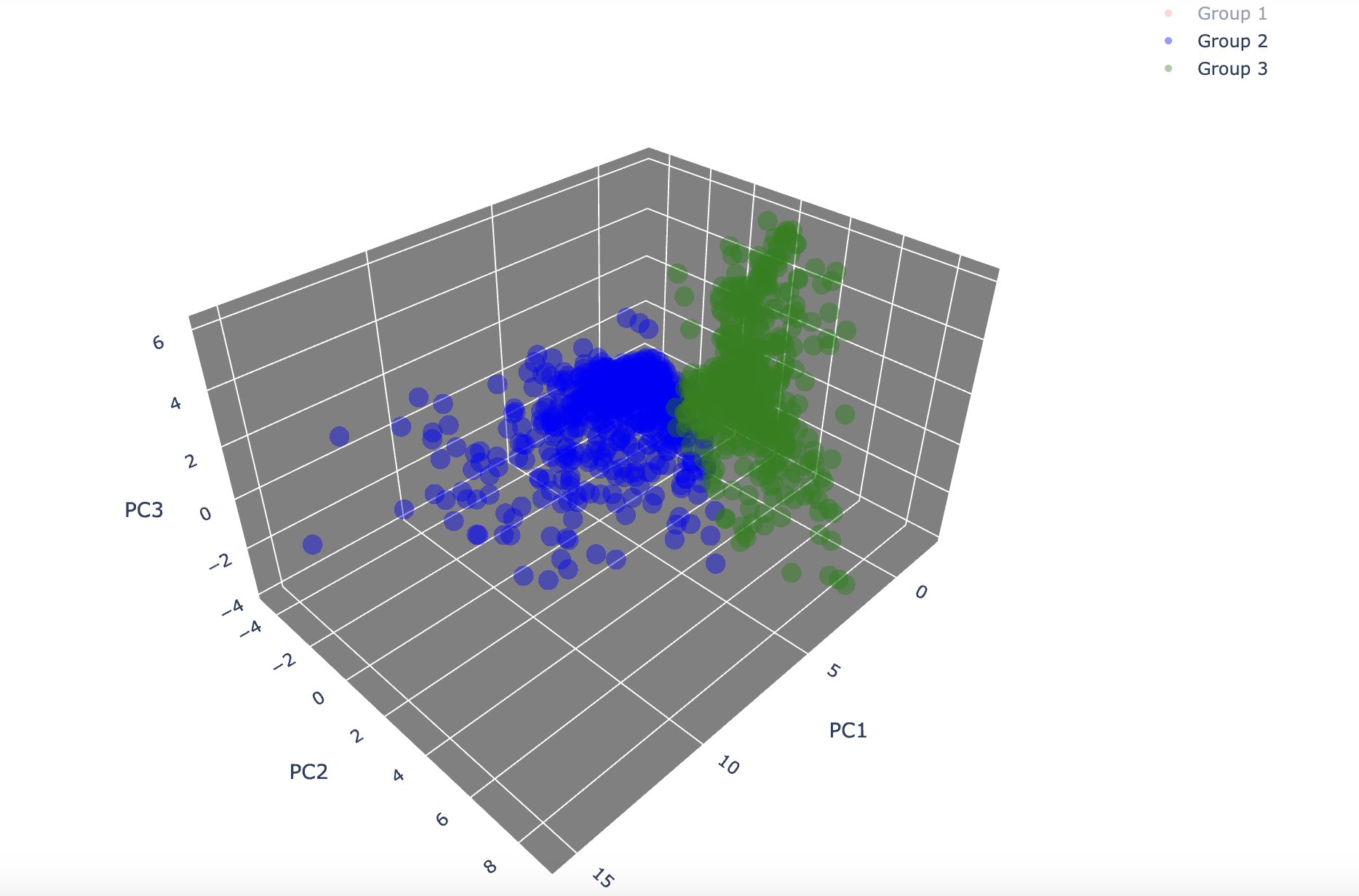
-
Group1 + Group3

- 한가지 견해
- 전반적으로 중앙값에 잘 몰린 결과가 나와 K-Means 알고리즘이 의도한 결과물에 가까운 시각화가 가능했음.
- 그룹1의 경우 스케일링과 클러스터링이 가장 잘 이루어진 그룹임을 알 수 있음.
- 데이터셋의 양이 많음과 동시에 좋은 질의 데이터인 경우 이렇게 의도한 결과가 잘 도출되는 경우가 많음.
- 그러나, 그룹2와 3의 경우 중앙값에서 넓게 퍼지는 형태를 공통적으로 띄고 있어, 레이블 값의 재설정이 필요해보임.
- 특히, 3D 시각화에서도 알 수 있듯 그룹3의 데이터가 그룹1의 데이터에 일부 포함되기 때문에 클러스터링을 다시 진행한다면 값의 경계를 변경하는 작업도 해볼 수 있겠다는 생각이 듦.
- 한가지 견해
-
-
-
- 만들어낸 데이터에 대해 각 회사 상황에 맞게 마케팅 전략을 고민하는 것까지 -> 데이터 분석가 및 데이터 사이언티스트의 업무 범위이다!