2021 부스트캠프 Day 21.
[Day 21] Graph
그래프란 무엇이고 왜 중요할까?
그래프란 무엇일까?
- 하나의 간선은 두 개의 정점을 연결한다.
- 모든 정점 쌍이 반드시 간선으로 직접 연결되는 것은 아니다.
- 그래프(Graph)는 정점 집합과 간선 집합으로 이루어진 수학적 구조
- 네트워크(Network)로도 불린다.
- 정점(Vertex)은 노드(Node)로 간선은 엣지(Edge) 혹은 링크(Link)로도 불린다.
그래프가 왜 중요할까?
-
우리 주변에는 많은 복잡계(Complex System)이 있다.
사회는 70억 인구로 구성된 복잡계이다.
통신 시스템은 전자 장치로 구성된 복잡계이다.
그 밖에도, 정보와 지식, 뇌, 신체 역시 복잡계로 생각할 수 있다. -
이런 복잡계가 가진 공통적인 특성은 무엇일까?
-> 구성 요소 간의 복잡한 상호작용이다. -
이런 복잡계를 어떻게 표현할까?
-> 정답은 그래프(Graph) 이다.
그래프는 복잡계를 표현하고 분석하기 위한 언어이다.
-
복잡계는 구성 요소들 간의 상호작용으로 이루어진다.
상호작용을 표현하기 위한 수단으로그래프가 널리 사용된다. -
복잡계를 이해하고, 복잡계에 대한 정확한 예측을 하기 위해서는
복잡계 이면에 있는 그래프에 대한 이해가 반드시 필요하다. -
그래프를 공부함으로써 복잡계가 등장하는 수많은 분야에 활용할 수 있다.
전산학, 물리학, 생물학, 화학, 사회과학 등이 그 예시이다.
그래프 관련 인공지능 문제
정점 분류(Node Classification) 문제
-
트위터에서의 공유(Retweet) 관계를 분석하여, 각 사용자의 정치적 성향을 알 수 있을까?
-
단백질의 상호작용을 분석하여 단백질의 역할을 알아낼 수 있을까?
연결 예측(Link Prediction) 문제
- 페이스북 소셜네트워크는 어떻게 진화할까?
추천(Recommendation) 문제
- 각자에게 필요한 물건은 무엇일까? 어떤 물건을 구매해야 만족도가 높을까?
군집 분석(Community Detection) 문제
- 연결 관계로부터 사회적 무리(Social Circle)을 찾아낼 수 있을까?
랭킹(Ranking) 및 정보 검색(Information Retrieval) 문제
- 웹(Web)이라는 거대한 그래프로부터 어떻게 중요한 웹페이지를 찾아낼 수 있을까?
정보 전파(Information Cascading) 및 바이럴 마케팅(Viral Marketing) 문제
- 정보는 네트워크를 통해 어떻게 전달될까? 어떻게 정보 전달을 최대화 할 수 있을까?
그래프 관련 필수 기초 개념
그래프의 유형 및 분류
-
방향이 없는 그래프(Undirected Graph) vs 방향이 있는 그래프(Directed Graph)
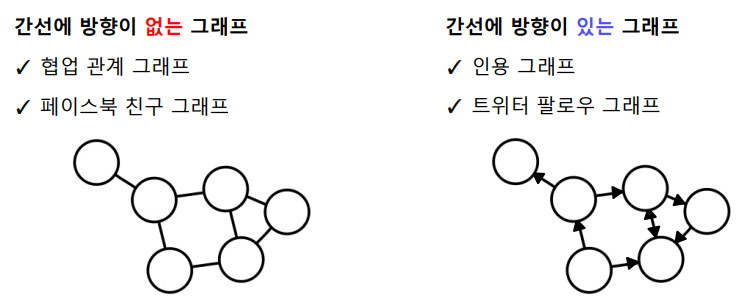
-
가중치가 없는 그래프(Unweighted Graph) vs 가중치가 있는 그래프(Weighted Graph)
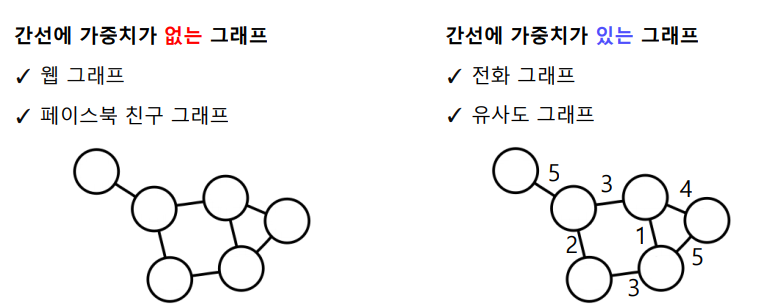
-
동종 그래프(Unpartitle Graph) vs 이종 그래프(Bipartite Graph)
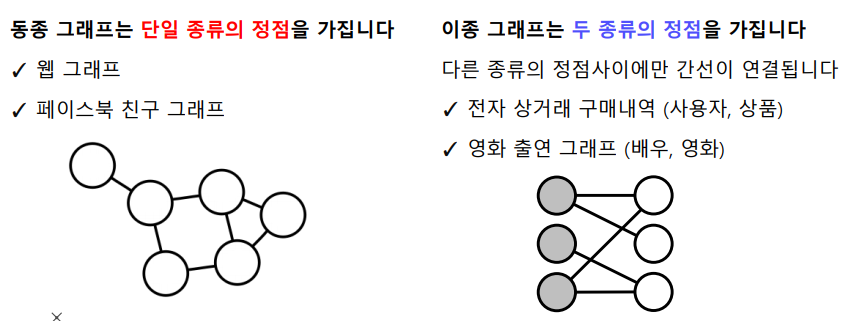
그래프 관련 필수 기초 개념
-
그래프(Graph)는 정점 집합과 간선 집합으로 이루어진 수학적 구조이다.
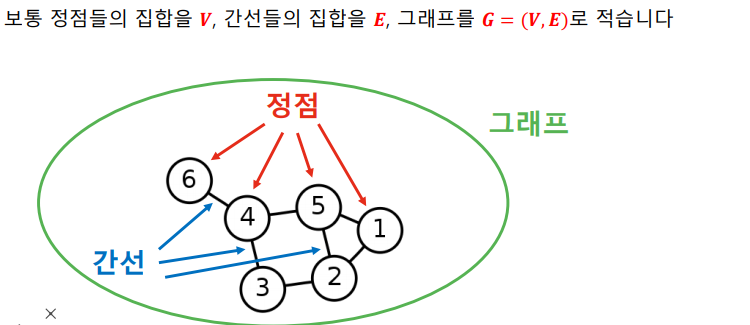
-
정점의 이웃(Neighbor)은 그 정점과 연결된 다른 정점을 의미한다.
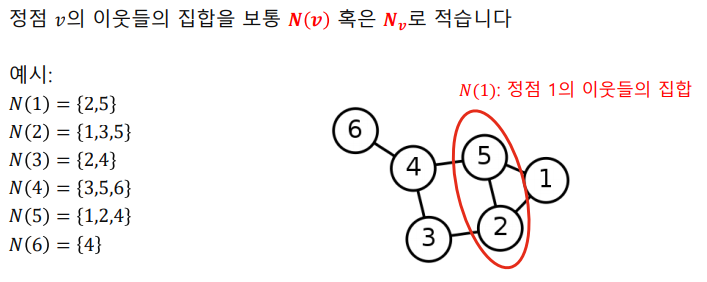
-
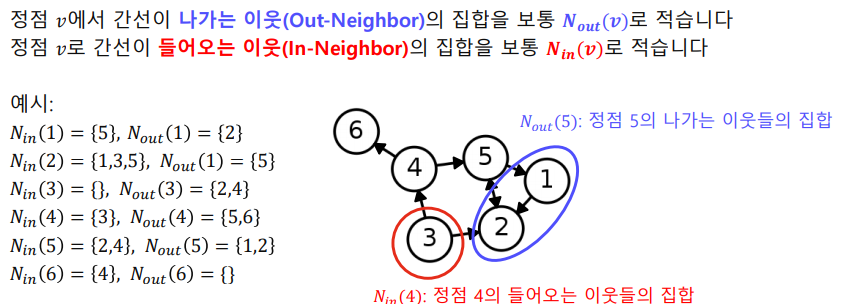
방향성이 있는 그래프에서는 나가는 이웃과 들어오는 이웃을 구분한다.
NetworkX
- NetworkX를 이용하여, 그래프를 생성, 변경, 시각화 할 수 있다.
- 구조와 변화 역시 살펴볼 수 있다.
import networkx as nx # NetworkX
import numpy as np # Numpy
import matplotlib.pyplot as plt
#그래프 초기화
print("#### Graph Init ####")
G = nx.Graph() # 방향성이 없는 그래프 초기화
DiGraph = nx.DiGraph() # 방향성이 있는 그래프 초기화
# 정점을 추가하고, 정점의 수를 세고, 목록을 반환
G.add_node(1) # 정점 1 추가
print("num of nodes in G : " + str(G.number_of_nodes())) # 정점의 수
print(str(G.nodes)) # 정점의 목록
# 간선을 추가
G.add_edge(1, 2) # 정점 1과 2사이에 간선 추가
print(str(G.edges))
#그래프 시각화
pos = nx.spring_layout(G) # 정점의 위치 결정
im = nx.draw_networkx_nodes(G, pos, node_color = "red", node_size = 100) # 색과 크기 지정
nx.draw_networkx_edges(G, pos) # 간선 출력
nx.draw_networkx_labels(G, pos, font_size=10, font_color="black)
plt.show()Save
간선 리스트(Edge List)
- 그래프를 간선들의 리스트로 저장
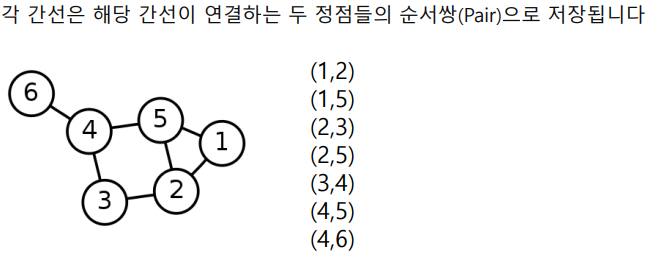
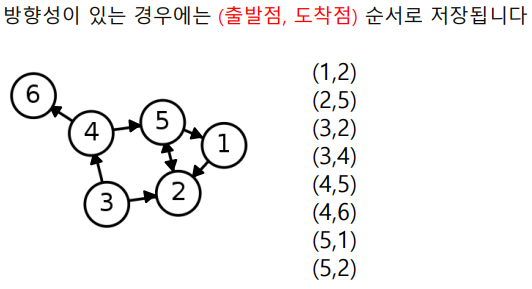
인접 리스트(Adjacent list)
-
방향성이 없는 경우
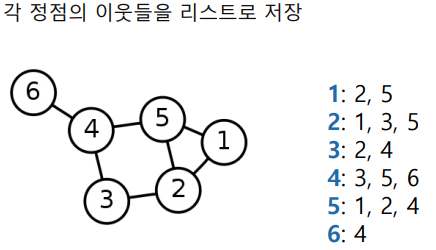
-
방향성이 있는 경우
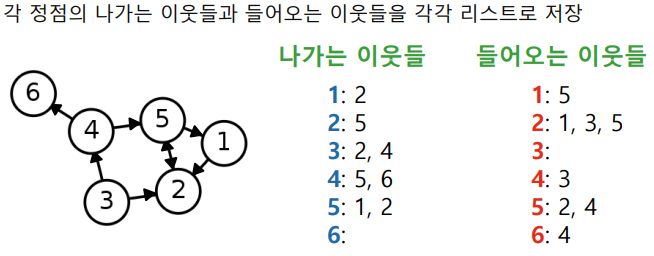
인접 행렬(Adjacency Matrix)
-
정점 수 X 정점 수 크기의 행렬
-
방향성이 없는 경우
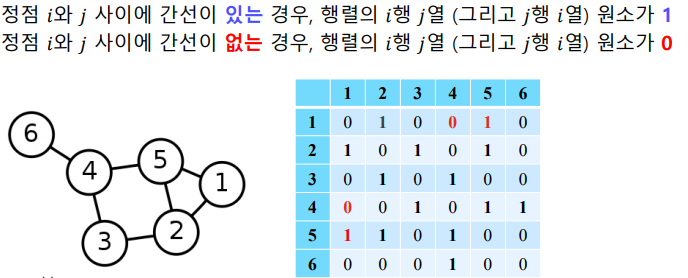
-
방향성이 있는 경우
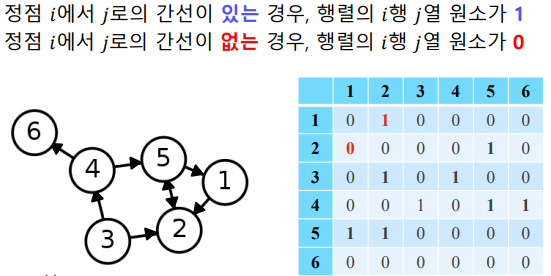
Code
# 그래프를 인접 리스트로 저장
nx.to_dict_of_lists(G)
# 그래프를 간선 리스트로 저장
nx.to_edgelist(G)
# 그래프를 인접 행렬(일반 행렬)로 저장
nx.to_numpy_array(G)
# 그래프를 인접 행렬(희소 행렬)로 저장
nx.to_scipy_sparse_matrix(G)
- 일반 행렬은 전체 원소를 저장하므로 정점 수의 제곱에 비례하는 저장 공간을 사용.
- 희소 행렬은 0이 아닌 원소만을 저장하므로 간선의 수에 비례하는 저장 공간을 사용
그래프를 이용한 기계학습 : 실제 그래프는 어떻게 생겼을까?
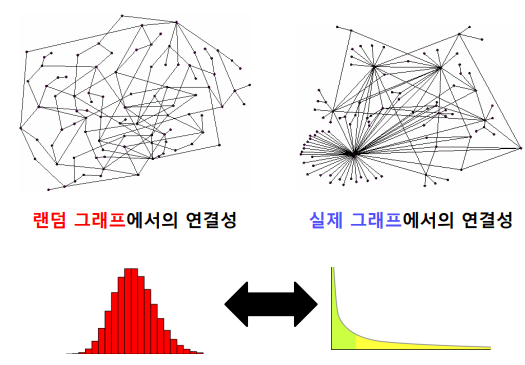
실제 그래프 vs 랜덤 그래프
- 랜덤 그래프(Random Graph)는 확률적 과정을 통해 생성한 그래프를 의미
- 에르되스와 레니가 제안한 랜덤 그래프 모델을 사용

에르되스-레니 랜덤 그래프(Erdos-Renyi Random Graph)
-
임의의 두 정점 사이에 간선이 존재하는지 여부는 동일한 확률 분포에 의해 결정
-
에르되스-레니 랜덤 그래프 는
- 개의 정점을 가진다.
- 임의의 두 개의 정점 사이에 간선이 존재할 확률은 이다.
- 정점 간의 연결은 서로 독립적(Independent)이다.
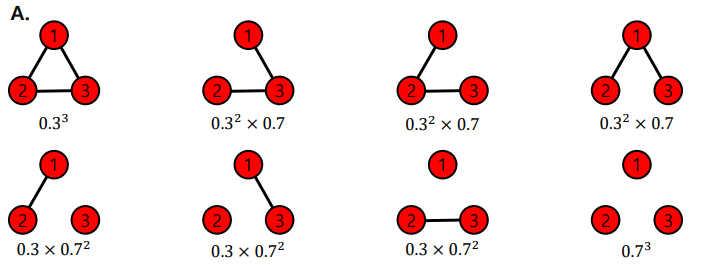
Ex. G(3, 0.3)에 의해 생성될 수 있는 그래프와 각각의 확률은?
작은 세상 효과
필수 개념 : 경로, 거리 및 지름
-
정점 와 사이의 경로(Path)는 아래 조건을 만족하는 정점들의 순열(Sequence)이다.
- 에서 시작해서 에서 끝나야 한다.
- 순열에서 연속된 정점은 간선으로 연결되어 있어야 한다.
-
경로의 길이는 해당 경로 상에 놓이는 간선의 수로 정의된다.
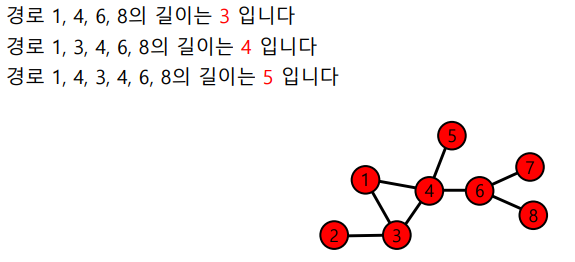
-
정점 와 의 사이의 거리(Distance)는 와 사이의 최단 경로의 길이이다.
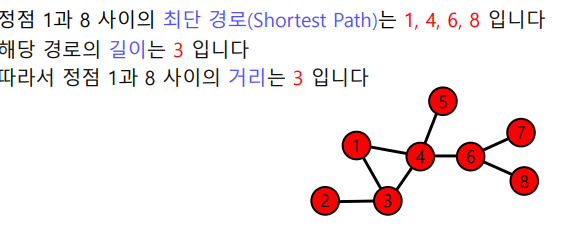
-
그래프의 지름(Diameter)은 정점 간 거리의 최댓값이다.
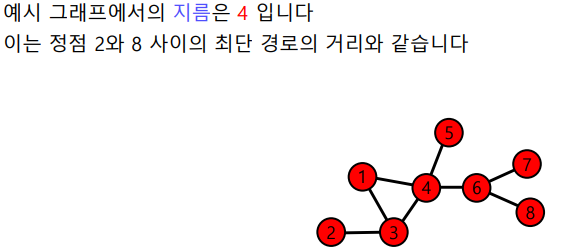
작은 세상 효과
-
임의의 두 사람을 골랐을 때, 몇 단계의 지인을 거쳐 연결되어 있을까?
-
여섯 단계 분리(Six Degrees of Separatation) 실험
- 사회학자 스탠리 밀그램(Stanley Milgram)에 의해 1960년대에 수행된 실험이다.
- 오마하 (네브리스카 주)와 위치타 (켄사스 주)에서 500명의 사람을 뽑았다.
- 그들에게 보스턴에 있는 한 사람에게 편지를 전달하게끔 하였다.
- 단, 지인을 통해서만 전달하게끔 하였다.
- 목적지에 도착하기까지 몇 단계의 지인을 거쳐 연결되어 있을까?
- 25%의 편지만 도착했지만, 평균적으로 6단계만을 거쳤다.
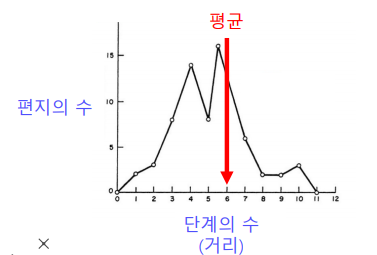
- 25%의 편지만 도착했지만, 평균적으로 6단계만을 거쳤다.
-
MSN 메신저 그래프에서는 어떨까?
- 정점간의 평균 거리는 7정도 밖에 되지 않는다.
단, 거대 연결 구조만 고려했다.
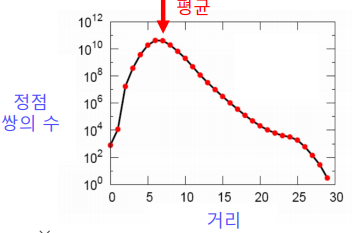
- 정점간의 평균 거리는 7정도 밖에 되지 않는다.
-
이러한 현상을 작은 세상 효과(Small-world Effect)라고 부른다.
- 한국에서는 "사돈의 팔촌"이 먼 관계를 나타내는 표현으로 사용된다.
즉, 아무리 먼 관계도 결국은 사돈의 팔촌(10촌 관계)이다.
- 한국에서는 "사돈의 팔촌"이 먼 관계를 나타내는 표현으로 사용된다.
-
작은 세상 효과는 높은 확률로 랜덤 그래프에도 존재한다.
- 모든 사람이 100명의 지인이 있다고 가정한다.
- 다섯 단계를 거치면 최대 100억(=1005)명의 사람과 연결될 수 있다.
- 단, 실제로는 지인의 중복 때문에 100억 명보다는 적은 사람일 것이다.
하지만 여전히 많은 사람과 연결될 가능성이 높다.
-
하지만 모든 그래프에서 작은 세상효과가 존재하는 것은 아니다.
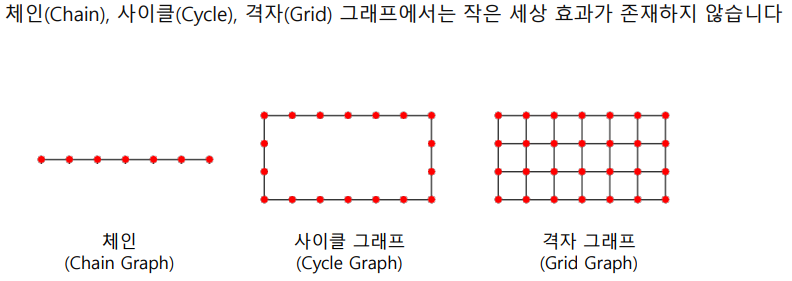
연결성의 두터운 꼬리 분포
필수개념 : 연결성
-
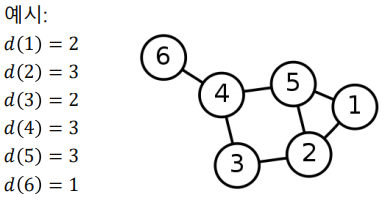
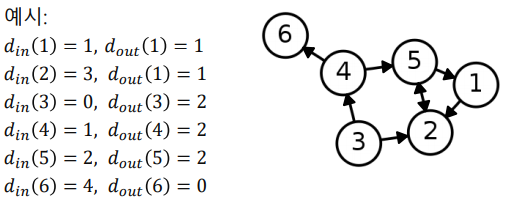
정점의 연결성(Degree)은 그 정점과 연결된 간선의 수를 의미한다.
-
정점 의 연결성은 해당 정점의 이웃들의 수와 같다.
보통 정점 의 연결성은 v 혹은 로 적는다.
-
정점의 나가는 연결성(Out Degree)은 그 정점에서 나가는 간선의 수를 의미
-
정점의 들어오는 연결성(In Degree)은 그 정점으로 들어오는 간선의 수를 의미
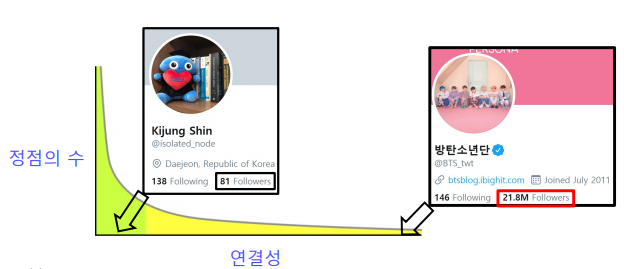
연결성의 두터운 꼬리 분포
-
실제 그래프의 연결성 분포는 두터운 꼬리(Heavy Tail)을 갖는다.
-
즉, 연결성이 매우 높은 허브(Hub) 정점이 존재함을 의미
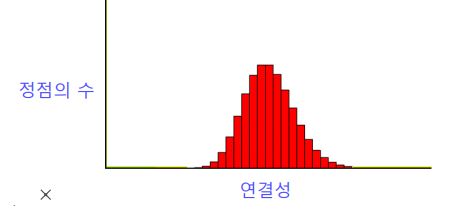
-
랜덤 그래프의 연결성 분포는 높은 확률로 정규분포와 유사
- 이 경우, 연결성이 매우 높은 허브(Hub) 정점이 존재할 가능성은 0에 가깝다.
- 정규분포와 유사한 예시로는 키의 분포가 있다.
키가 10미터를 넘는 극단적인 예외는 존재하지 않는다.
거대 연결 요소
필수 개념 : 연결 요소
- 연결 요소(Connected Component)는 다음 조건들을 만족하는 정점들의 집합을 의미
- 연결 요소에 속하는 정점들은 경로로 연결될 수 있다.
- 위 조건을 만족하면서 정점을 추가할 수 없다.
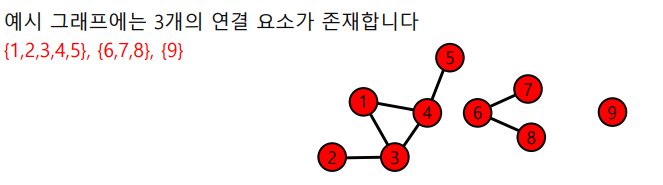
- 위 예시에서 {1,2,3,4}는 두번째 조건을 위배
- {6,7,8,9}는 첫번째 조건을 위배
거대 연결 요소
-
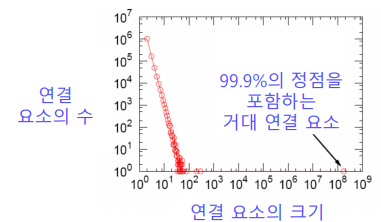
실제 그래프에는 거대 연결 요소(Giant Connected Component)가 존재
거대 연결 요소는 대다수의 정점을 포함 -
MSN 메신저 그래프에는 99.9%의 정점이 하나의 거대 연결 요소에 포함
-
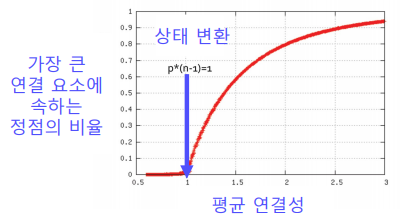
랜덤 그래프에도 높은 확률로 거대 연결 요소(Giant Connected Component)가 존재한다.
- 단, 정점들의 평균 연결성이 1보다 충분히 커야 한다.
- 자세한 이유는 Random Graph Theory를 참고
군집 구조
필수 개념 : 군집
-
군집(Community)이란 다음 조건들을 만족하는 정점들의 집합니다.
- 집합에 속하는 정점 사이에는 많은 간선이 존재한다.
- 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재한다.
-
수학적으로 엄밀한 정의는 아니다.
지역적 군집 계수
-
지역적 군집 계수(Local Clustering Coefficient)는 한 정점에서 군집의 형성 정도를 측정.
-
정점 의 지역적 군집 계수는 정점 의 이웃 쌍 중 간선으로 직접 연결된 것의 비율을 의미
-
정점 의 지역적 군집 계수를 로 표현

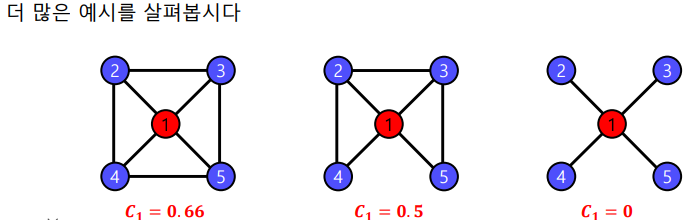
-
연결성이 0인 정점에서는 지역적 군집게수가 정의되지 않는다.
-
지역적 군집계수가 군집이랑 어떻게 연결되는 것일까?
- 정점 의 지역적 군집 계수가 매우 높다고 가정할 때,
정점 의 이웃들도 높은 확률로 서로 간선으로 연결되어 있다.
정점 와 그 이웃들은 높은 확률로 군집을 형성한다.
- 정점 의 지역적 군집 계수가 매우 높다고 가정할 때,
전역 군집 계수
-
전역 군집 계수(Global Clustering Coefficient)는 전체 그래프에서 군집의 형성 정도를 측정
-
그래프 의 전역 군집 계수는 각 정점에서의 지역적 군집 계수의 평균이다.
단, 지역적 군집계수가 정의되지 않은 정점은 제외한다.
높은 군집 계수
-
실제 그래프에서는 군집 계수가 높다. 즉 많은 군집이 존재한다.
-
동질성(Homophily)
- 서로 유사한 정점끼리 간선으로 연결될 가능성이 높다.
- 같은 동네에 사는 같은 나이의 아이들이 친구가 되는 경우가 그 예시이다.

-
전이성(Transitivity)
- 공통 이웃이 있는 경우, 공통 이웃이 매개 역할을 해줄 수 있다.
- 친구를 서로에게 소개해주는 경우가 그 예시이다.
-
랜덤 그래프에서는 지역적 혹은 전역 군집 계수가 높지 않다.
- 구체적으로 랜덤 그래프 에서의 군집 계수는 이다.
랜덤 그래프에서의 간선 연결이 독립적인 것을 고려하면 당연한 결과이다.
즉 공통 이웃의 존재 여부가 간선 연결 확률에 영향을 미치지 않는다.
- 구체적으로 랜덤 그래프 에서의 군집 계수는 이다.
