
이진 탐색(Binary Search)
말 그대로 탐색에 대한 알고리즘 중 하나로 이진 탐색은 정렬된 상태의 데이터에서 특정 값을 빠르게 탐색하는 방법이다.
그렇다면 어떻게 찾는 것일까?
1. 찾고자 하는 값과 데이터 중앙에 있는 값을 비교
2. 찾고자 하는 값이 더 작으면 데이터 왼쪽 부분에서 이진탐색
3. 찾고자 하는 값이 더 크면 데이터 오른쪽 부분에서 이진 탐색
생생각보다 간단할 수 있지만 이를 응용이 하게 된다면 상당히 어려운 알고리즘이란 것을 알 수 있다. 그렇기에 기본적인 예시를 하나 더 들어 보도록 하겠다.
이진 탐색 예시
오른 차순으로 정렬된 데이터가 있다고 가정하자.
{12 , 13 ,14 ,45, 78, 99}이러한 데이터를 바탕으로 13라는 데이터를 찾아보겠다.
- 첫 번째 시도
해당 값에 대한 가운 데 값을 찾아야 한다.
여기서 가운데 값은 문제별로 정의하는것이 다양하겠지만 우리는 해당 배열의 값중에 값을 찾는 방법이기에 arr의 범위를 사용해야한다.
그렇다면0 + arr.length / 2를 의미하게 되고 이 가운데 MID를 통해서 탐색을 시도 한다. arr에서 mid 의값은 45가 되게 된다.
45 > 13 13은 45보다 크므로 right의 인덱스를 범위를 좀 더 좁혀줘야 한다.right = mid - 1;로 수정을 한뒤 값을 찾아줘야 한다.
- 두 번째 시도
그렇다면 인덱스의 범위는 0부터 2까지의 범위 중에서 찾게 되는데 여기서 다시 MID 값을 찾고 계속해서 원하는 값을 찾는다면 범위는 좁혀오게 된다. 그렇게 만약 범위의 값을 찾는다면 break을 하고 검색을 종료하게 된다.
- 종료 조건
해당 사이클이 반복되면서 원하는 값을 찾았을 경우 사이클은 종료가 된다. 반면 찾지 못할 경우가 있다. 그럴 경우 없는 경우에는 left <= right 해당 조건문을 통해서 쉽게 탈출 조건을 추가해서 주면 된다. 생각을 해보자. 계속해서 찾다가 원하는 값을 못 찾고 있다면 해당 left right는 줄어들거나 증가하거나를 반복할 것이다. 그렇다면 left < right를 성립이 불가능하게 되면서 사이클은 종료가 될 것이다.
⚠️주의 사항⚠️
위 사이클을 어느정도 보시고 나서는 감이 오겠지만 반드시 정렬된 상태여야만 가능한 조건이다.
시간 복잡도 --> O(longN)
파라메트릭 서치(Parametric Search)
그리고 하나 더 말씀을 드리고 싶은 이진 탐색 종류가 있다. 바로 파라 메트릭 서치인데요! 여기서 파라 메트릭 서치란? 최적화 문제를 결정 문제(예 또는 아니요.)로 바꾸어 해결하는 기법이다.
❗❗대표적으로 원하는 조건을 만족하는 가장 알맞은 값을 찾는 문제에서 주로 사용된다.❗❗
📌예시를 하더 들어보자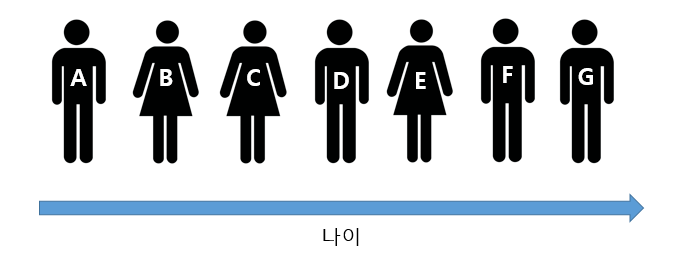
열 명의 사람이 있다고 가정합니다. 열 명의 사람을 나이순으로 정렬이 되어 있고 해당 사람들은 운동을 좋아하는 보디빌더들이라고 가정합니다. 하지만 보디빌더들은 몸을 키우기 위해서는 기록까지가 운동이라고 생각합니다. 그렇기에 매일매일 자기가 먹은 음식들을 기록합니다. 운동을 기록하기 시작한 보디빌더들의 나이는 30살 이상이라면 그분들은 이미 식단을 기록하는 습관을 지니고 있습니다. 그렇다면 위 10명의 사람 중 식단을 기록하는 사람 중 최소의 나이를 구하시오.
이러한 문제가 바로 파라메트릭 서치의 표본이 됩니다.
최적화 문제 : 식단을 기록하는 습관을 가진 최소 나이를 가진사람
식단을 기록하는가? : 네 or 아니오
그렇다면 식단을 하는지 안 하는지 라고 묻는 것은 누구에게 하는 게 가장 현명할까요? 바로 나이가 많은 보디빌더들에게 하면 된다. 그래서 처음에 mid 값에서 식단을 하는지 묻고 그 해당하는 질문에 '아니오'를 내뱉는다면 점차 left의 값을 증가(mid + 1)시키면서 최소의 나이를 줄여나가면 되는 방식이다.
이러한 흐름은 매우 이분 탐색과 매우 흡사합니다. 그렇기에 파라 메트릭 서치는 의외의 문제들에 적용돼서 최적화 문제들을 조금 더 쉽게 풀 수 있게 해줍니다.
파라메트릭 서치의 핵심
- 결정문제라는 점
해당 값이 정답이 될 수 있는 값인지 아닌지를 쉽게 판단할 수 있어야 하며 이는 파라메트릭 서치로 풀 수 있습니다.
- 정답들의 배열이 연속적이어야 한다.
예를들어 어떤 조건에 만족하는 최솟값을 구하는 최적화 문제가 있다면 해당 값들은 기본적으로 연속적인 값을 조건으로 해야한다. 정답을 X라고 가정했을 때 X이하의 배열의 원소들은 모두 만족하거나 X 이상의 배열의 원소들은 모두 만족하는 것을 의미합니다.
마치면서
이진 탐색은 나에겐 처음에 갈피를 못 잡는 문제였다. (물론 지금도 그러하다..ㅠ) 하지만 이진 탐색을 다가가고자 정리를 통해서 접근했으며 아직은 명확하게 내가 이진 탐색 안다고는 말씀을 못 드리지만 그래도 한 걸음 더 다가갔다고 생각한다. 그리고 나는 처음에 파라 메트릭 서치란 것이 있는지도 몰랐고, 이게 이진 탐색의 하나의 종류라는 것도 몰랐다 하지만 이번에 정리를 통해서 알게 되면서 다음에 이러한 유형의 문제를 만난다면 이진 탐색으로 풀어야겠다는 생각을 명확하게 하고 가서 천만다행이라고 생각한다.
자료 제공
https://cjh5414.github.io/binary-search/
https://velog.io/@bbirong/5-1.-%EC%9D%B4%EC%A7%84%ED%83%90%EC%83%89-%EA%B0%9C%EB%85%90-%EC%8B%A4%EC%A0%84-%EB%AC%B8%EC%A0%9C
https://sarah950716.tistory.com/16
