경작 8일차 dfs, bfs

#230204 토 ~ #230205 일

오늘은 알고리즘 스터디 3일차(0202 목)에서 못 풀었던 dfs, bfs 구현을 해결했다.

문제를 푸는 방법은 두 가지이다 (사실 세 가지인데 스택 dfs는 내가 잘 몰라서 그렇게는 안 풀었다)

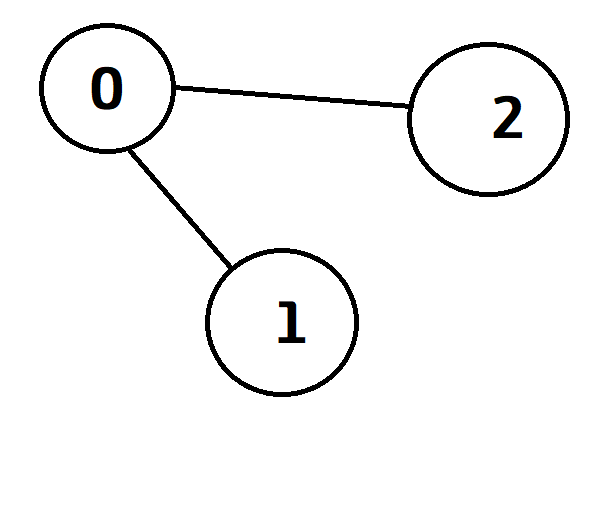
1. 인접 리스트로 구현하기 : 인접 리스트는 어떤 정점과 연결되어있는 정점들을 리스트에 넣어 연결된 두 정점을 표현하는 것이다. 다음과 같은 무방향 그래프가 있다면,
   
   인접 리스트는 아래와 같다 :

[
	[1,2],    // 0과 인접하는 정점 1, 2
	[0],      // 1과 인접하는 정점 0
	[0]       // 2와 인접하는 정점 1
    		]

2. 인접 행렬로 구현하기 : 인접 행렬은 두 정점 사이에 간선이 있는지 없는지를 행렬에 표현한 것이다. 두 정점이 연결되어있으면 간선이 있으므로 1, 연결되어있지 않으면 0으로 표현된다.
   위 그래프를 표현한 인접 행렬 A는 아래와 같다:

A = { 0 1 1
      1 0 0
      1 0 0 }

1. 백준 1260번 DFS와 BFS

---

<문제>
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

<입력>
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

<출력>
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.

---

1) 인접 리스트

처음에는 인접 리스트로 풀었다. vector 없이 풀고 싶어서 2차원 배열로 풀다가 한계에 도달해서 결국 vector를 쓰기로 했다. 그 와중에 vector도 쓸 줄 몰라서 vector로 2차원 배열 만드는 방법만 거의 30-40분을 찾아본 것 같다.. 실화냐 진짜 할 줄 아는 게 하나도 없어ㅎ

알고리즘 스터디 하다보면 몇몇 선배님들께서 파이썬 combination 함수 정말 편하다고 파이썬으로 넘어오라고 영업하시는데 사실 난 파이썬으로 넘어가고 싶어도 파이썬도 잘 모르고 파이썬 라이브러리도 하나~도 쓸 줄 모른다. 넘어가고 싶어도 못 넘어가요.. 저 진짜 이렇게 살아도 개발자 될 수 있을까요..? 파이썬은 잘 모르고 c++은 더럽게 못하는 나의 괴상한 수준.. 하염없이 눈물만 나는 하루였다 (그렇다고 진짜 운 건 아닙니다)

더 큰 문제는 파이썬이냐 아니냐가 아니라 풀긴 풀었는데 '틀렸습니다!!'라고 떴다는 것이다.. 비스에서 예제 입력은 잘 돌아갔는데 채점 결과가 틀린 걸 보니 내가 뭔가 잘못한 것 같다.. 근데 풀 만큼 풀어서 너무 지쳤기 때문에 그냥 써본 것에 의의를 두기로 했다. (대신 인접 행렬로 푼 건 맞았다)

인접 리스트 내 코드:

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
vector <int> graph[1001];
vector <int> vapex;
bool visited[1001] = { false, };
bool visited2[1001] = { false, };

void dfs(int a) {
    queue<int>q;
    visited[a] = true;
    cout << a << ' ';
    for (int i = 0;i < graph[a].size();i++) {
        if (!visited[graph[a][i]]) dfs(graph[a][i]);
    }
}

void bfs(int a) {
    queue<int>q;
    visited2[a] = true;
    q.push(a);
    while (!q.empty()) {
        int b = q.front();
        q.pop();
        cout << b << ' ';
        for (int i = 0; i < graph[b].size();i++) {
            if (!visited2[graph[b][i]]) {
                visited2[graph[b][i]] = true;
                q.push(graph[b][i]);
            }
        }
    }
}

int main() {
    int n, m, s;
    cin >> n >> m >> s;

    for (int i = 0;i < m;i++) {
        int apex, apex2;
        cin >> apex >> apex2;
        graph[apex].push_back(apex2);
        graph[apex2].push_back(apex);
    }


    for (int i = 0;i < n;i++) {
        for (int k = 0;k < graph[i].size();k++) {
            for (int j = k + 1;j < graph[i].size();j++) {
                if (graph[i][k] > graph[i][j]) {
                    int a = graph[i][k];
                    graph[i][k] = graph[i][j];
                    graph[i][j] = a;
                }
            }
        }
    }


    dfs(s);

    cout << '\n';


    bfs(s);
}

2) 인접 행렬

인접 행렬로 푸니까 정말 간단했다. 방문할 수 있는 정점이 여러 개일 때 노드값이 가장 작은 정점부터 방문한다는 조건을 충족하려면 인접 리스트로 풀 땐 리스트를 오름차순으로 정렬해야 해서 3중 중첩문을 써야했는데, 인접 행렬은 정렬이 필요없기 때문이다. 그래서 코드가 훨씬 짧아졌다.

#include <iostream>
#include <queue>          
using namespace std;                                                             
int graph[1001][1001]; ;
bool visited[1001] = { false, };                          
bool visited2[1001] = { false, };
int n, m, s;                            

void dfs(int a) {
    visited[a] = true;
    cout << a << ' ';
    for (int i = 1;i <= n;i++) {
        if (graph[a][i] == 1 && !visited[i]) dfs(i);
    }
}

void bfs(int a) {
    queue<int>q;
    visited2[a] = true;
    q.push(a);
    while (!q.empty()) {
        int b = q.front();
        q.pop();
        cout << b << ' ';
        for (int i = 1; i <= n;i++) {
            if (!visited2[i] && graph[b][i] == 1) {
                visited2[i] = true;
                q.push(i);
            }
        }
    }
}


int main() {
    cin >> n >> m >> s;

    for (int i = 0;i < m;i++) {
        int apex, apex2;
        cin >> apex >> apex2;
        graph[apex][apex2] = 1;
        graph[apex2][apex] = 1;
    }

    dfs(s);

    cout << '\n';
 
    bfs(s);
}

하여튼 풀어서 다행이다. 토요일에 다 푸려고 했는데 오늘(일요일)까지 넘어와버렸다. 오늘 해결 못했으면 진짜 내 컴퓨터를 죽였을 지도 모른다.. (컴퓨터는 잘못이 없는데요? -그렇다고 내 자신을 죽일 순 없잖아요..?)

수고했다 나 자신