트리를 알게되면서 새로운 자료구조가 많이 드러났다. 15장에서는 특히 이진 탐색 트리에 중점을 뒀으나 다른 트리의 종류도 많다. 모든 자료 구조가 그렇듯 각 트리 종류마다 장단점이 존재하고 특정 상황에서 어떻게 활용해야 할지 아는 것이 중요하다.

16장에서는 특정 시나리오에 유리하게 활용할 수 있는 트리 자료 구조 중 하나인 힙을 알아볼 예정이다. 힙은 데이터 세트에서 가장 큰, 또는 가장 작은 데이터 원소를 계속 알아내야 할 때 유용하다.

힙을 제대로 알아보기 전에 먼저 우선순위 큐부터 살펴보자.

16.1 우선순위 큐

우선순위 큐(Priority Queue)란?
우선순위 큐(Priority queue)는 일반 큐나 스택과 비슷한 축약 자료형이다. 그러나 각 원소들은 우선순위를 갖고 있다. 우선순위 큐에서, 높은 우선순위를 가진 원소는 낮은 우선순위를 가진 원소보다 먼저 처리되고, 만약 두 원소가 같은 우선순위를 가진다면 그들은 큐에서 그들의 순서에 의해 처리된다.

9장에서 배웠던 큐는 FIFO(First-In-First-Out) 구조로 항목을 처리하는 리스트(list)였다. 큐는 큐의 끝에서만 데이터를 삽입하고, 큐의 앞에서만 데이터에 대한 접근과 삭제를 수행한다. 큐의 데이터에 접근하기 위해서는 데이터가 삽입됐던 순서에 우선권이 있다.

우선순위 큐(priority queue)는 삭제와 접근에 있어 전형적인 큐와 흡사하나, 삽입에서는 정렬된 배열과 비슷한 리스트다. 즉, 우선순위 큐 앞에서만 데이터에 접근하고 삭제하되 데이터를 삽입할 때에는 늘 특정 순서대로 정렬시킨다.

우선순위 큐가 유용하게 쓰이는 대표적인 예는 병원 응급실의 중증도 분류체계 관리 애플리케이션이다. 응급실에서는 도착한 순서를 엄격히 따져 환자를 치료하지 않는다. 대신 중증도에 따라 치료한다. 치명상을 입은 환자가 갑자기 도착하면 감기게 걸린 환자가 먼저 도착했더라도 치명상 환자를 우선순위 큐의 맨 앞에 놓는다.

중증도 분류체계에서 환자의 중증도를 1부터 10까지 등급으로 분류한다고 했을 때, 10이 가장 위험한 상태이다.

중증도 분류	위치
환자 C - 중증도 10	👈 우선순위 큐의 앞
환자 A - 중증도 6
환자 B - 중증도 4
환자 D - 중증도 2

여기에서 치료할 환자를 정할 때, 항상 우선순위 큐의 앞에 있는 환자(가장 급하게 치료해야 할 환자)를 고른다. 위 예제에서는 환자 C 라고 할 수 있다. 만약 이 상태에서 중증도가 3인 환자가 도착했다면, 해당 환자를 우선순위 큐 내 적절한 위치에 넣는다. (환자 E)

중증도 분류	위치
환자 C - 중증도 10	우선순위 큐의 앞
환자 A - 중증도 6
환자 B - 중증도 4
환자 E - 중증도 3
환자 D - 중증도 2

우선순위 큐는 추상 데이터 타입의 하나의 예이다. 다시 말하면 보다 기초적인 다른 자료 구조로 구현할 수 있다. 우선순위 큐를 간단하게 구현하려면 정렬된 배열을 이용할 수 있다. 배열을 사용하되 아래와 같은 제약이 필요하다.

• 데이터를 삽입할 때 항상 적절한 순서를 유지한다.
• 데이터는 배열의 끝에서만 삭제한다. (배열의 끝 = 우선순위 큐의 앞)

효율성을 분석해보면, 우선순위 큐의 주요 연산은 삭제와 삽입이다.

1장-자료구조가 중요한 까닭에서 살펴보았듯 배열의 앞에서 이뤄지는 삭제는 인덱스 0의 자리에 생긴 빈 자리를 메우기 위해 모든 데이터를 한 자리씩 시프트해야 하므로 $O(N)$이다. 하지만 영리하게 구현을 바꿔 배열의 끝을 우선순위 큐의 앞으로 삼으면, 항상 배열의 끝에서 삭제하니 $O(1)$이다.

🙄 아직은 우선순위 큐에 문제가 없다. 하지만 삽입은 어떨까?

정렬된 배열에 삽입은 새 데이터를 넣을 자리를 알아내기 위해 배열의 원소 $N$개를 모두 확인해야 하므로 $O(N)$이다. 따라서 배열 기반의 우선순위 큐는 삭제가 $O(1)$, 삽입이 $O(N)$이다.

우선순위 큐에 항목이 많아지면 $O(N)$ 삽입으로 인해 애플리케이션에 지연이 발생할 수 있다.
그래서 컴퓨터 과학자는 우선순위 큐에서 보다 효율적인 기반으로 쓰일 또 다른 자료구조를 찾아냈다.
그것이 바로 힙이다.

16.2 힙

힙(Heap)이란?
최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전 이진 트리를 기본으로 한 자료구조

이진 힙(Binary Heap)이란?
이진 트리 형태를 취하는 힙 자료 구조로, 우선순위 큐를 구현하는 일반적인 방법이다.

힙에는 몇 가지 종류가 있으나 이진 힙을 주로 다루겠다.
이진 힙에도 최대 힙(max-heap)과 최소 힙(min-heap) 두 종류가 있다.

(최대 힙을 우선으로 다룰 것이나 최소 힙와 최대 힙은 큰 차이가 없다.)

힙은 다음의 조건을 따르는 이진 트리이다.

• 각 노드의 값은 그 노드의 모든 자손 노드의 값보다 커야 한다. (= 힙 조건 heap condition)
• 트리는 완전(complete)해야 한다.

힙 조건

힙 조건(Heap Condition)이란?
각 노드의 값이 그 노드의 모든 자손 노드보다 커야한다는 힙의 속성

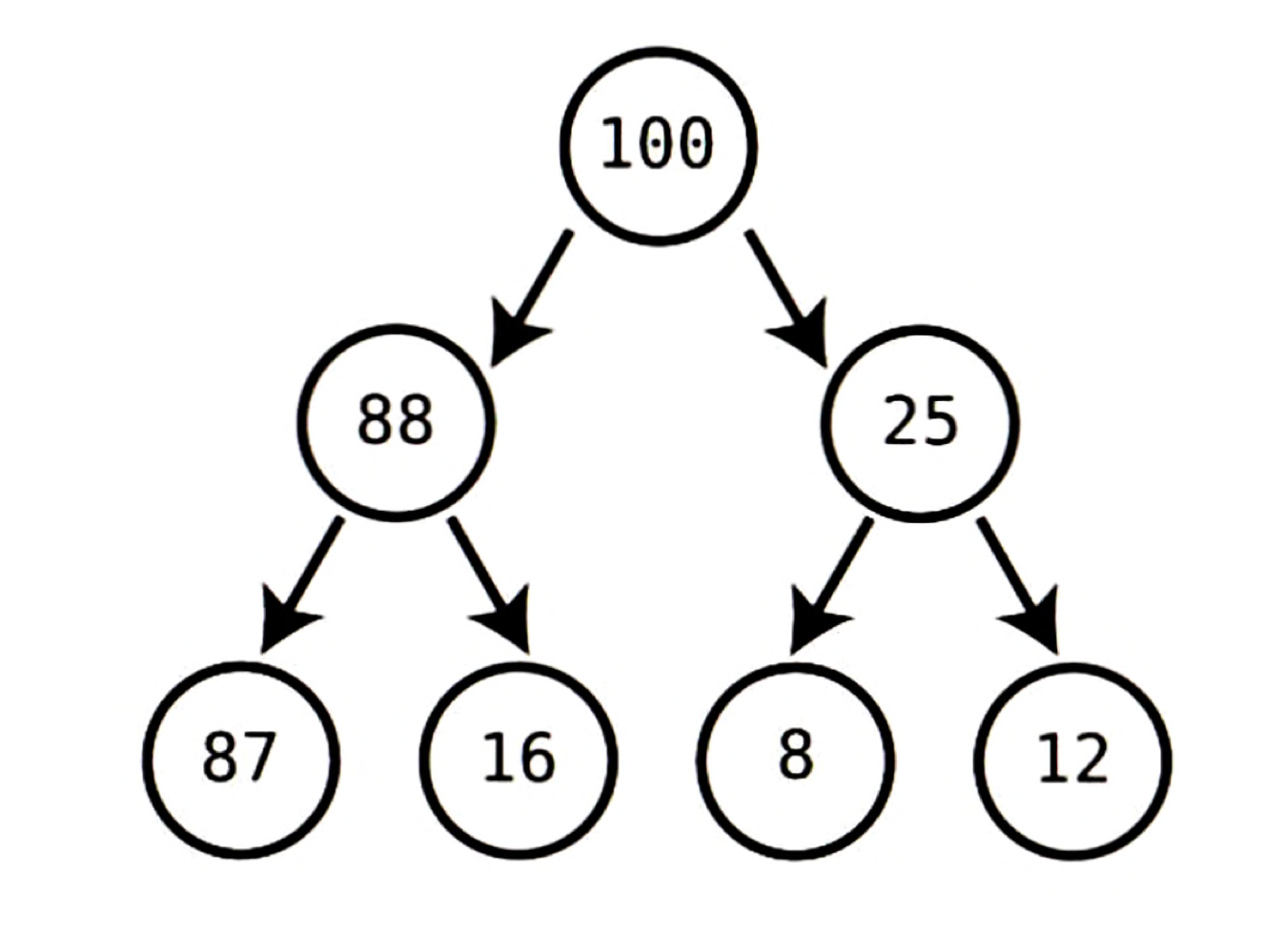
예를 들어 위 트리에서 각 노드는 그 자손보다 크므로 힙 조건을 만족한다.

루트 노드인 100에 100보다 큰 자손은 없다.
마찬가지로 88은 두 자식보다 크고, 25도 자신의 자식보다 크다.

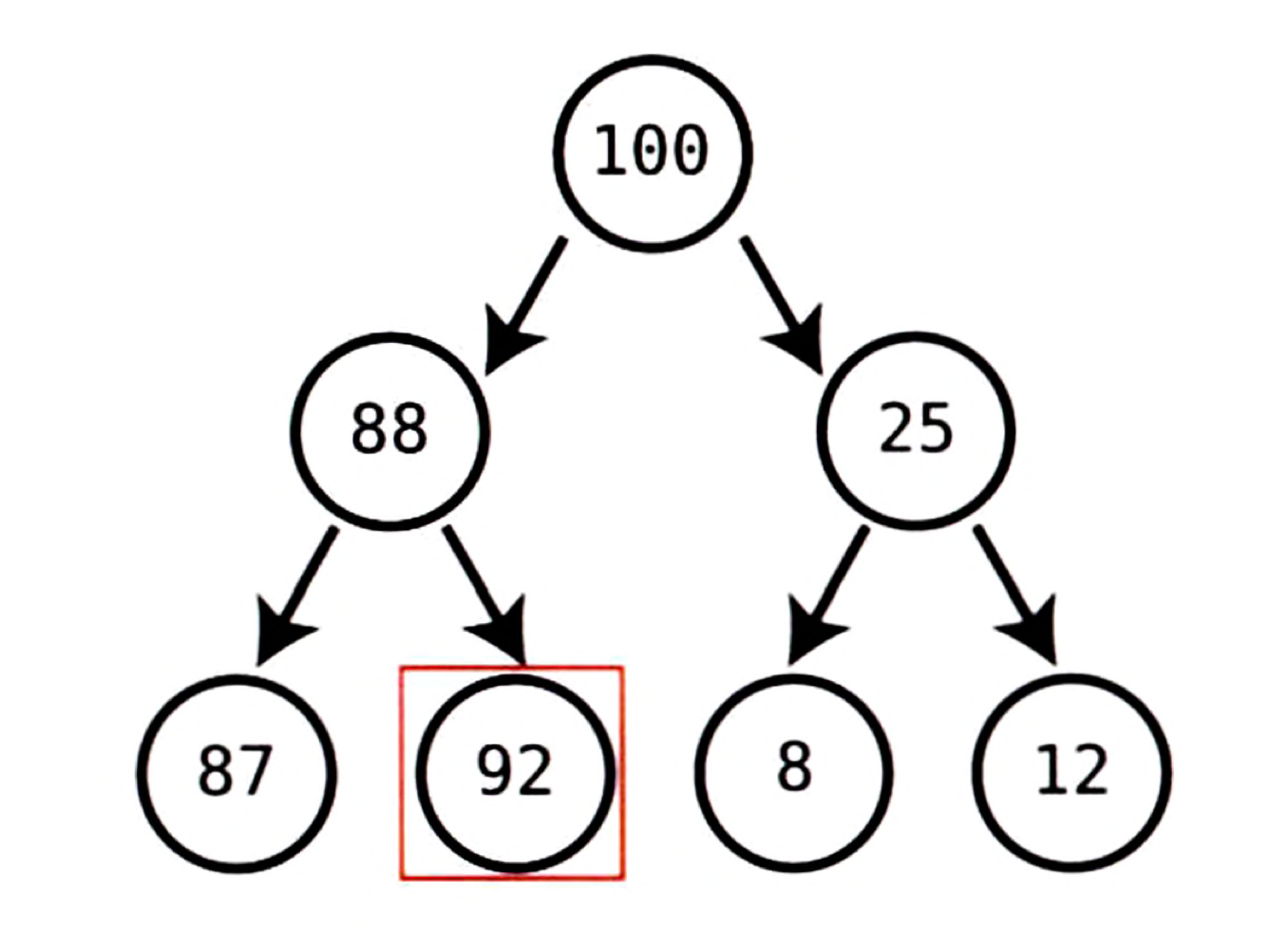
위 트리는 마지막 레벨의 노드인 92가 부모인 88보다 크기 때문에 힙 조건을 만족하지 않아 유효한 힙이 아니다.

힙은 이진 탐색 트리와 매우 다르게 조직된다. 이진 탐색 트리에서 각 노드의 오른쪽 자식은 해당 노드보다 크지만, 힙에서는 각 노드는 해당 노드의 모든 자손보다 크다.

정반대의 힙 조건으로도 힙을 구성할 수 있다. 즉, 각 노드가 자손보다 작은 값을 갖도록 할 수 있다.
이러한 힙을 최소 힙(min-heap)이라고 부른다.

최대 힙과 최소 힙의 근본적인 개념은 같으며, 힙 조건만 반대일 뿐이다.
최대 힙과 최소 힙 중 어떤 것을 사용하던 차이는 미미하다. (이 책에서는 최대 힙에 초점을 맞춰 진행)

완전 트리

트리가 완전해야 한다는 두 번째 힙의 규칙을 살펴보면, 완전 트리(complete tree)는 빠진 노드가 없이 노드가 완전히 채워진 트리다. 따라서 트리의 각 레벨을 왼쪽부터 오른쪽으로 읽었을 때, 모든 자리마다 노드가 존재한다. 하지만 바닥 줄에는 빈 자리가 있을 수 있다. 다만 빈 자리의 오른쪽으로 어떤 노드도 없어야 한다.

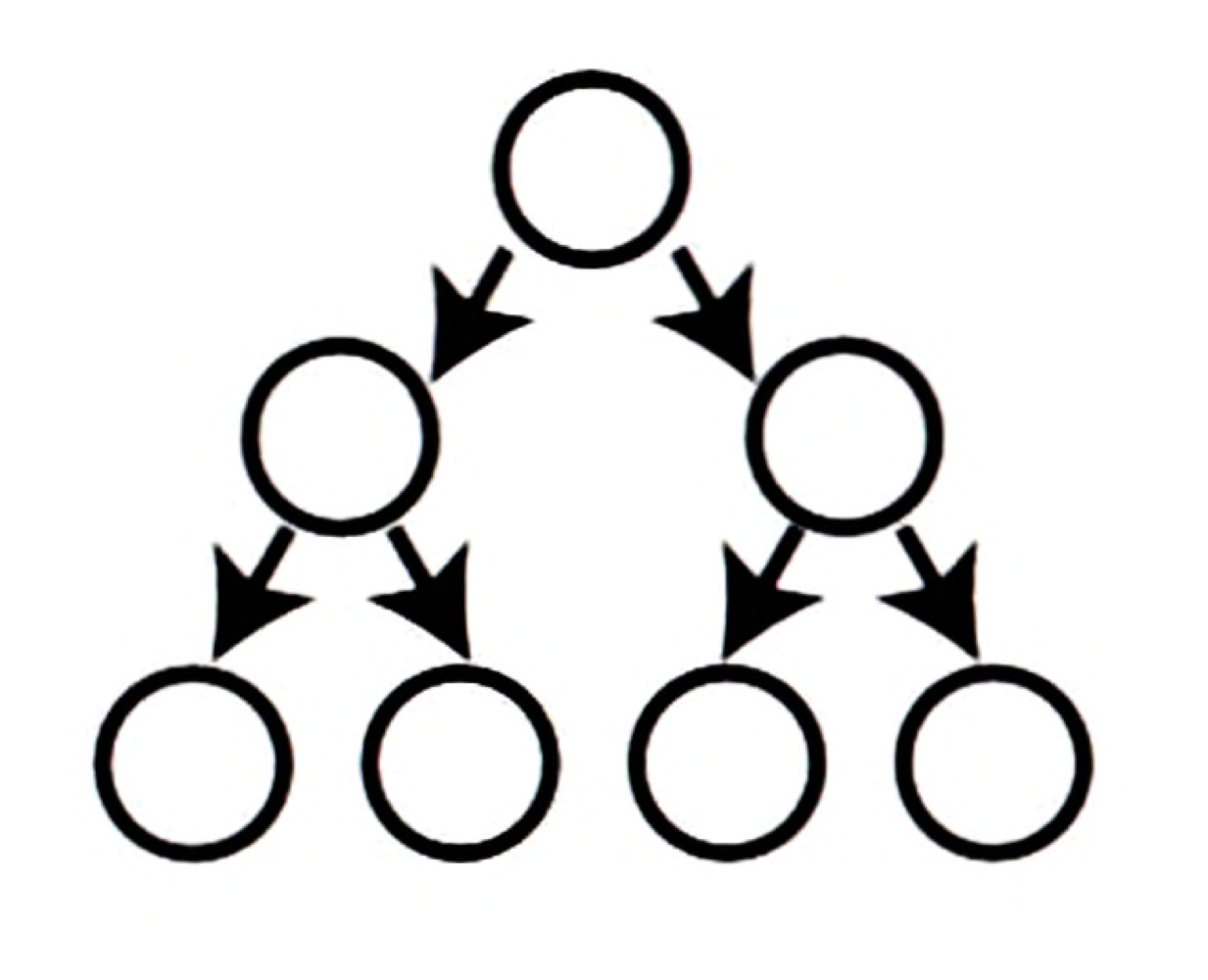
위 트리는 트리의 각 레벨이 노드로 완전히 채워져 있으므로 완전 트리다.

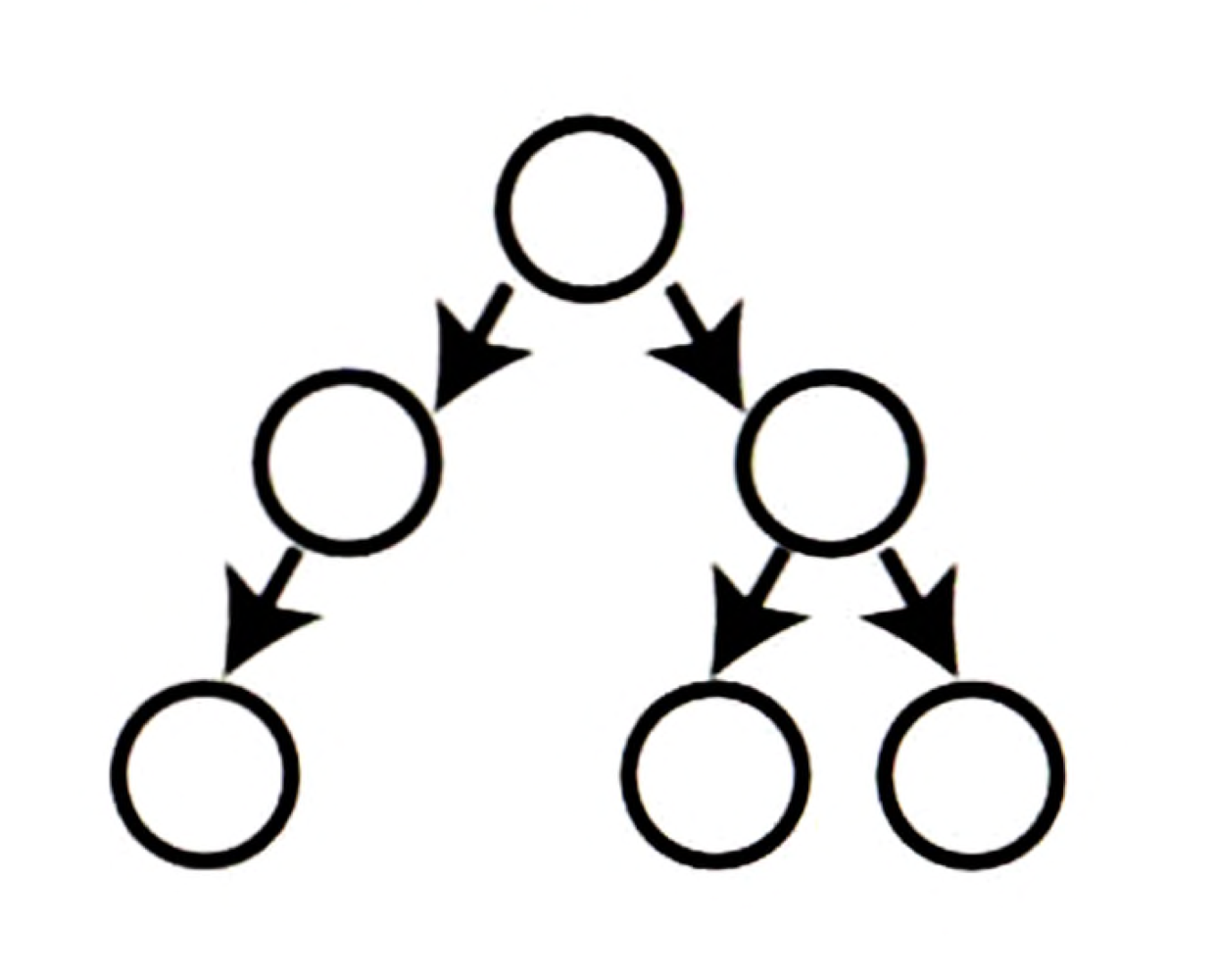
위 트리는 세 번째 레벨 중 하나의 노드가 빠져있으므로 완전 트리가 아니다.

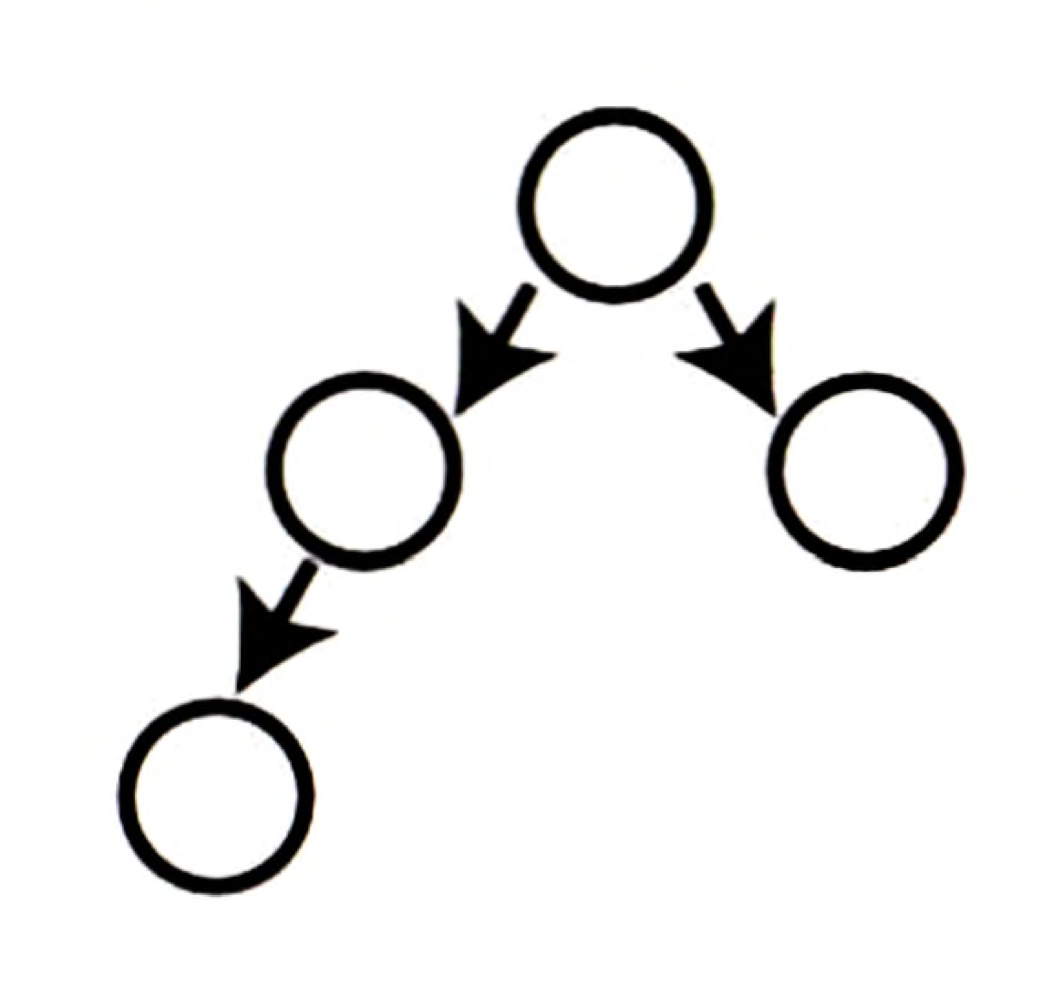
위 트리는 마지막 레벨에 빈 자리가 있으나, 빈 자리의 오른쪽으로 어떤 노드도 없으므로 완전 트리다.

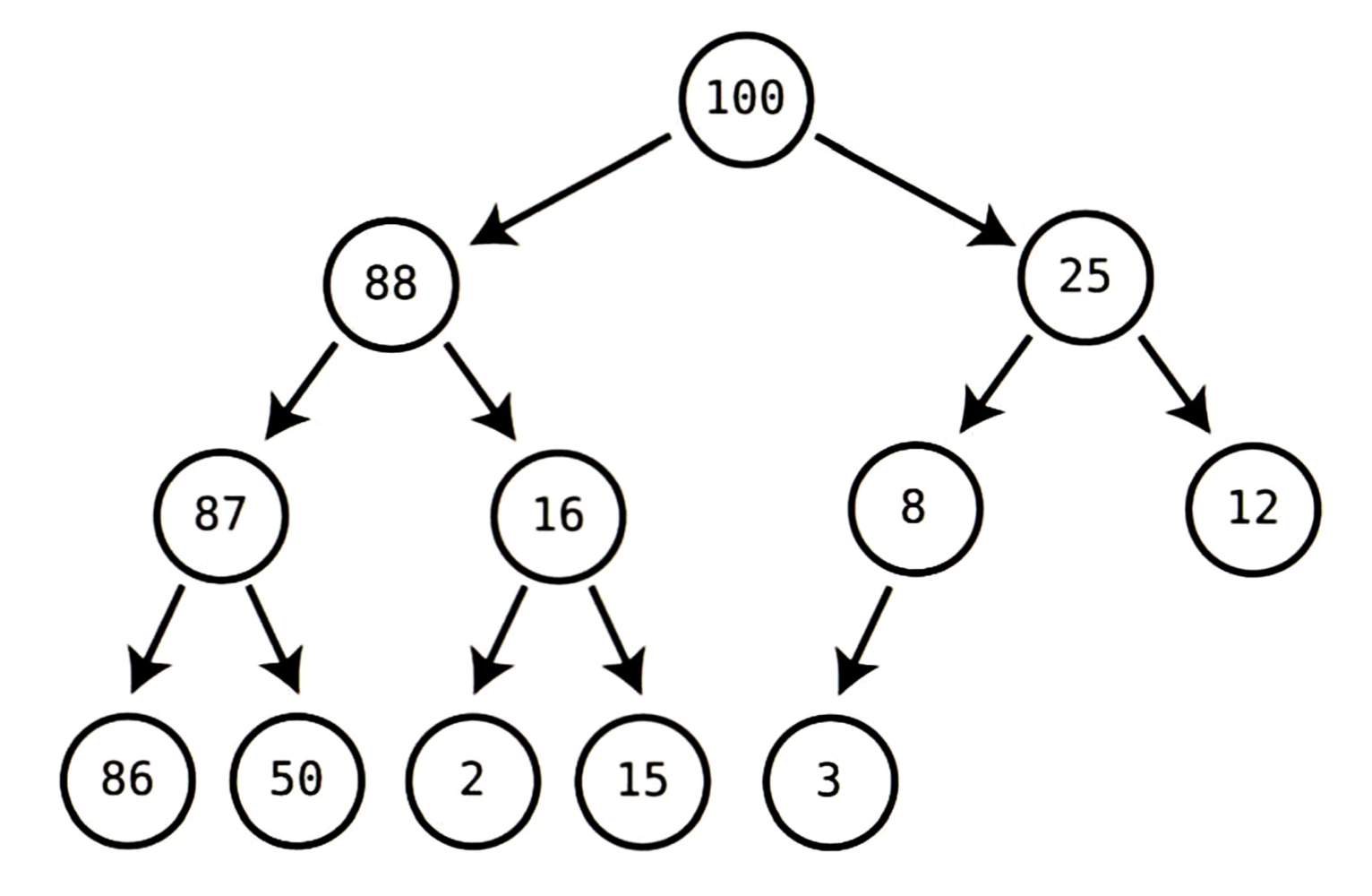
위 트리는 각 노드가 자손보다 크고, 트리가 완전하므로 유효한 힙이다.

결국 힙(heap)은 힙 조건을 만족하는 완전 트리라고 할 수 있다.

16.3 힙 속성

힙 조건에 따라 힙은 특정 방식으로 정렬되지만, 이러한 정렬은 힙에서 값을 검색하는데 전혀 도움되지 않는다.

예를 들어 위 트리에서 3을 검색한다고 한다면,
루트 노드인 100에서 시작했을 때 왼쪽 자손과 오른쪽 자손 중 어느 쪽을 검색해야 할까?

이진 탐색 트리의 경우 당연히 3이 100의 왼쪽 자손일 것이다. 3이 100보다 작기 때문이다.
하지만 힙에서는 3이 100의 조상이 아니라 자손이라는 것만 알 수 있고, 어느 자식을 검색해야 할지는 알 수 없다.
실제로 3은 100의 오른쪽 자손이지만, 왼쪽 자손일 수도 있다.

따라서 힙은 이진 탐색 트리에 비해 약한 정렬(weakly ordered)이라고 말한다.
힙에는 자손이 조상보다 클 수 없다는 분명한 순서가 존재하지만, 어떤 값을 검색하기에는 부족하다.

또 하나의 힙 속성은 힙에서 루트 노드가 항상 최댓값이는 점이다. (최소 힙에서는 루트 노드가 항상 최솟값이다.)
이 대목이 바로 힙이 우선순위 큐를 구현하는 훌륭한 도구라는 것을 말해주는 대목이다.

우선순위 큐에서는 항상 큰 우선순위를 가지는 값에 접근하려 한다. 힙에서는 항상 루트 노드가 된다.
다시 말해, 루트 노드가 가장 높은 우선순위를 갖는 항목에 해당한다.

힙의 주요 연산은 삽입과 삭제로, 힙에서 검색을 하기 위해서는 각 노드를 검사해야 하므로 대게 검색 연산을 구현하지 않는다.

힙의 주요 연산이 어떻게 동작하는지 알아보기에 앞서 앞으로 나올 알고리즘에 많이 쓰일 용어를 정의해보면,
힙에는 마지막 노드(last node)가 존재한다. 힙의 마지막 노드는 바닥 레벨에서 가장 오른쪽에 위치한 노드이다.

위 그림 예제에서 마지막 노드는 3이다.

16.4 힙 삽입

힙에 새로운 값을 삽입하기 위해서는 다음 알고리즘을 수행한다.

1. 새로운 값을 포함하는 노드를 생성하고, 바닥 레벨의 가장 오른쪽 노드 옆에 삽입한다.
   즉, 이 값이 힙의 마지막 노드가 된다.
2. 이어서 새로 삽입한 노드와 그 부모 노드를 비교한다.
3. 새로운 노드가 부모 노드보다 크면, 새 노드를 부모 노드와 스왑한다.
4. 새로운 노드보다 큰 부모 노드를 만날 때까지 3번째 단계를 반복하며 새 노드를 힙의 위로 올린다.

앞서 보았던 예제에 새로운 노드 40를 삽입하는 과정을 살펴보자.

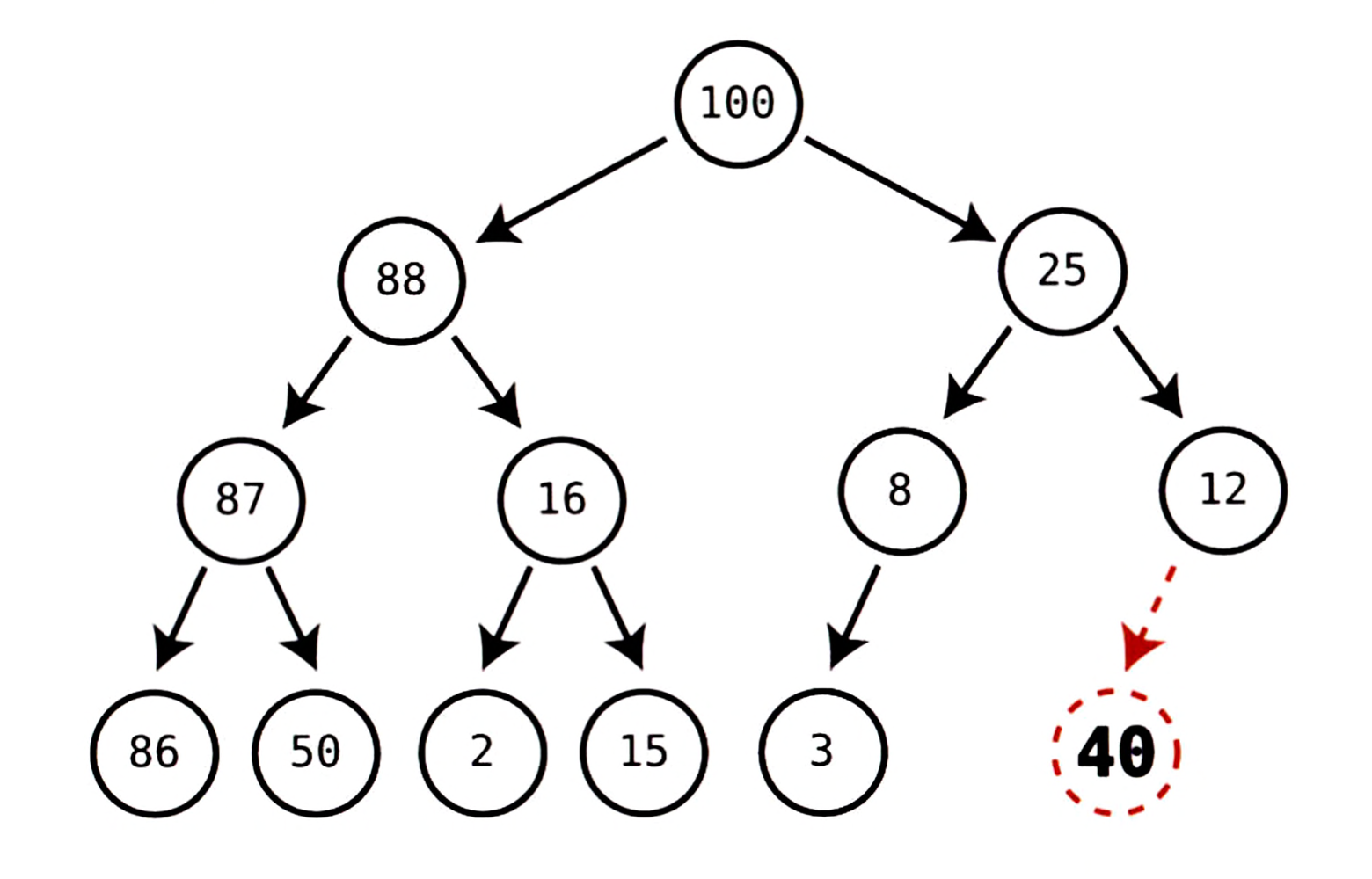
1단계: 힙의 마지막 노드로 40을 추가한다.
(노드 8의 자손으로 넣지 않도록 주의하자.)

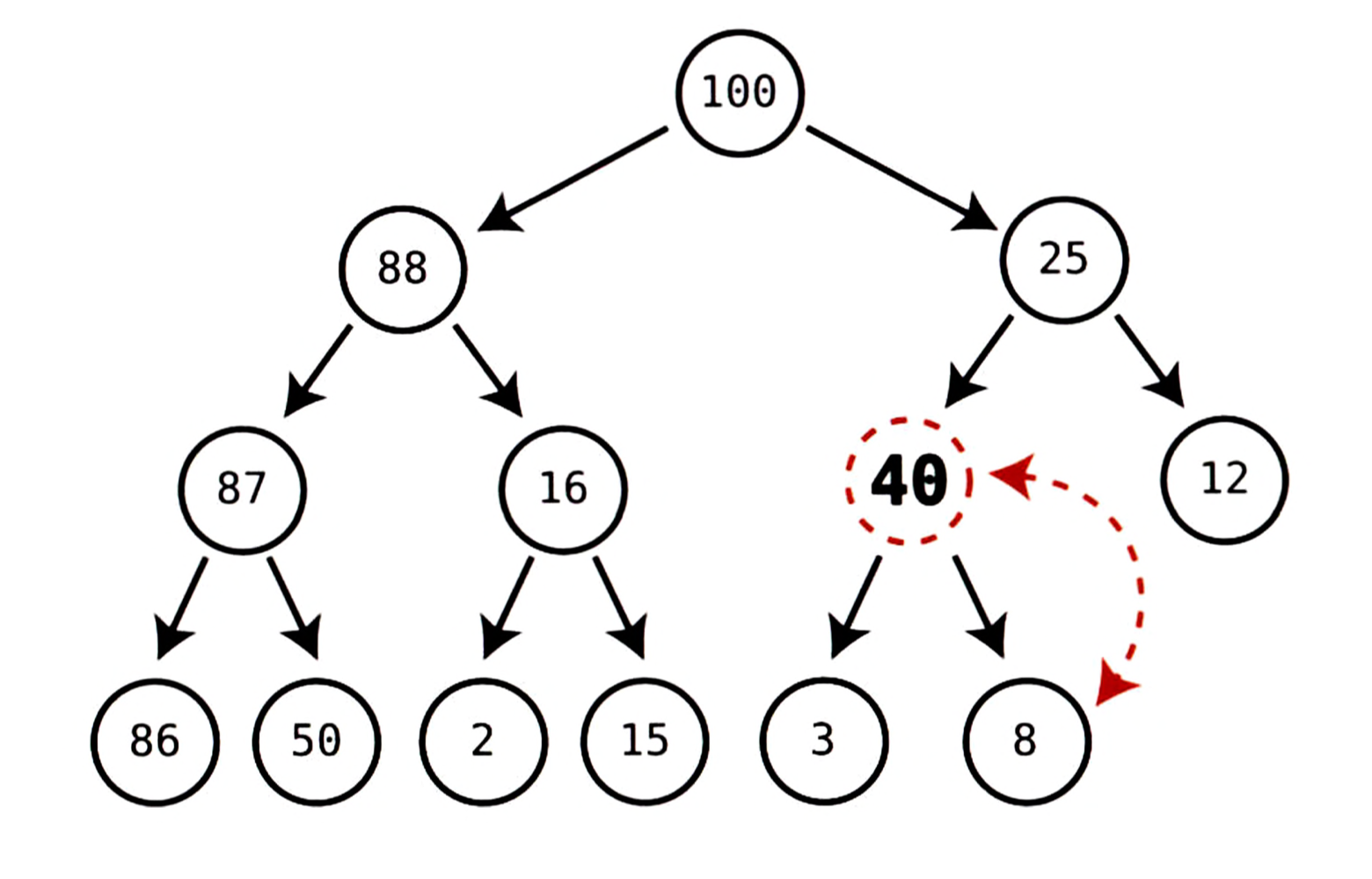
2단계: 40을 그 부모 노드인 8과 비교한다. 40이 8보다 크므로 두 노드를 스왑한다.

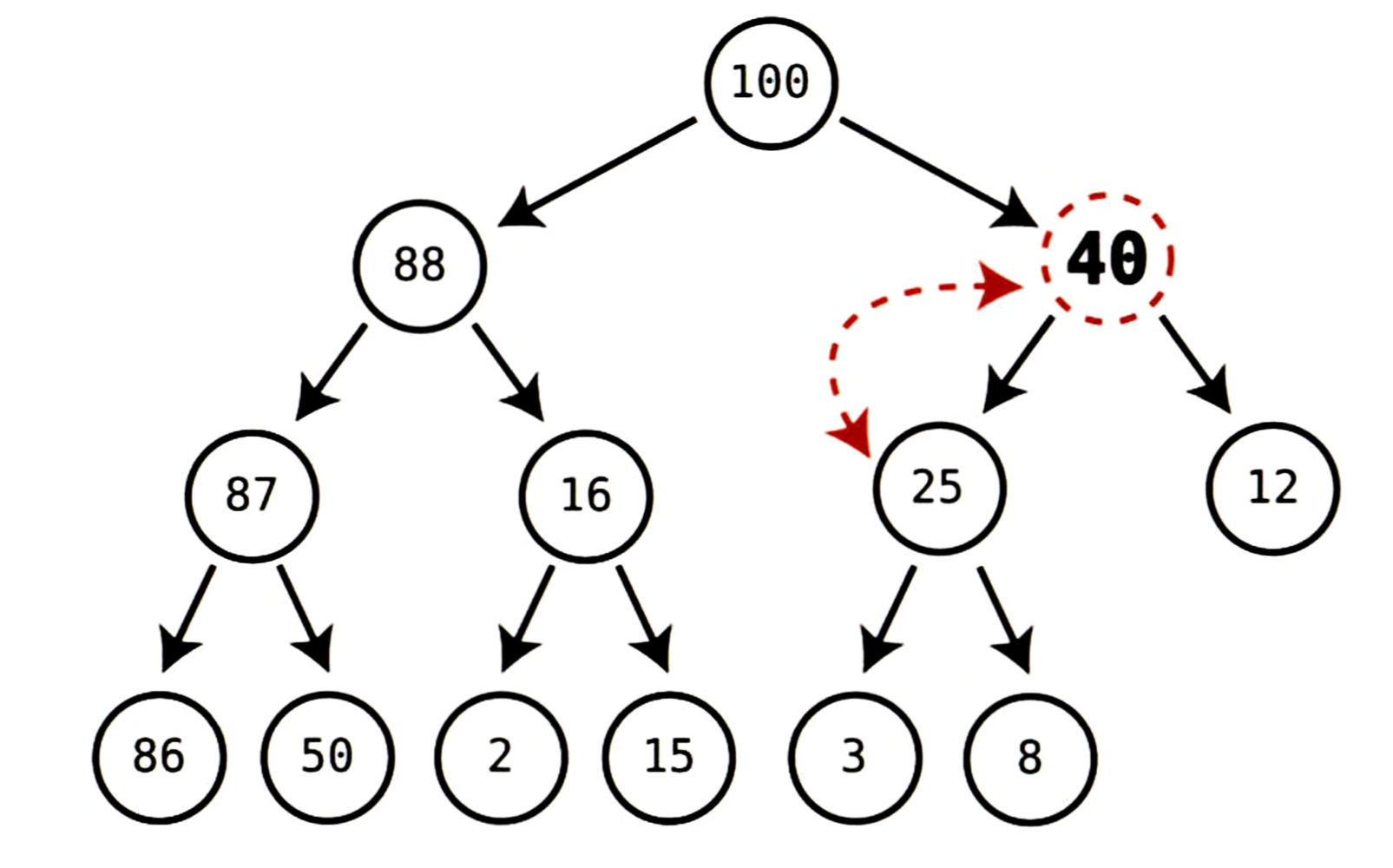
3단계: 40을 새 부모 노드인 25와 비교한다. 40이 25보다 크므로 두 노드를 스왑한다.

4단계: 40을 그 부모 노드인 100과 비교한다. 40은 100보다 작으므로 여기에서 끝난다.

새 노드를 힙의 위로 올리는 과정을 노드를 위로 트리클링(trickling)한다고 표현한다.
때로는 오른쪽으로, 때로는 왼쪽으로 올라가지만 올바른 위치에 안착할 때까지 항상 위로 올라간다.

힙에서 삽입의 효율성은 $O(logN)$이다. 노드가 $N$개인 이진 트리는 약 $log(N)$개의 줄을 갖는다.
최악의 경우 새 값을 꼭대기 줄까지 트리클링 해야하므로 최대 $log(N)$단계가 소요된다.

16.5 마지막 노드 탐색

삽입 알고리즘은 간단해 보이지만 작은 문제를 가지고 있다.
가장 첫 단계에서 새로운 값을 힙의 마지막 노드로 넣는데, 과연 마지막 노드의 자리를 어떻게 찾을까?

40이 마지막 노드가 되기 위해서는 바닥 줄에서 다음으로 노드를 넣을 수 있는 자리인 8의 오른쪽 자식으로 넣어야 한다. 하지만 컴퓨터는 눈이 없기 때문에 힙을 위 그림 예제처럼 보지 못한다. 루트만 보이고 링크를 따라 자식 노드에 갈 수 있다.

🤔 컴퓨터가 새로운 값을 넣을 자리를 찾는 알고리즘을 어떻게 만들까?

근본적으로 힙에서 검색하기가 불가능하듯이 힙의 마지막 노드(혹은 새로운 노드가 들어갈 다음 자리)도 모든 노드를 검사하지 않고는 효율적으로 찾을 수 없다. 이 이슈를 마지막 노드 문제(Problem of the Last Node)라고 부르기로 하고. 잠시 후 자세히 살펴보겠다.

16.6 힙 삭제

힙에서 값을 삭제하려면 루트 노드만 삭제할 수 있다.
이유는 가장 높은 우선순위를 갖는 항목에만 접근과 삭제가 가능하다는 우선순위 큐의 동작 방식 때문이다.

1. 마지막 노드를 루트 노드 자리로 옮긴다. (결과적으로 루트 노드는 삭제된다.)
2. 루트 노드를 적절한 자리까지 아래로 트리클링 한다.

위 트리에서 루트 노드인 100을 삭제 하기 위해서는 마지막 노드를 루트에 덮어쓴다.
마지막 노드는 3이므로, 100이 있던 자리에 3을 집어넣는다.

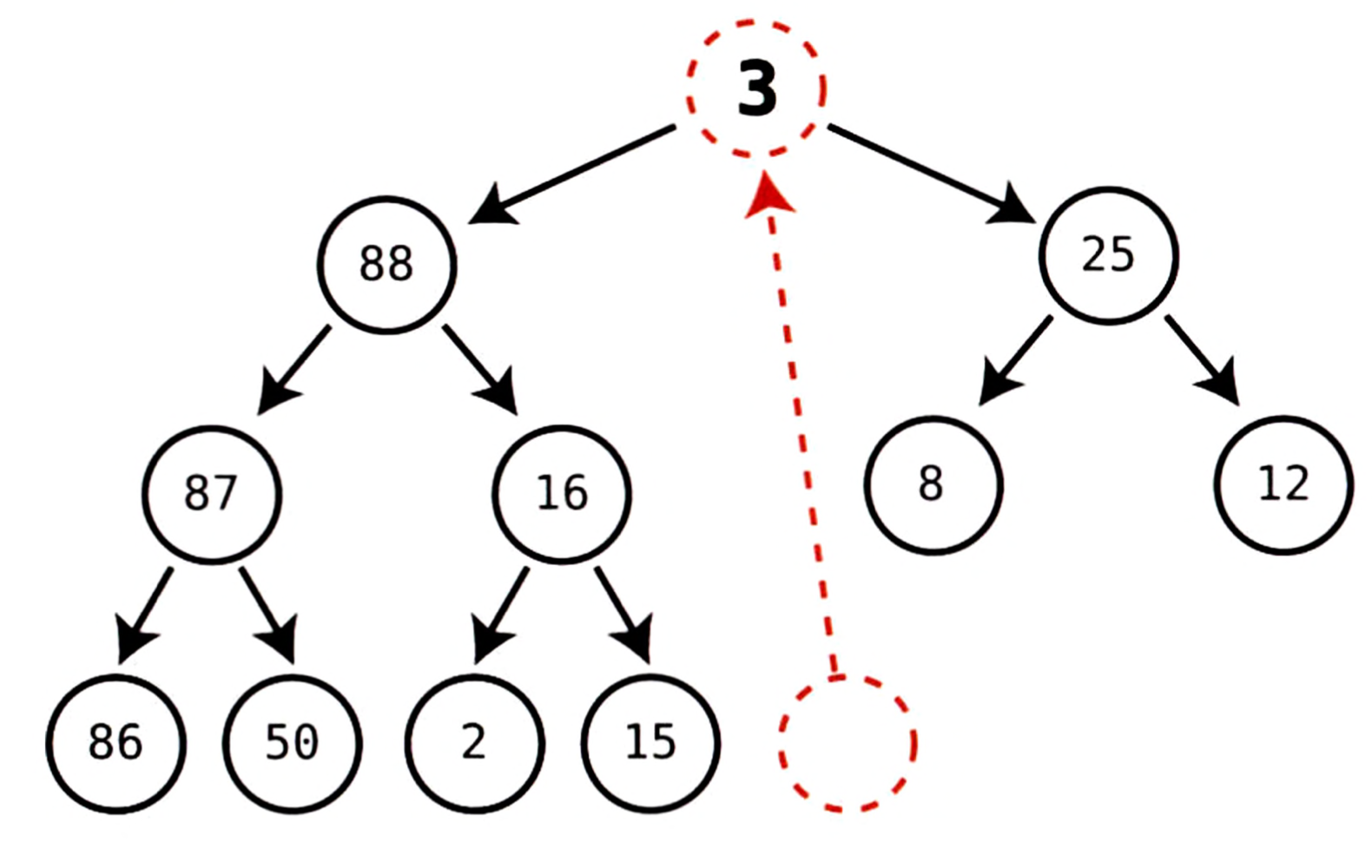
하지만 이 상태에서는 힙 조건이 깨졌기 때문에 이대로 힙을 유지하면 안 된다.
현재 루트 노드인 3은 대부분의 자손보다 작으므로, 이를 바로잡기 위해 3을 아래로 트리클링해야 한다.

노드를 아래로 트리클링할 때 내려갈 수 있는 방향이 두 개이기 때문에, 아래로 트리클링 하는 방법은 위로 트리클링 하는 방법보다 조금 더 복잡하다. 즉 왼쪽 자식과 스왑할 수도 있고, 오른쪽 자식과 스왑할 수도 있다.

1. 트리클링하는 노드의 두 자식을 확인해 어느 쪽이 더 큰지 본다.
2. 트리클링하는 노드가 두 자식 노드 중 큰 노드보다 비교하여 큰 노드보다 작으면 스왑한다.
3. 트리클링하는 노드의 자식 노드 중, 트리클링 노드보다 큰 자식이 없을 때까지 1~2단계를 반복한다.

1. 현재 트리클 노드인 3은 88과 25를 자식으로 두고 있다.
   둘 중 88이 더 크고, 3이 88보다 작으므로 3과 88을 스왑한다.

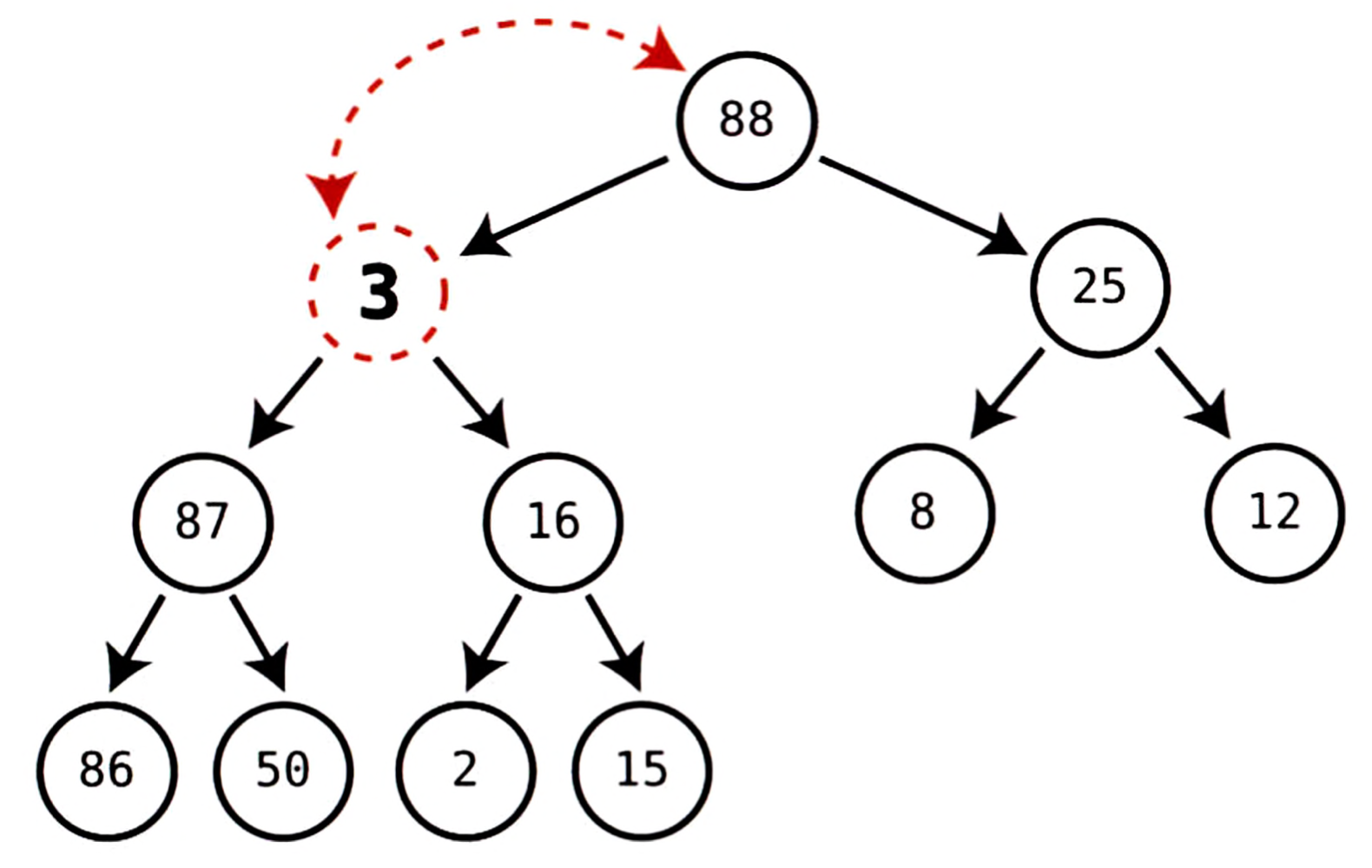
2. 이제 트리클 노드에 87과 16 두 자식이 있다.
   둘 중 87이 더 크고, 3이 87보다 작으므로 3과 87을 스왑한다.

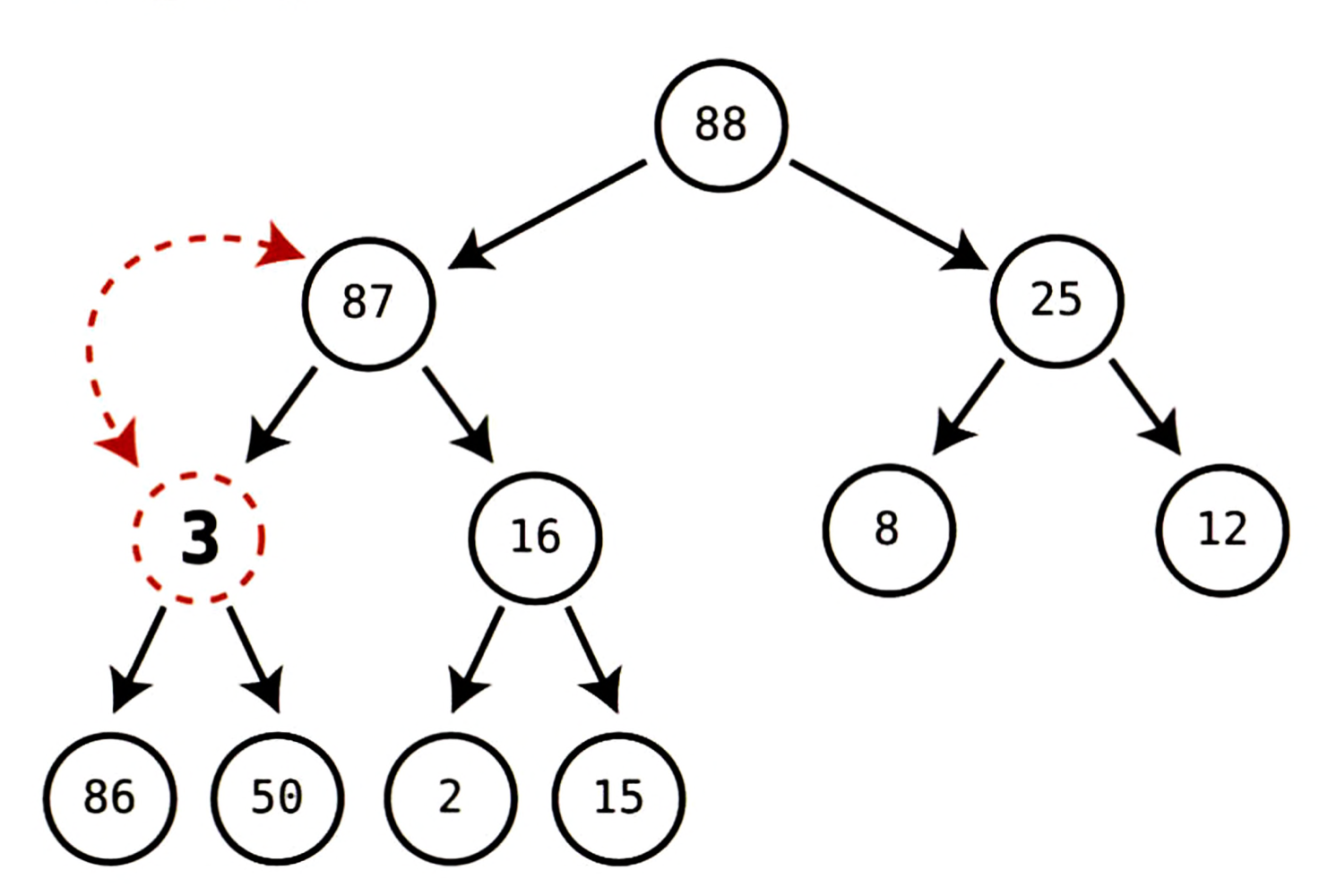
3. 다시 현재 트리클 노드는 86과 50 두 자식을 가지고 있다.
   둘 중 86이 크고, 3은 86보다 작으므로 3과 86을 스왑한다.

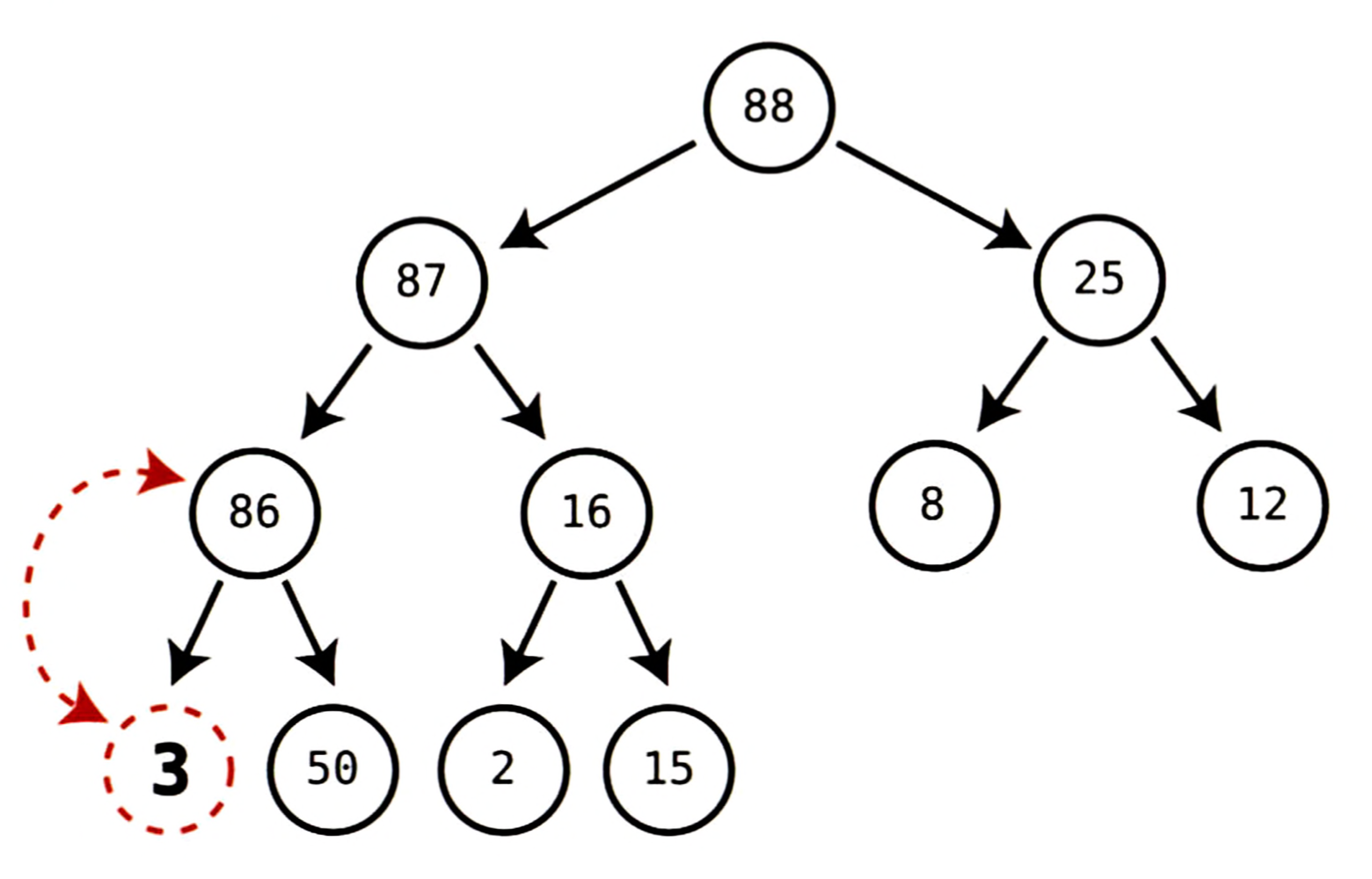
이제 트리클 노드에 자기보다 큰 자식이 없다. 힙 조건을 만족하므로 여기에서 끝난다.

트리클 노드와 두 자식 중 더 큰 노드를 비교하여 스왑하는 이유는 작은 노드와 스왑하면 힙 조건이 바로 깨지기 때문이다. 만약 루트 노드에 있던 3을 자식 중 작은 값이었던 25와 스왑한다면 25가 88의 부모가 되므로 힙 조건이 깨지게 된다.

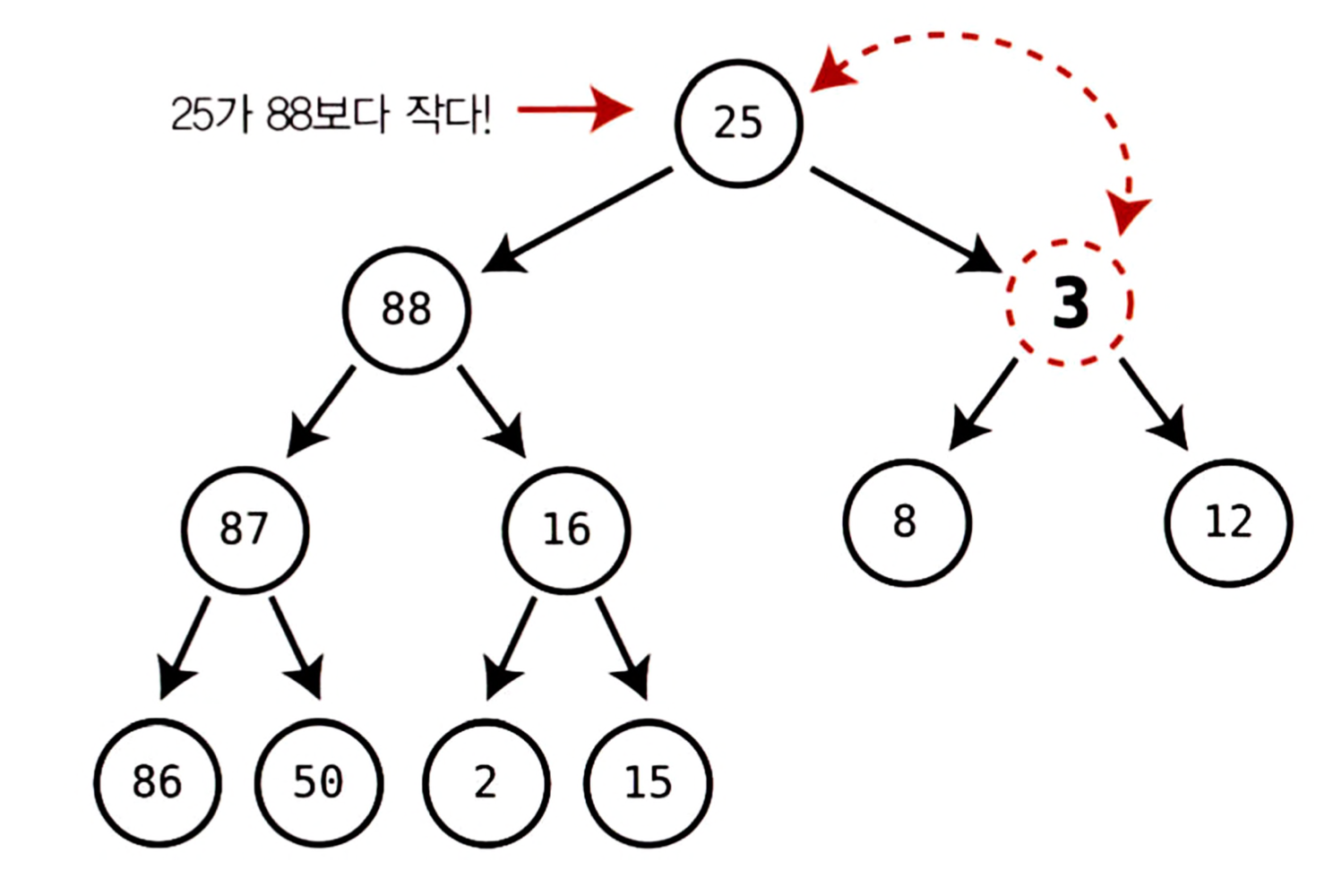
힙에서 삭제하려면 루트부터 시작해 $log(N)$개 레벨을 거쳐 노드를 트리클링해야 하므로 삽입과 마찬가지로 $O(logN)$의 시간복잡도를 가진다.

16.7 힙 대 정렬된 배열

이제 힙이 왜 우선순위 큐를 구현하는 훌륭한 방식인지 알아보자.

	정렬된 배열	힙
삽입	$O(N)$	$O(logN)$
삭제	$O(1)$	$O(logN)$

정렬된 배열에서 삽입은 힙보다 느리지만, 삭제는 힙보다 빠르다. 하지만 그럼에도 불구하고 힙을 선택하는 것이 더 낫다. 왜냐하면 $O(1)$이 엄청 빠르긴 하지만 $O(logN)$도 매우 빠르기 때문이다. 반면에 $O(N)$은 느리다.

	정렬된 배열	힙
삽입	느림	매우 빠름
삭제	엄청나게 빠름	매우 빠름

때로는 엄청 빠르고 때로는 엄청 느린 자료구조보다는 일관되게 매우 빠른 자료구조를 사용하는 편이 낫다.

우선순위 큐가 삽입과 삭제를 비슷한 비율로 수행한다는 것에 주목해보면, 응급실 중증도 분류와 같은 예제에서 삽입과 삭제 두 연산 모두 빨라야 한다. 어느 하나라도 느리다면 우선순위 큐의 효율성이 떨어지게 된다. 따라서 우선순위 큐의 주요 연산인 삽입과 삭제를 빠른 속도로 수행하기 위해서는 힙을 사용해야 한다.

16.8 다시 살펴보는 마지막 노드 문제

힙에서 삭제 알고리즘이 간단해 보여도 '마지막 노드 문제(Problem of the Last Node)'가 존재한다.
힙에서 삭제의 첫 번째 단계는 마지막 노드를 루트 자리로 옮기는 것이었다.

하지만 마지막 노드를 어떻게 찾을까?

마지막 노드 문제를 풀기 전에 삽입과 삭제에 왜 마지막 노드가 필요한지 알아야 한다.

• 새로운 값을 힙의 다른 위치에 삽입하면 안 되는 이유는, 이 경우 힙이 불완전해지기 때문이다.
• 힙에서 완전성(completeness)이 중요한 이유는 균형 잡힌 힙을 유지하기 위함이다.

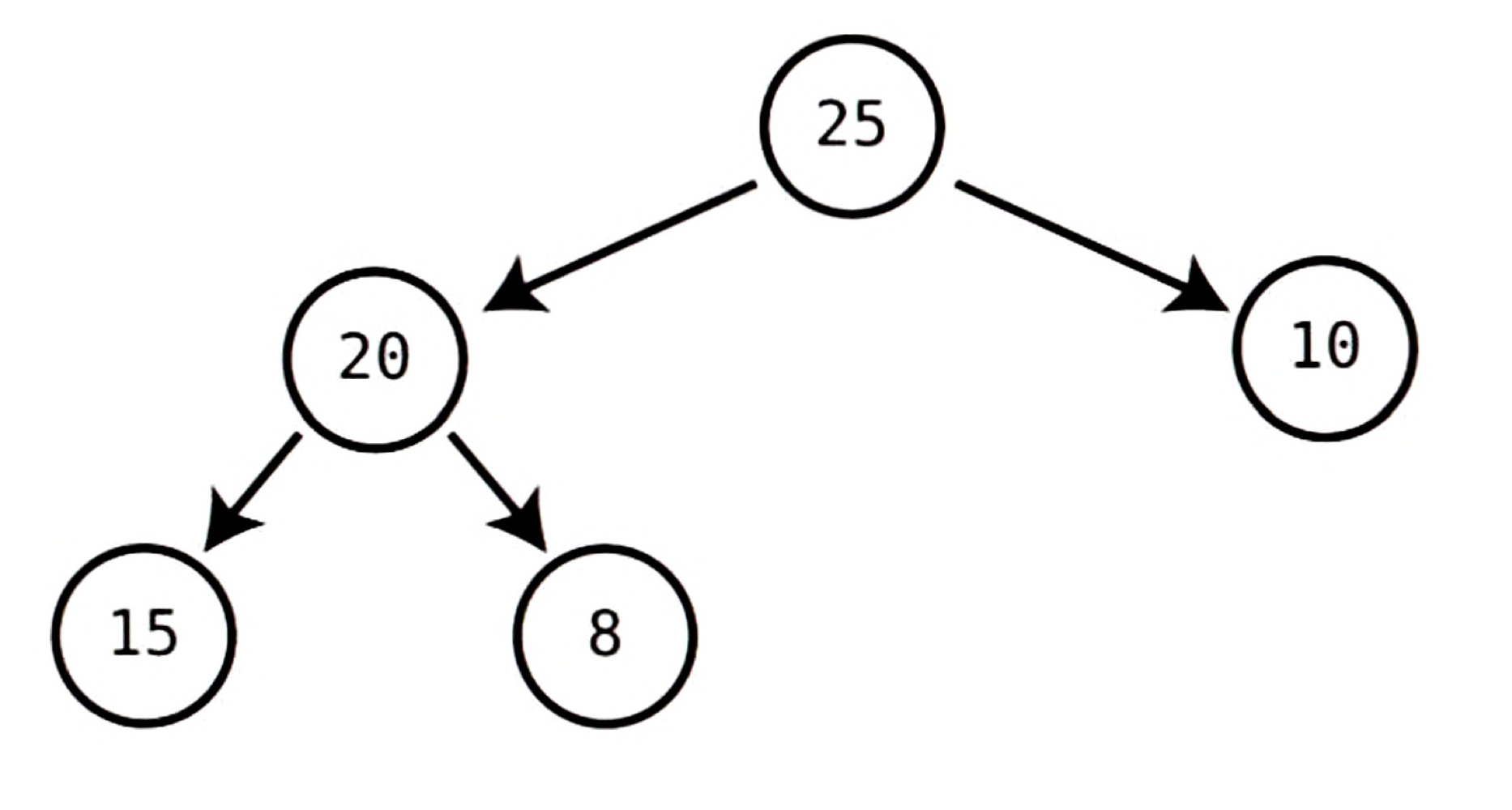
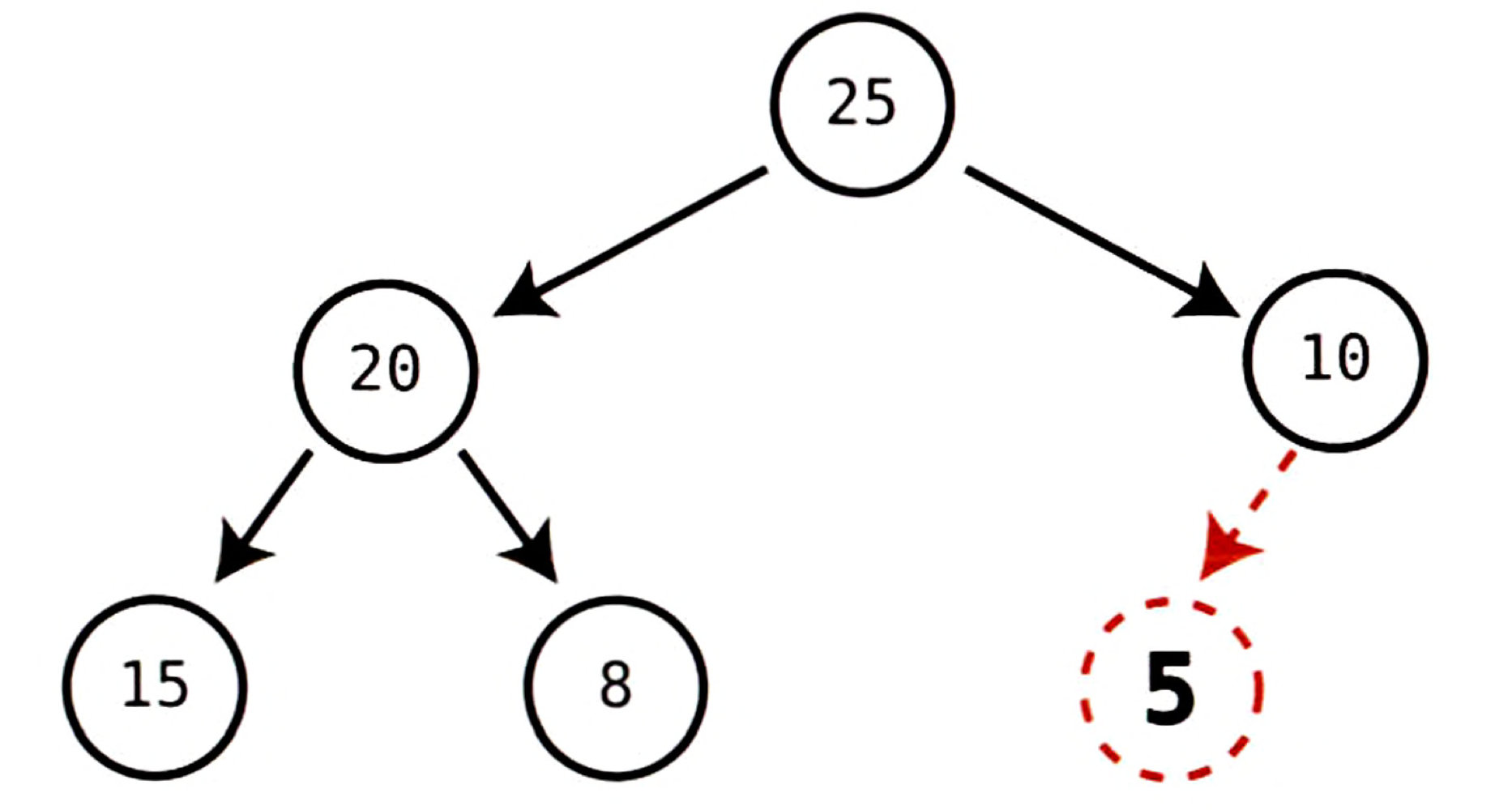
위 힙에서 새로운 노드로 5를 삽입할 때 균형 잡힌 힙을 유지할 방법은 5를 10의 자식인 마지막 노드로 만드는 방법 뿐이다. 이 알고리즘을 외 다른 방법은 트리의 불균형을 초래한다.

만약 어떤 알고리즘이 왼쪽 자식만 따라가면 쉽게 찾을 수 있는 바닥에서 가장 왼쪽에 있는 노드에 새 노드를 삽입한다고 했을 때, 이때 5는 15의 자식이 된다. 즉, 힙의 균형이 깨진다. 비슷한 이유로 힙에서 삭제할 때도 힙이 균형을 잃지 않도록 항상 마지막 노드를 루트 자리로 넣는 것이다.

균형이 중요한 이유는 $O(logN)$ 안에 연산이 가능하기 때문이다.
불균형이 심한 트리는 순회에 $O(N)$단계가 걸린다.

마지막 노드 문제로 돌아가서, 어떤 힙에서든 일관되게 마지막 노드를 찾는 알고리즘은 무엇일까?
다시 말해, 노드 $N$개를 모두 순회하지 않고도 마지막 노드를 어떻게 찾을 수 있을까?

16.9 배열로 힙 구현하기

마지막 노드 찾기는 힙 연산의 핵심으로, 효율적으로 찾아야하기 때문에 배열을 사용해 힙을 구현한다.

지금까지는 모든 트리가 연결 리스트처럼 링크로 연결된 독립적인 노드로 구성된다고 가정했으나, 배열로도 힙을 구현할 수 있다. 즉, 힙 자체가 내부적으로 배열을 사용하는 추상 데이터 타입일 수 있다.

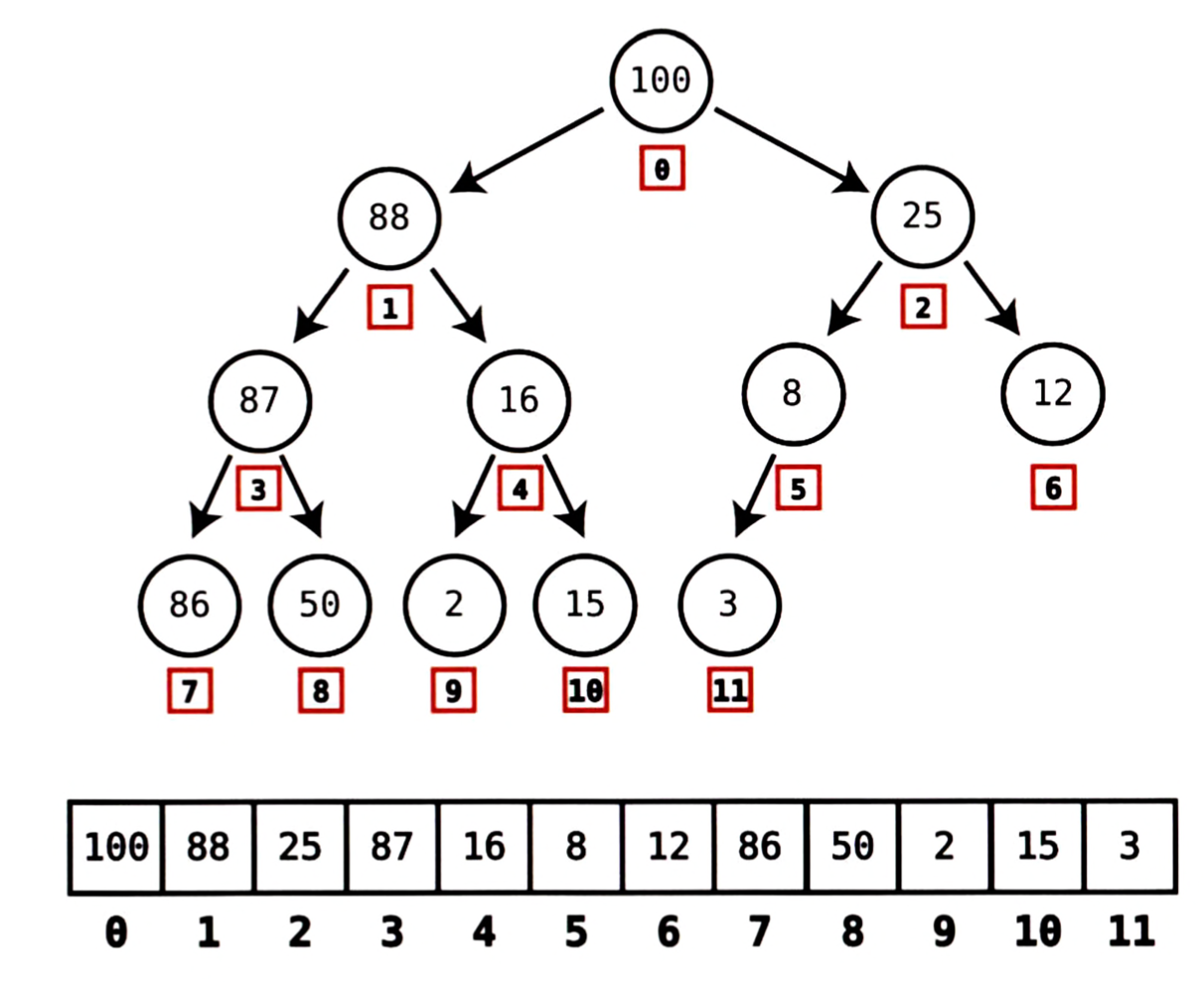
배열로 구현하기 위해 각 노드마다 배열의 인덱스를 할당하는데,
자세히 살펴보면 특정 패턴에 따라 인덱스가 할당됐음을 알 수 있다.

• 루트 노드는 항상 인덱스 0에 저장한다.
• 한 레벨 아래로 내려가 왼쪽에서 오른쪽 방향으로 진행하며 각 노드마다 순서대로 인덱스를 할당한다.

힙을 배열로 구현하는 이유는 '마지막 노드 문제'를 해결하기 위해서다.
위 예제에서 마지막 노드인 3은 배열에 마지막 원소가 된다. 위에서 아래 방향으로, 왼쪽에서 오른쪽 방향으로 이동하며 각 값을 배열에 순서대로 할당하므로 마지막 노드가 항상 배열의 마지막 원소가 된다.

마지막 노드가 항상 배열의 끝에 위치하므로 아주 간단하게 마지막 노드를 찾을 수 있다.
이 원소에 접근하면 되기 때문이다. 뿐만 아니라 새로운 노드를 삽입할 때에도 배열에 끝에 삽입하면 마지막 노드가 바뀌게 된다.

코드로 구현한다면

기본 코드

class Heap {
	constructor() {
    	this.data = [];
    }
  
  	rootNode() {
    	return this.data[0];
    }
  
  	lastNode() {
    	return this.data[this.data.length - 1];
    }
}

해설

class Heap {
	constructor() {
      	// 빈 배열로 힙 초기화
    	this.data = [];
    }
  
  	rootNode() {
      	// 루트 노드는 배열의 첫 번째 원소 반환
    	return this.data[0];
    }
  
  	lastNode() {
      	// 마지막 노드는 배열의 마지막 원소 반환
    	return this.data[this.data.length - 1];
    }
}

배열 기반 힙 순회

힙에서 삽입과 삭제 알고리즘이 가능하려면 힙을 트리클링 할 수 있어야 한다.
그리고 트리클링이 가능하기 위해서는 노드의 부모나 자식에 접근하여 힙을 순회해야 한다.

하지만 단순히 각 노드를 링크로 따라가면 순회가 간단한 트리와는 다르게
배열에서는 어떤 노드와 어떤 노드가 연결되어 있는지 어떻게 알 수 있을까?

앞서 살펴보았던 특정 패턴에 따라 노드에 인덱스를 할당할 경우, 힙은 항상 아래와 같은 특성을 만족한다.

• 어떤 노드의 왼쪽 자식을 찾으려면 (index * 2) + 1 공식을 사용한다.
• 어떤 노드의 오른쪽 자식을 찾으려면 (index * 2) + 2 공식을 사용한다.

위 예제에서 인덱스 4에 위치한 16을 보면, 16의 왼쪽 자식을 찾기 위해서는 $(4 * 2) + 1 = 9$
즉, 인덱스 9에 위치한 2가 해당 노드의 왼쪽 자식이다.

오른쪽 자식도 마찬가지다. $(4 * 2) + 2 = 10$ 이므로 인덱스 10에 위치한 15가 오른쪽 자식이다.

두 공식이 항상 참이므로 트리를 배열로 처리할 수 있다.

자식 노드 인덱스 구하기

leftChildIndex(index) {
	return (index * 2) + 1;
}

rightChildIndex(index) {
	return (index * 2) + 2;
}

다음은 배열 기반 힙의 또 다른 중요한 특성이다.

• 어떤 노드의 부모를 찾으려면 (index - 1) / 2 공식을 사용한다.

이 공식에서는 나눗셈을 사용하여 소숫점 이하를 버린다. (e.g 3/2의 결과는 1.5가 아니라 1이다.)
위 예제에서 인덱스 4의 부모는 $(4 - 1) / 2 = 1$이므로, 인덱스 1에 위치한 88이 부모라는 것을 알 수 있다.

부모 노드 인덱스 구하기

parentIndex(index) {
	return (index - 1) / 2;
}

코드로 구현한다면: 힙 삽입

기본 코드

function insert(value) {
	this.data.push(value);
  
  	let newNodeIndex = this.data.length - 1;

    while (newNodeIndex > 0 && 
           this.data[newNodeIndex] > this.data[parentIndex(newNodeIndex)]) {

        [this.data[parentIndex(newNodeIndex)], this.data[newNodeIndex]] =
        [this.data[newNodeIndex], this.data[parentIndex(newNodeIndex)]];
        newNodeIndex = parentIndex(newNodeIndex);
    }
}

해설

function insert(value) {
	this.data.push(value);
  
  	let newNodeIndex = this.data.length - 1;
    // 다음 루프는 우로 트리클링하는 알고리즘을 실행한다
    // 새 노드가 루트 자리에 없고
    // 새 노드가 부모 노드보다 크면
    while (newNodeIndex > 0 &&
           this.data[newNodeIndex] > this.data[parentIndex(newNodeIndex)]) {
        // 새 노드와 부모 노드를 스왑한다
        [this.data[parentIndex(newNodeIndex)], this.data[newNodeIndex]] =
        [this.data[newNodeIndex], this.data[parentIndex(newNodeIndex)]];
        // 새 노드의 인덱스를 업데이트한다
        newNodeIndex = parentIndex(newNodeIndex);
    }
}

16.10 우선순위 큐로 쓰이는 힙

우선순위 큐의 주요 함수는 큐에서 가장 높은 우선순위를 갖는 항목에 바로 접근하는 것이다.
그래서 우선순위 큐 구현에는 힙이 제격이다.

힙에서는 가장 높은 우선순위의 항목이 항상 루트 노드에 있으니 바로 접근할 수 있다.
가장 높은 우선순위 항목을 처리할 때마다 다음으로 높은 우선순위 항목이 힙의 꼭대기로 오면서 다음 처리 준비를 갖는다. 그리고 이 과정에서 힙은 삽입과 삭제를 아주 빠른 $O(logN)$으로 처리한다.

정렬된 배열과 대조해보면, 정렬된 배열에서는 새로운 값을 올바른 자리에 두는 데 훨씬 느린 $O(N)$ 삽입이 걸린다.

결국 힙의 약한 정렬이 장점으로 작용했다. 완벽한 정렬을 할 필요가 없으니 새로운 값을 $O(logN)$ 시간에 삽입할 수 있음과 동시에 힙은 언제든 필요한 항목에 항상 접근할 수 있을만큼 정렬되어 있다.