너비 우선 탐색(BFS) & 깊이 우선 탐색(DFS)

BFS & DFS?

• 대표적인 그래프 탐색 알고리즘
• DFS, BFS는 모두 노드 수+간선 수 만큼의 복잡도 -> O(n)

📌너비 우선 탐색 (Breadth First Search)

🔎 특징

• 정점들과 같은 레벨에 있는 노드들을 먼저 탐색하는 방식
• 두 개의 큐 사용
• root와 가까운 node들을 찾기 때문에 최단거리 탐색에 유용
• queue에 각 노드 정보를 기록 -> 메모리를 많이 잡아 먹음
• 찾는 target node가 root node와 가깝다고 예상되는 경우 BFS 사용
• 지도 APP의 특정 위치의 최단거리 또는 소셜의 친구 추천 등 사용
  

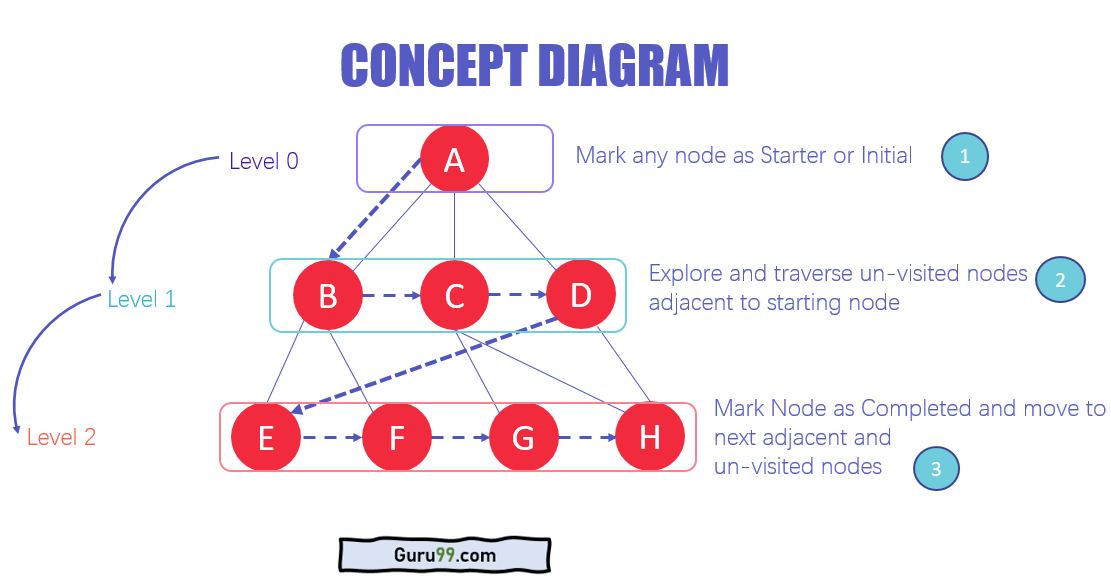
[출처] Guru99.com

• BFS 방식 : A - B - C - D - E - F - G - H

---

📌깊이 우선 탐색 (Depth First Search)

🔎 특징

• 정점의 자식들을 먼저 탐색하는 방식
• 한 개의 큐와 한 개의 스택 사용
• 미로게임 등 경로가 존재 판별 유무에 사용

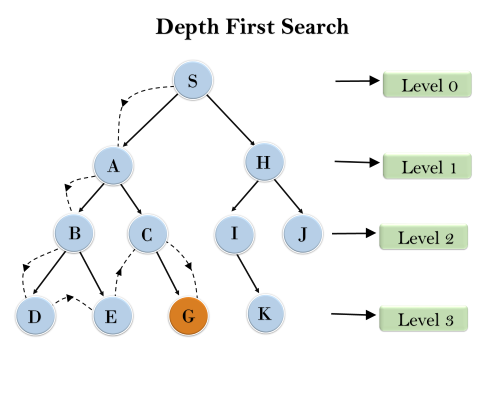
[출처] https://www.javatpoint.com/ai-uninformed-search-algorithms

• DFS 방식 : S - A - B - D - E - C - G - H - I - K - J

---

⌨ 구현

💡 스택 & 큐

스택(stack)

• LIFO(last-In-First_out)
  • 후입선출 구조, 데이터를 추가 할때마다 데이터 마지막에 추가되고, 삭제할 때 마지막에 추가된 데이터가 먼저 삭제
  • 스택에서는 데이터 삽입(push)과 제거(pop)는 스택의 맨 위 한지점에 발생
    • push() : 매개변수 그대로 배열의 마지막 추가한 후 늘어난 배열길이를 반환
    • pop() : 배열의 마지막 데이터를 꺼내 반환, 배열의 길이는 1만큼 줄어듬

큐(Queue)

• FIFO(First-In-First-Out)
  • 선입선출 구조, 목록 마지막에 추가하며, 목록 맨앞에서 데이터를 삭제
  • 큐에서는 shift() 메서드 사용
    • shift() : 배열의 첫 번째 데이터를 꺼내서 반환하며 배열 길이는 1만큼 줄어듬

BFS 알고리즘 구현

• 두 개의 큐(Queue) 활용

const graph = {
  A: ['B', 'C'],
  B: ['A', 'D'],
  C: ['A', 'G', 'H', 'I'],
  D: ['B', 'E', 'F'],
  E: ['D'],
  F: ['D'],
  G: ['C'],
  H: ['C', 'J'],
  I: ['C'],
  J: ['I']
};

const bfsFnc = (graph, startNode) => {
  let resultNode = []; // 탐색이 끝난 노드
  let searchNode = []; // 탐색이 필요한 노드
  
  searchNode.push(startNode); //노드 탐색 시작
  
  while(searchNode.length !== 0) { // 탐색 노드 체크
    const node = searchNode.shift(); // Queue -> FIFO(First-In-First-Out)[선입선출]
    if (!resultNode.includes(node)) {
      // 탐색이 끝난 노드가 아니면 push
      resultNode.push(node);
      searchNode = [...searchNode, ...graph[node]];
    }
  }
  return resultNode;
}

console.log(bfsFnc(graph , "A"));
// ["A", "B", "C", "D", "G", "H", "I", "E", "F", "J"]
  

DFS 알고리즘 구현

• 한 개의 스택(stack)과 한 개의 큐(Queue) 사용
• 자기 자신과 연결되었던 노드들을 먼저 탐색하기 위해 스택(stack) 사용

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"],
};

const dfsFuc = (graph, startNode) => {
  let searchNodeStack = []; // 탐색 노드
  let resultQueue = []; // 탐색이 끝난 노드

  searchNodeStack.push(startNode);

  while (searchNodeStack.length !== 0) {
    // 탐색이 필요한 노드가 있는지 확인
    const node = searchNodeStack.pop(); // Stack -> LIFO(Last-In-First-Out)[후입선출]
    if (!resultQueue.includes(node)) {
      // 탐색한적이 없는 노드 체크
      resultQueue.push(node);
      searchNodeStack = [...searchNodeStack, ...graph[node]];
    }
  }
  return resultQueue;
};

console.log(dfsFuc(graph, "A"));
/// ["A", "C", "I", "J", "H", "G", "B", "D", "F", "E"]