부스트캠프 week7 day2 추가학습 Perplexity, Softmax Loss, GPT1

Dae Hee Lee·2021년 9월 14일

BoostCamp_NLP

목록 보기

10/14

Perplexity

두 모델의 성능을 비교하기 위해 일일히 실제 작업을 시켜보고 정확도를 비교하는 작업을 외부 평가(Extrinsic Evaluation)라고 부른다. 외부 평가는 너무 Cost가 많이 들고, 비교해야하는 모델의 개수가 많아질 수록 시간도 오래 걸리게 된다. 이러한 평가방법보다 어쩌면 조금은 부정확할 수는 있어도 테스트 데이터에 대해서 빠르게 식으로 계산되는 더 간단한 평가 방법이 바로 모델 내에서 자신의 성능을 수치화하여 결과를 내놓는 내부 평가(Intrinsic evaluation)에 해당되는 펄플렉서티(perplexity)이다.

1. 언어 모델의 평가 방법(Eval Metric) : PPL

펄플렉서티(perplexity)는 언어 모델을 평가하기 위한 내부 평가 지표이다. 보통 줄여서 PPL이 라고 표현한다. PPL은 영어에서 'perplexed'는 '헷갈리는'과 유사한 의미를 가진다. 즉, 여기서 PPL은 '헷갈리는 정도'로 이해하면 된다. PPL를 처음 배울때 다소 낯설게 느껴질 수 있는 점이 있다면, PPL은 수치가 높으면 좋은 성능을 의미하는 것이 아니라, '낮을수록' 언어 모델의 성능이 좋다는 것을 의미한다는 점이다.

PPL은 단어의 수로 정규화(normalization) 된 테스트 데이터에 대한 확률의 역수이다. PPL을 최소화한다는 것은 문장의 확률을 최대화하는 것과 같다. 문장 $W$ 의 길이가 $N$ 이라고 하였을 때의 PPL은 다음과 같다.

P P L(W)=P\left(w_{1}, w_{2}, w_{3}, \ldots, w_{N}\right)^{-\frac{1}{N}}=\sqrt[N]{\frac{1}{P\left(w_{1}, w_{2}, w_{3}, \ldots, w_{N}\right)}}

문장의 확률에 체인룰(chain rule)을 적용하면 아래와 같다.

P P L(W)=\sqrt[N]{\frac{1}{P\left(w_{1}, w_{2}, w_{3}, \ldots, w_{N}\right)}}=\sqrt[N]{\frac{1}{\prod_{i=1}^{N} P\left(w_{i} \mid w_{1}, w_{2}, \ldots, w_{i-1}\right)}}

여기에 $n$ -gram을 적용해볼 수도 있다. 예를 들어 bigram 언어 모델의 경우에는 식이 아래와 같다.

P P L(W)=\sqrt[N]{\frac{1}{\prod_{i=1}^{N} P\left(w_{i} \mid w_{i-1}\right)}}

2. 분기 계수(Branching Factor)

PPL은 선택할 수 있는 가능한 경우의 수를 의미하는 분기계수이다. 다시 말해, 언어 모델이 특정 시점에서 평균적으로 몇 개의 선택지를 가지고 고민하고 있는지를 의미한다. 따라서 PPL이 낮은 언어 모델의 성능이 더 좋다고 볼 수 있다.

하지만 PPL의 값이 낮다는 것은 테스트 데이터 상에서 높은 정확도를 보인다는 것이지, 사람이 직접 느끼기에 좋은 언어 모델이라는 것을 반드시 의미하진 않는다. 또한 언어 모델의 PPL은 테스트 데이터에 의존하므로 두 개 이상의 언어 모델을 비교할 때는 정량적으로 양이 많고, 또한 도메인에 알맞은 동일한 테스트 데이터를 사용해야 신뢰도가 높아진다.

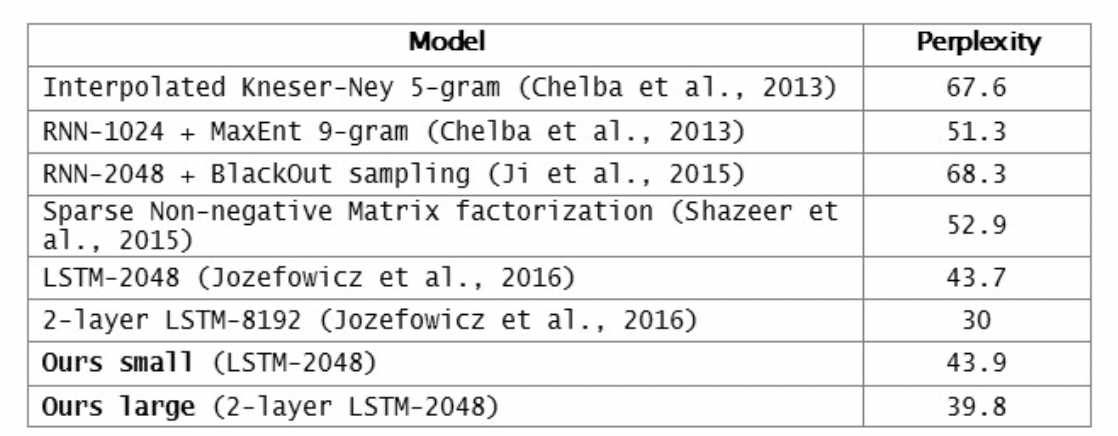
아래 표를 보면 n-gram에 입각한 예전의 언어 모델에 비해 NN을 활용한 모델들이 훨씬 낮은 PPL을 보이는 것을 알 수 있다.

Softmax Loss

이 곳의 글을 참조하였다.
다범주 분류문제를 풀기 위한 딥러닝 모델 말단엔 소프트맥스 함수가 적용된다. 소프트맥스 함수는 범주 수만큼의 차원을 갖는 입력벡터를 받아서 확률값으로로 변환시켜준다. 이후 손실 함수로는 크로스엔트로피(cross entropy)가 쓰이는데, 크로스엔트로피는 소프트맥스 확률의 분포와 정답 분포와의 차이를 나타낸다. 이를 기본으로 해서 손실(오차)을 최소화하는 방향으로 모델의 각 파라메터를 업데이트하는 과정이 바로 딥러닝 모델에서 Softmax Loss를 활용한 학습이다.

그런데 딥러닝 모델 학습시 손실에서 나오는 그래디언트를 계산하는 것이 중요하다. 체인룰(chain rule)에 의해 이 그래디언트에 각 계산 과정에서의 로컬 그래디언트가 끊임없이 곱해져 오차가 역전파(backpropagation)되기 때문이다. 이렇게 손실(오차)에 대한 각 파라메터의 그래디언트를 구하게 되면 그래디언트 디센트(gradient descent) 기법으로 파라메터를 업데이트해 손실을 줄여 나가게 된다.

순전파

분류해야 할 범주의 개수가 n, 소프트맥스 함수의 i번째 입력값을 a라 하면 i번째 출력값 p는 다음과 같이 나타낼 수 있다.

p_i = \frac{exp(a_i)}{\sum_{k}{exp(a_k)}}

또한, 크로스 엔트로피의 관점에서 정답 레이블이 정답 인덱스만 1, 나머지는 0인 원-핫벡터라고 생각하면 아래와 같이 CE Loss를 나타낼 수 있다.

L = -\sum_{j}y_j\ log(p_j)

Gradient

$(1)\ i = j$

\begin{aligned} \frac{\partial p_{i}}{\partial a_{i}} &=\frac{\exp \left(a_{i}\right) \sum_{k} \exp \left(a_{k}\right)-\exp \left(a_{i}\right) \exp \left(a_{i}\right)}{\left(\sum_{k} \exp \left(a_{k}\right)\right)^{2}} \\ \\ &=\frac{\exp \left(a_{i}\right)\left[\sum_{k}\left\{\exp \left(a_{k}\right)\right\}-\exp \left(a_{i}\right)\right]}{\left(\sum_{k} \exp \left(a_{k}\right)\right)^{2}} \\ \\ &=\frac{\exp \left(a_{i}\right)}{\sum_{k} \exp \left(a_{k}\right)} \frac{\sum_{k}\left\{\exp \left(a_{k}\right)\right\}-\exp \left(a_{i}\right)}{\sum_{k} \exp \left(a_{k}\right)} \\ \\ &=\frac{\exp \left(a_{i}\right)}{\sum_{k} \exp \left(a_{k}\right)}\left(1-\frac{\exp \left(a_{i}\right)}{\sum_{k} \exp \left(a_{k}\right)}\right) \\ \\ &=p_{i}\left(1-p_{i}\right) \end{aligned}

$(2)\ i\neq j$

\begin{aligned} \frac{\partial p_{i}}{\partial a_{j}} &=\frac{0-\exp \left(a_{i}\right) \exp \left(a_{j}\right)}{\left(\sum_{k} \exp \left(a_{k}\right)\right)^{2}}\qquad \qquad \qquad \qquad \\ \\ &=-\frac{\exp \left(a_{i}\right)}{\sum_{k} \exp \left(a_{k}\right)} \frac{\exp \left(a_{j}\right)}{\sum_{k} \exp \left(a_{k}\right)} \\ \\ &=-p_{i} p_{j} \end{aligned}

(1), (2)에 의해서 Loss 함수의 Gradient는 다음과 같다.

\begin{aligned} \frac{\partial L}{\partial a_{i}} &=\frac{\partial\left(-\sum_{j} y_{j} \log p_{j}\right)}{\partial a_{i}} \\ &=-\sum_{j} y_{j} \frac{\partial \log p_{j}}{\partial a_{i}} \\ &=-\sum_{j} y_{j} \frac{1}{p_{j}} \frac{\partial p_{j}}{\partial a_{i}} \end{aligned}

위의 식을 정리하면 아래와 같다.

\begin{aligned} -\sum_{j} y_{j} \frac{1}{p_{j}} \frac{\partial p_{j}}{\partial a_{i}} &=-\frac{y_{i}}{p_{i}} p_{i}\left(1-p_{i}\right)-\sum_{i \neq j} \frac{y_{j}}{p_{j}}\left(-p_{i} p_{j}\right) \\ &=-y_{i}+y_{i} p_{i}+\sum_{i \neq j} y_{j} p_{i} \\ &=-y_{i}+\sum_{j} y_{j} p_{i} \\ &=-y_{i}+p_{i} \sum_{j} y_{j} \\ &=p_{i}-y_{i} \end{aligned}

이 때 $y_i$ 라고 하면 정답일 때는 1, 아닐 때는 0의 값을 가지는 것이기 때문에 Loss 함수의 Gradient를 구하는 것은 softmax 출력값에 1 또는 0을 단순히 빼주는 것으로 계산이 가능하다는 것을 알 수 있다.

Generative Pretrained Transformer, GPT

GPT의 학습 방법이나 이론적인 이해를 돕기 위해 정리한 글이다.
이 영상이 많은 도움이 되었다.

"Generative"?, "Language Model"?

GPT는 대표적인 Generative 학습방법을 가지는 언어 모델이다. 보통 기계 학습 분야는 Generative, Discriminative 학습 방법을 가지며 보통 우리가 알던 학습 방법이 후자이다. 후자의 방식은 한정된 Train 데이터에 과적합될 우려가 있다는 단점이 있다. 그러나 Generative 모델은 데이터가 많으면 많을 수록 학습 효과가 뛰어나다. 물론 시간은 오래 걸리겠지만.

또한 언어 모델을 사용하면 Labeling을 하는데 오류가 생기거나 Cost가 소요될 필요가 없다는 장점이 있다. 오로지 막대한 양의 텍스트만 있으면 된다.

Pretrained LM

GPT는 단순한 LM이 아니라 다양한 NLP Task를 해결할 수 있는 모델이다. 학습 방식은 다음의 두 단계를 거친다. 또한, Fine tuning에 있어서 다른 언어 모델은 일련의 선형 변환 결합 이후에 학습을 진행하지만 GPT1은 그러한 과정 없이 Fine-tuning이 가능하다.
1. Unsupervised Pre-training with LM objective function
2. Supervised Fine Tuning

NLI(Natural Language Inference)
QA(Question Answering)
Semantic Similarity
Classification

Transformer

Attention rather than sequence
Parallelization
Encoder - Decoder Architecture
Machine Translation

Skip - connection : 상위층으로 갈수록 입력 토큰들의 의미가 희석되는데, 하위층의 입력 정보를 상위층으로 잘 전달하는 역할을 한다. 또한 Layer가 많은 경우에 대해서 학습 효율성이 커진다.

GPT1

Transformer의 Decoder를 사용하였으며, NLI, QA, Semantic Similarity, Classification등에 사용된다.

Pre-training of Language Model
Unsupervised Learning with unlabeled text
Fine tuning on each specific task

즉, 기존 언어 모델의 Transfer Learning 과정은 Pretrained된 모델에 대하여 Task Specific한 model을 추가한 뒤 Predict하는 것인데, GPT1은 모델 추가 없이 Task에 맞게 지도학습을 통해 학습할 수 있는 것이다. 이를 가능하게 하는 것은 Special Token을 사용했기 때문이다.

또한 GPT1은 기존의 Embedding과 달리 BPE를 이용하여 Embedding해주었다는 차이점이 있다. 기존의 word embedding은 단어 그 자체로 임베딩하기에 신조어나 오탈자 등에 취약하다.

예를 들어 Entailment경우를 생각해보자.