1. 통계 수학의 소개 및 필요성

AI/ML에 대해서 다시 짚어보기

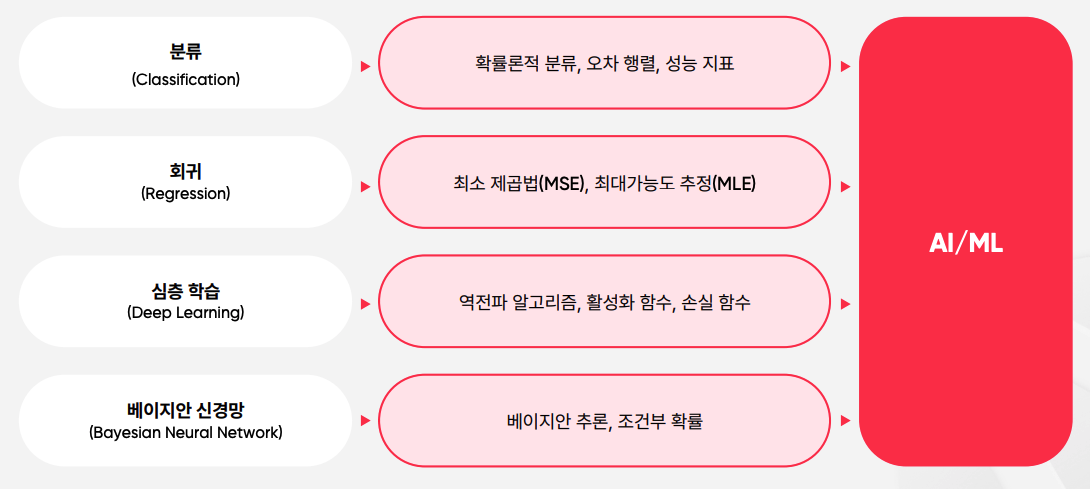
확률/통계론적 관점

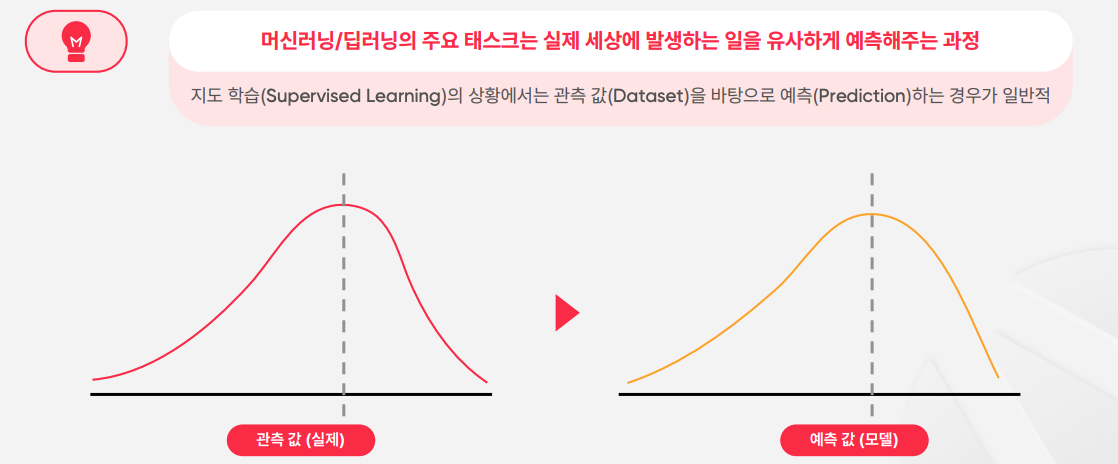
• 머신러닝 모델은 일반적인 개발과 다르게 정확한 정답 데이터를 주지 않음. 대신에 정답치와 유사한 데이터를 준다.
• 그래서 이후에 모델 평가 과정을 거치고, 이 과정을 거쳐서 나온 accuracy 값이 100%가 되는 경우는 거의 없다.

강아지, 고양이 분류 태스크의 확률적 관점

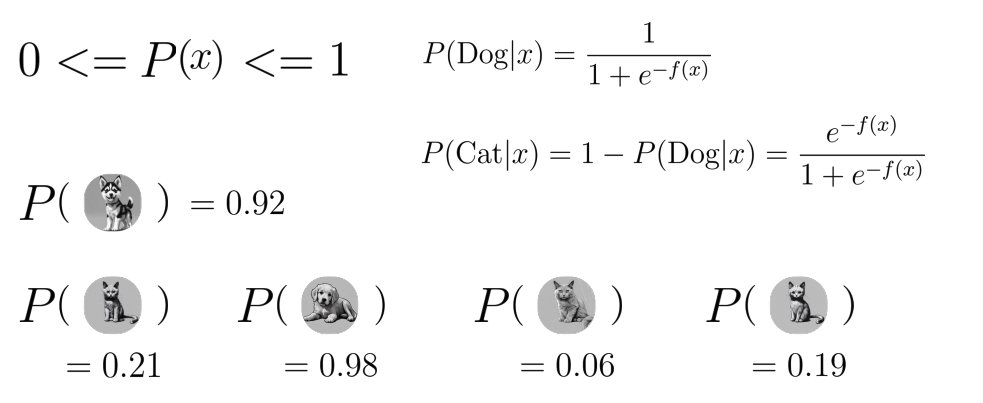
• 강아지에 가까울수록 1, 고양이에 가까울수록 0이 나오는 이진 분류 모델
  • 고양이가 나올 확률은 1에서 강아지가 나올 확률을 뺀 값이랑 같다.
• P라는 함수를 잘 만드는 것이 모델 학습의 과정이고 P의 Output은 얼마나 강아지 또는 고양이에 가까운지 수치적인 값을 만든다. 이 후, 후처리를 통해 해당 Output을 0 또는 1로 만든다.

로지스틱 회귀(Logistic Regression)과 머신러닝의 관계

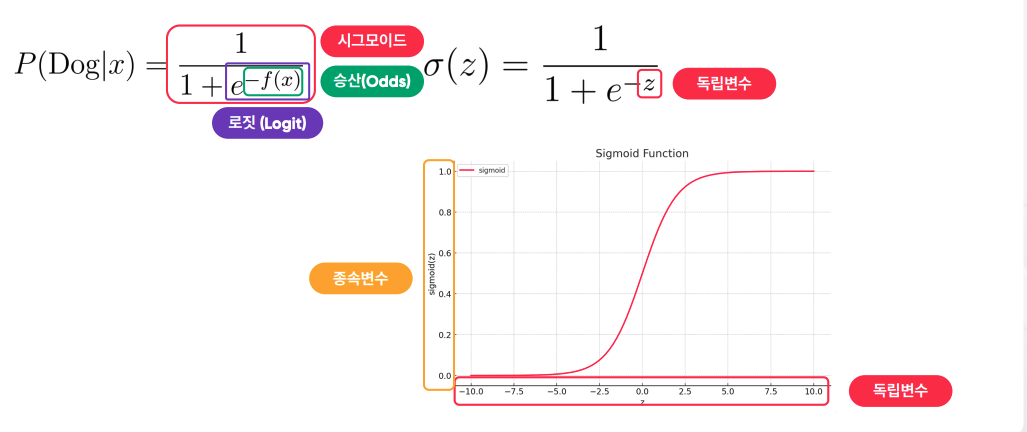
• 시그모이드: 해당 활성화 함수, 0보다 크면 최대 1에 수렴, 0보다 작으면 최소 0에 수렴.
• 독립변수: 해당 그래프의 X 값, 확률에서 제어권을 갖는 변수 무언가가 바뀌었을 때, 확률 결과 값이 독립변수에 의해 바뀜. 우리가 실제로 제어하는 값.
• 종속변수: 독립변수가 바뀜에 의해 바뀌는 값. 해당 그래프의 Y 값.(즉 활성화 함수를 통과했을 때 나오는 Output 값)
• 로짓: 자연상수를 취한 값. 무한대로 발산하는 값을 안정화 시킴.
• 승산: 자연상수 위의 제곱근. 값 범위가 무한대까지로 매우 넒다. 해당 그림에서는 종속변수가 승산이 됨.

코드로 보는 로지스틱 회귀를 이용한 이진 분류

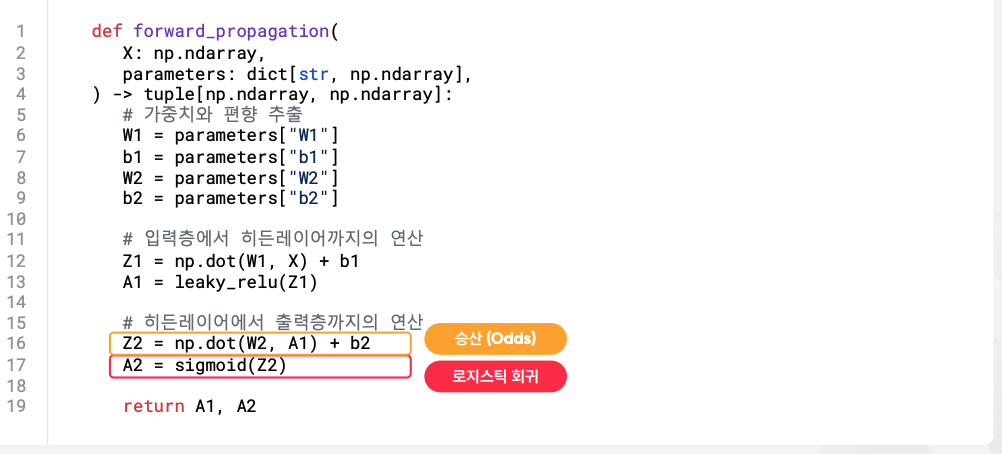
• 종속변수 Z2를 승산으로 두고, 시그모이드 함수를 통한 로지스틱 회귀 기법으로 값을 뽑아낸다.

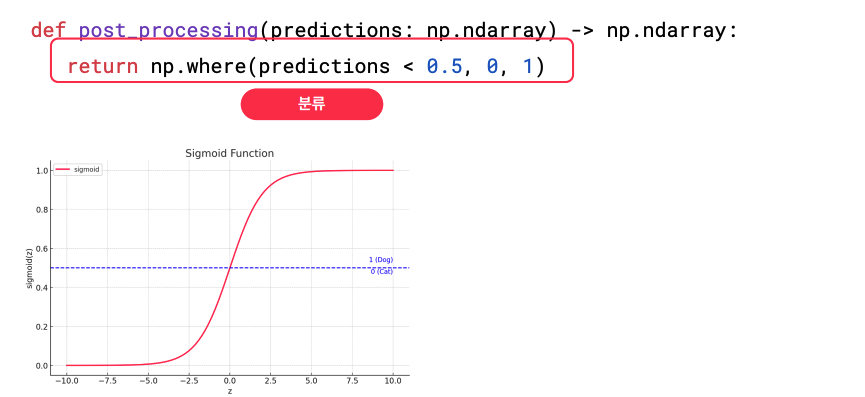
• 로지스틱 회귀를 통과한 값을 predictions라 하면, 이 값을 후처리를 통해 0 또는 1로 취해준다.

확률/통계론적 관점이 어떤 문제를 해결해줄까?

요약

• 확률론적 개념이 AI/ML 관점에서 중요한 이유에 대한 학습
• 모델 관점에서의 확률적 예측치를 얻어내는 과정과 전통적 개발의 차이점 이해
• 로지스틱 회귀 분석에서 사용하는 분류 과정의 확률 관점에서의 이해
• 코드 관점으로 확률론적 관점에서 사용되는 로짓(Logit), 승산(Odds), 시그모이드(Sigmoid)의 이해
• 최종적으로 확률 개념이 AI/ML의 문제를 어떤 접근법으로 해결해주는지에 대한 정리

Reference: 개발자를 위한 MLOps : 추천 시스템 구축부터 최적화까지(FastCampus)