[머신러닝 엔지니어 기본기] 3. MNIST로 시작하는 모델 학습과 서빙

DaeHoon·2024년 3월 20일

개발자를 위한 MLOps: 추천 시스템 구축부터 최적화까지

목록 보기

2/3

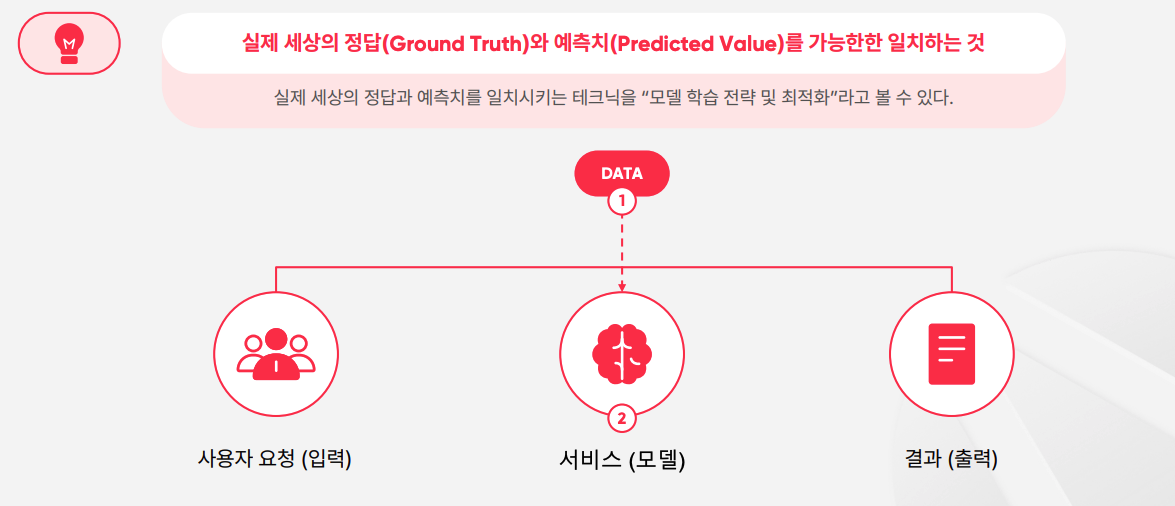
모델 학습의 핵심

MNIST 태스크의 모델 학습

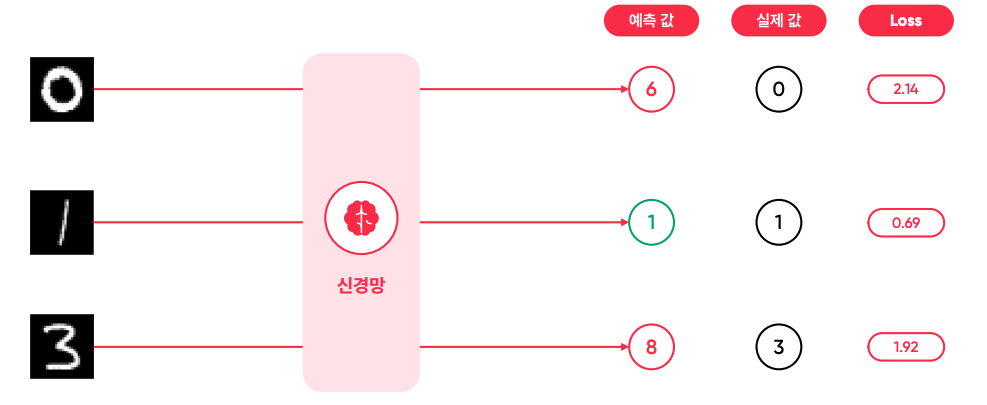
예측이 정확할수록 Loss(오차) 값이 낮아진다.
학습에서는 이 Loss 값을 낮추는 것을 목표로 한다.

MNIST 태스크의 모델 출력

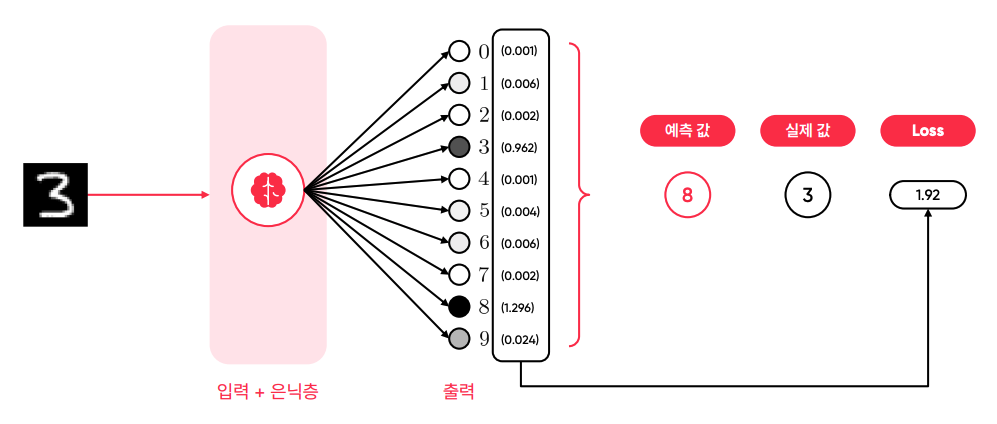
신호의 값(output)이 크면 클수록 검정색에 가까움.
그림을 보면 8의 신호 값이 가장 크다. 8이 줄고 3이 늘어나야 하는 경우
출력의 최종 결과 값(신호)를 실제 값과 비교해서 Loss 값을 뽑아낸다. 이 숫자 값을 패널티로서 역전파 과정을 거친다.
- 예측한 값과 실제 값이 다르면 다를수록 Loss(패널티)는 커지고, 패널티를 크게 줘서 학습 패턴을 크게 변경 시킨다.

Loss Function

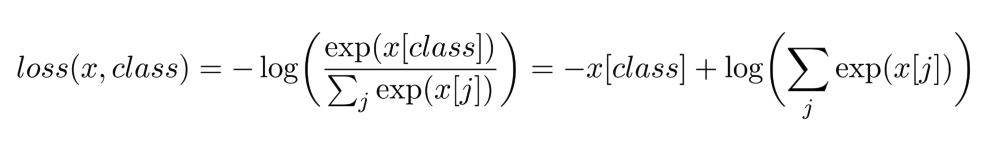
위의 수식은 CrossEntropyLoss 수식. Loss Function 종류 중 하나.
후보군에서 예측 된 확률 분포가 실제 분포와 얼마나 가까운지를 나타내며, CrossEntropyLoss 값을 최소화 시키는 것이 목표.

예시 코드

import torch
import torch.nn as nn

loss_function = nn.CrossEntropyLoss()

loss = loss_function(torch.tensor([[
    0.8982,
    0.805,
    0.6393,
    0.9983,
    0.5731,
    0.0469,
    0.556,
    0.1476,
    1.2404,
    0.5544
]]), torch.LongTensor([3]))
loss.item() # 2.0085251331329346


loss = loss_function(torch.Tensor([[
    3e-5,
    5e-3,
    1e-6,
    0.9204,
    2e-3,
    3e-4,
    5e-4,
    5e-5,
    0.176,
    5e-4
]]), torch.LongTensor([3]))
loss.item() # 1.5401395559310913

loss = loss_function(torch.Tensor([[
    3e-8,
    5e-5,
    1e-6,
    2.4204,
    2e-5,
    3e-5,
    5e-4,
    5e-5,
    6e-4,
    5e-4
]]), torch.LongTensor([3]))
loss.item() # 0.5878590941429138

tensor의 인덱스의 값을 찾는 문제다.
처음의 경우 Index 3의 신호가 낮아 Loss가 약 2로 나왔고, 신호가 크면 클수록 Loss가 낮아진 것을 확인할 수 있다.

Optimization

경사 하강법 (Gradient Descent)

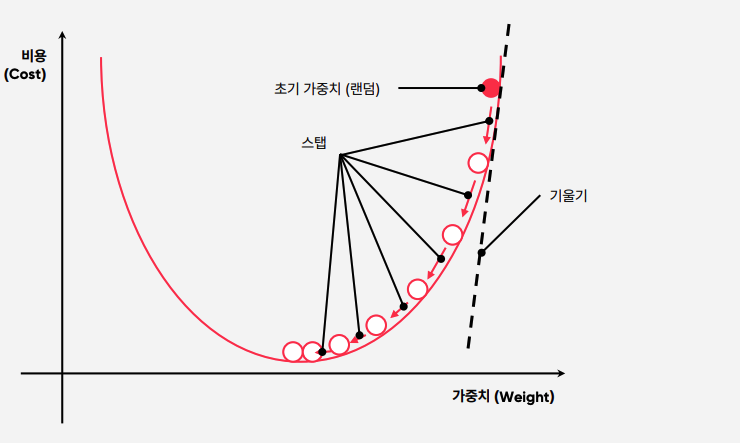
모델 학습 시 최적화 방법 중 하나.
경사 하강법(Gradient descent)은, 1차 근삿값 발견용 최적화 알고리즘으로써, 이 부분의 기본 개념은 함수의 기울기(경사, Gradient)를 구하고 해당 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것을 말합니다. (위키 백과)
기울기가 완만하면(패널티가 적으면) Step이 작아지고, 기울기가 급격하면(패널티가 크면) Step이 커진다.

경사 하강법을 사용하는 이유

일반적으로 경사 하강법은 함수의 최소값을 찾아야 하는 상황에서 사용된다. 머신러닝의 경우 최적의 학습 패턴을 찾기 위해 자신의 파라미터를 검증해야 하며 검증 과정에서 Loss Function을 사용한다. 검증 과정에서 손실 함수의 값이 가장 낮은 파라미터를 발견했다면 해당 파라미터가 최적의 파라미터임이 검증되는 것이다.
그러면 "손실 함수를 미분해서 미분계수가 0인 지점을 찾으면 되지 않을까?"라는 생각을 해 볼 수는 있겠지만 보통 자연 현상에서 마주치는 함수들은 다항함수처럼 간단한 함수가 아닌 대부분 복잡하고 비선형 형태의 패턴을 갖는 함수이며 이러한 함수들은 미분을 통해 계산하기 어려운 경우가 많다. 그래서 경사 하강법을 사용하여 손실 함수의 최소값을 구하게 된다.

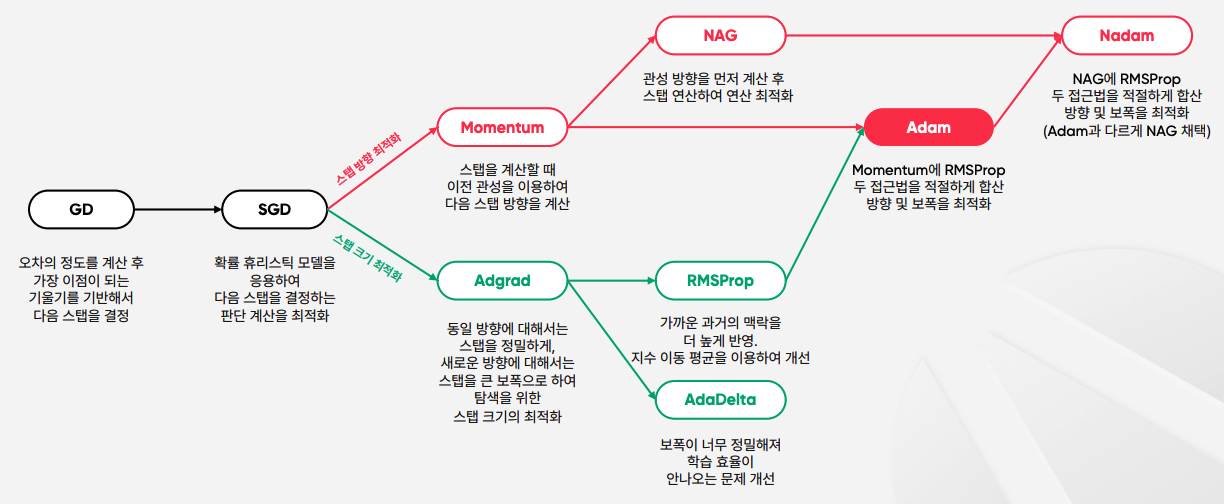
Adam(Adaptive Moment Estimation) Optimizer

모델 최적화 알고리즘 요약

Momentum 와 RMSProp 두가지를 섞어 쓴 알고리즘
즉, 진행하던 속도에 관성을 주고, 최근 경로의 곡면의 변화량에 따른 적응적 학습률을 갖은 알고리즘이고, 매우 넓은 범위의 아키덱처를 가진 서로 다른 신경망에서 잘 작동한다는 것이 증명되어 일반적 알고리즘에 현재 가장 많이 사용되고 있다.

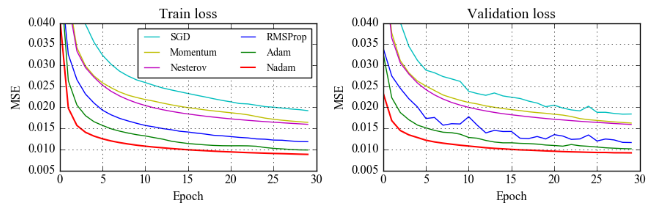
Loss Function을 MSE를 기준으로 한 표인데, Adam에서 파생된 알고리즘이 가장 빨리 Loss가 줄어든다.

Activation Function (활성 함수)

퍼셉트론(Perceptron)의 출력값을 결정하는 비선형(non-linear) 함수
- 즉, 퍼셉트론에서 입력값의 총합을 출력할지 말지 결정하고, 출력한다면 어떤 값으로 변환하여 출력할지 결정하는 함수

활성함수가 왜 필요할까?

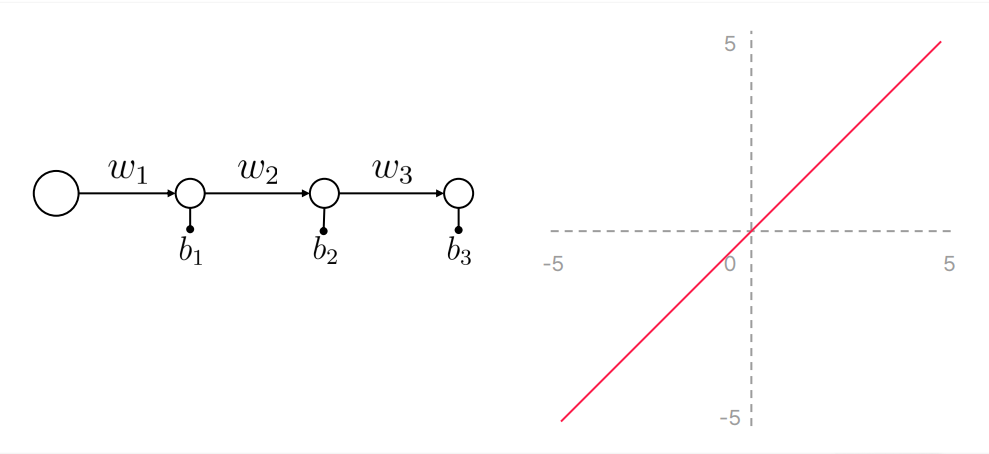
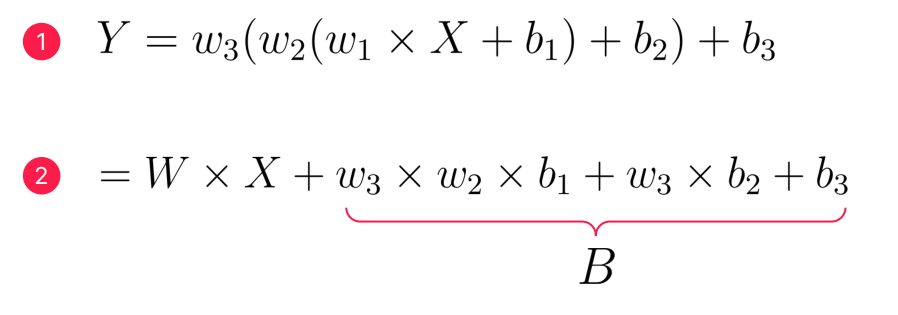
활성함수가 없다면 위의 식처럼 WX+B 라는 Single layer perceptron과 동일한 결과를 낸다.

선형 활성함수의 문제점

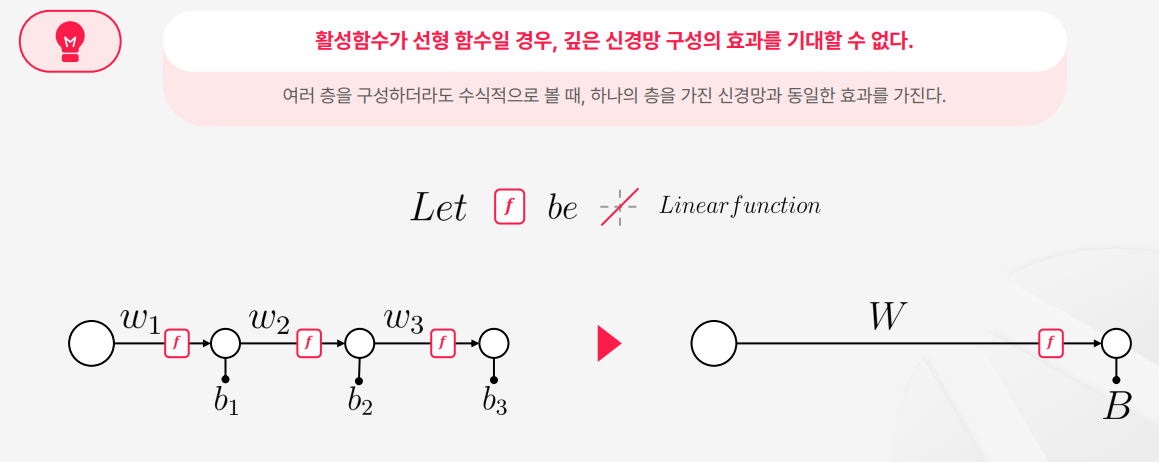
위의 이슈와 마찬가지로 X에 곱해지는 항들은 W로 치환가능하고, 입력과 무관한 상수들은 전체를 B로 치환 가능하기 때문에 WX+B 라는 Single layer perceptron과 동일한 결과를 낸다.

활성함수의 특징

활성함수 종류

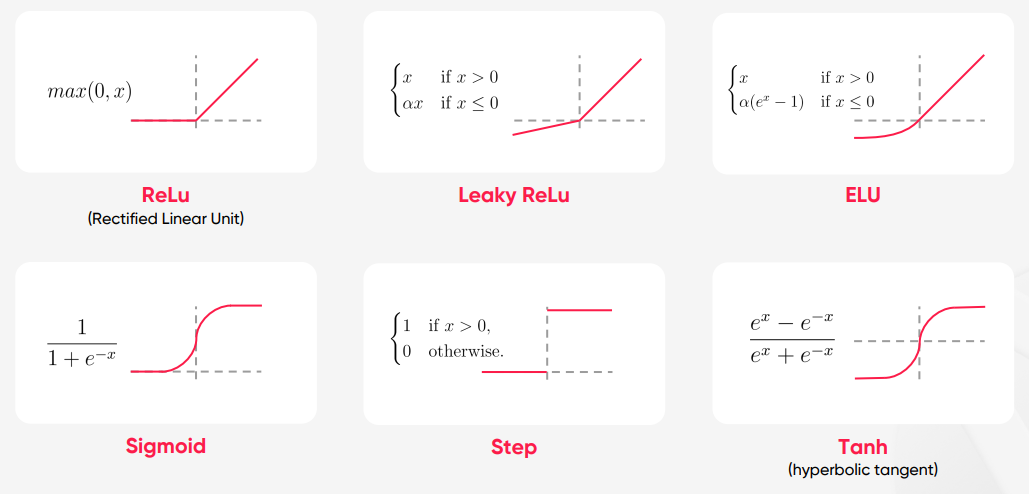
Step

입력이 양수일때는 1(보낸다)을 음수일때는 0(보내지 않는다)의 신호를 보내주는 이진적인(Binary) 함수이다.
직관적이나 모델 Optimization 과정에서 미분을 진행하는데, 미분이 되지않아 사용할 수 없음.

Sigmoid

입력을 (0, 1) 사이의 값으로 normalize 해준다.
이진 분류(binary classification)에서는 자주 사용하지만,Gradient Vanishing 현상이 발생한다.

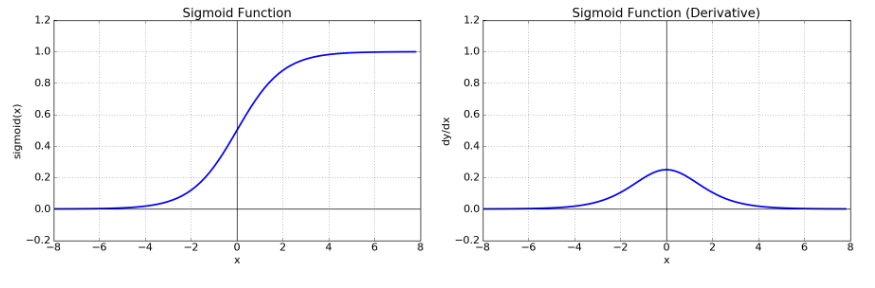
시그모이드의 미분함수를 보면 x=0에서 최대값 1/4를 가지고, input 값이 일정 이상으로 올라가면 미분 값이 0에 수렴하게 된다. 이는 역전파 과정에서 출력 값이 현저하게 감소되는 결과를 낳는다. (0에 가까운 값을 계속 곱하면 0으로 수렴하듯이)
또한 zero-centered 하지 않아 학습이 느려질 수 있다.
- Zero-centered란 그래프의 중심 0인 형태로 함숫값이 양수 혹은 음수에만 치우치지 않고 실수 전체에서 나타나는 형태를 의미한다

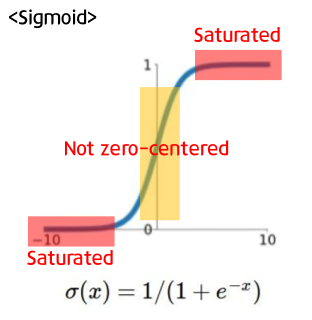
시그모이드 함수의 출력값은 모두 양수기 때문에 경사 하강법 진행 시 기울기가 모두 양수거나 음수가 된다.
- 가령 w1은 작게, w2는 크게 설정하는 것이 최적이라고 할 때 w1은 음의 기울기, w2는 양의 기울기로 따로 지정할 수 없고, 계속 기울기 업데이트가 양수 음수로 지그재르로 변동하는 결과를 가져오고, 학습 효율성을 감소시킨다.

tanh

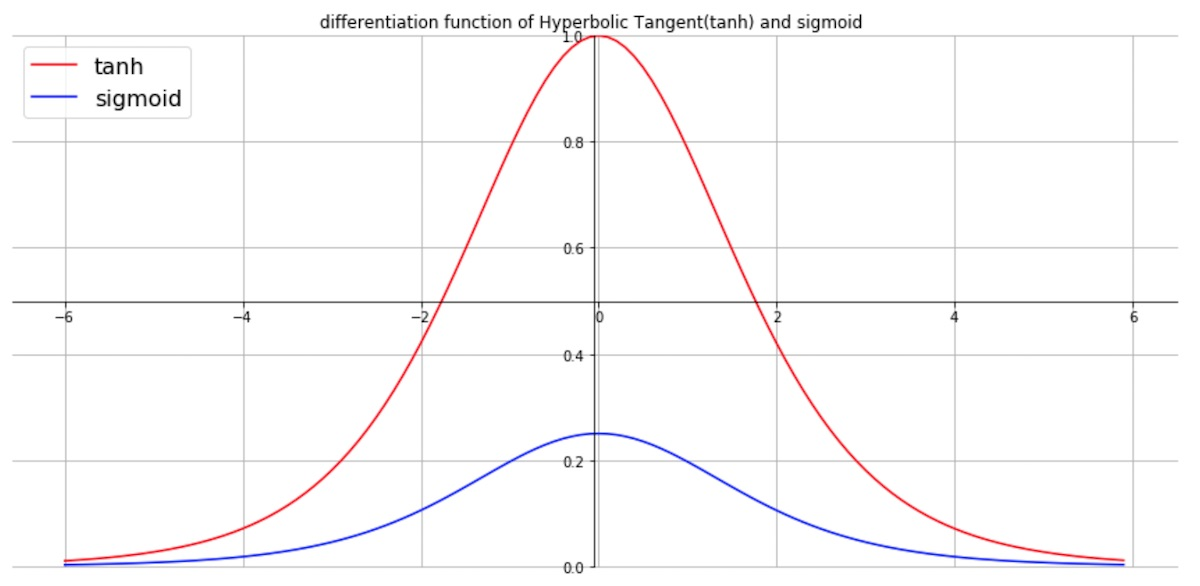
시그모이드 함수를 변형한 쌍곡선 함수.
- tanh 그래프의 미분함수를 보면 최댓값이 1이다. 시그모이드 미분함수와 비교하면 최댓값이 4배가 크다(위에서 시그모이드 미분함수의 최댓값은 1/4임을 밝혔다). 또, 시그모이드 함수의 단점인 non zero-centered를 해결했다. 하지만 여전히 gradient vanishing 문제는 해결하지 못했다.

ReLU

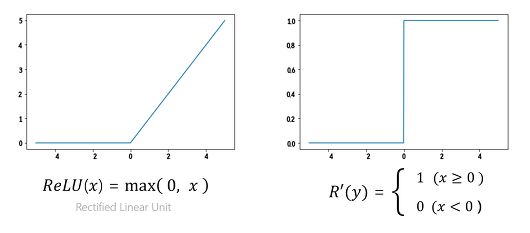
현재 가장 인기있는 활성화 함수인 ReLu는 양수에서 Linear Function과 같으며 음수는 0으로 버려버리는 함수다.
Sparsity : 뉴런의 활성화값이 0인 경우, 다음 레이어로 연결되는 가중치를 곱하더라도 결과값은 0을 나타내게 되서 계산할 필요가 없기에 sparse한 형태가 되고 dense한 형태보다 더 연산량을 월등히 줄여준다.
gradient vanishing 해결: 입출력에 상관없이 0 이상의 입력의 미분 값은 항상 1이다. 더불어 단순히 임계값(0)에 따라 출력값이 결정되므로 연산 속도 또한 빠르다.
Dying ReLU: 입력값이 음수일 경우 미분값은 항상 0이다. 즉, 입력값이 음수인 뉴런은 다시 회생시키기 어렵다는 한계가 존재한다.

Leaky ReLU

Dying ReLU 현상을 해결하기 위해 입력 값이 음수 일 때, 0.001과 같은 매우 작은 값을 출력하도록 설정.

활성함수의 기울기 변화의 문제: Gradient Vanishing

Gradient Vanishing란 역전파(Backpropagation) 과정에서 출력층에서 멀어질수록 Gradient 값이 매우 작아지는 현상을 말한다. 딥러닝 분야에서 Layer를 많이 쌓을수록 데이터 표현력이 증가하기 때문에 학습이 잘 될 것 같지만, 실제로는 Layer가 많아질수록 학습이 잘 되지 않는다.

Sigmoid 함수를 기준으로 예를 들면, 미분값은 0일 때 0.25에 불과하고 x 값이 크거나 작아짐에 따라 기울기는 거의 0에 수렴한다. 즉, 역전파 과정에서 미분값이 거듭 곱해짐면 출력층과 멀어질수록 Gradient 값이 매우 작아질 수 밖에 없다.

순전파 (Feedforward)

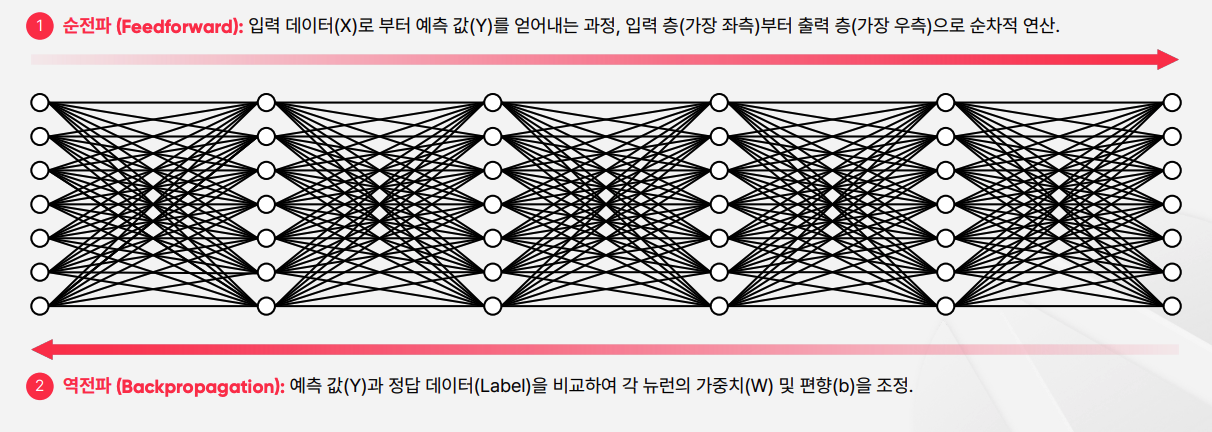
Pytorch를 이용한 MNIST 순전파 코드

class Net(nn.Module):
	def __init__(self, input_size, hidden_size, num_classes):
 		super(Net,self).__init__()
 		self.fc1 = nn.Linear(input_size, hidden_size)
 		self.relu = nn.ReLU()
 		self.fc2 = nn.Linear(hidden_size, num_classes)

def forward(self, x):
 	out = self.fc1(x)
 	out = self.relu(out)
 	out = self.fc2(out)
 	return out

순전파 종류

순방향 신경망 (Feedforward Neural Network)

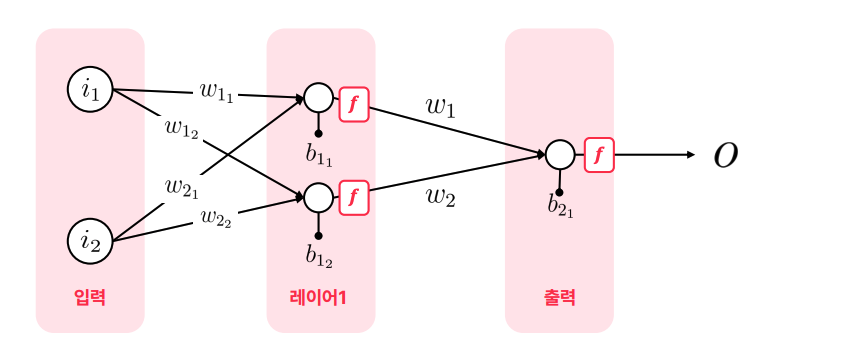
노드 간의 연결이 순환을 형성하지 않는 인공 신경망. 가장 일반적인 신경망 아키텍처

순환 신경망 (Recurrent Neural Network)

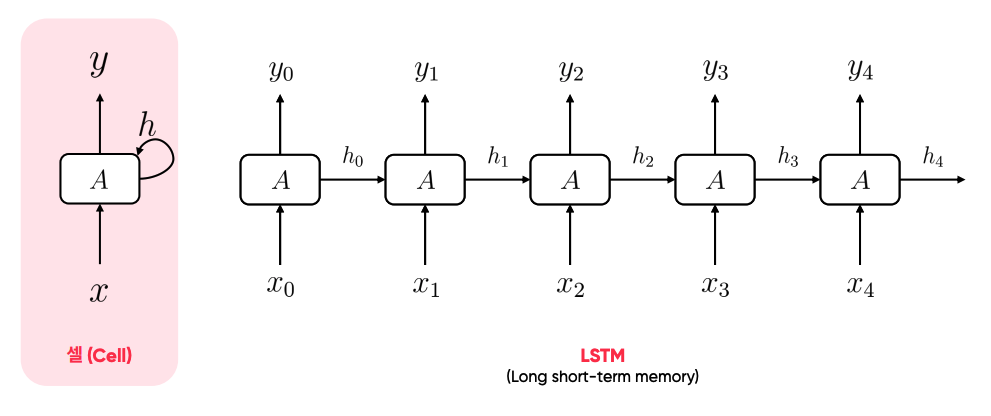
주로 시계열 또는 순차 데이터를 예측하는 딥러닝을 위한 신경망 아키텍처. 은닉층의 메모리 셀에서 나온 값이 다음 은닉층의 메모리 셀에 입력되는 구조
LSTM은 RNN 종류 중 하나다.

역전파 (Backpropagation)

예측 값 Y와 정답 데이터 Label을 비교하여 각 뉴런의 가중치(W) 및 편향(b)을 조정
즉, 역전파는 신경망의 예측치와 실제 정답의 차이 값, Loss를 바탕으로 신경망의 패턴을 재조정하는 과정이다.
- 신경망의 패턴이란, 신경망을 구성하는 각 뉴런들의 가중치(Weight)와 편향(Bias)을 재조정하는 과정을 의미한다.

Pytorch를 이용한 MNIST 학습 코드

for epoch in range(num_epochs):
	for i, (images, labels) in enumerate(train_loader):
    	images = Variable(images.view(-1, 28 * 28)).cuda()
       	labels = Variable(labels).cuda()
       	
        optimizer.zero_grad() #
       	outputs = net(images) # 순전파
       	loss = loss_function(outputs, labels) # loss
      	loss.backward() # 역전파
       	optimizer.step() # 최적화

역전파 순서

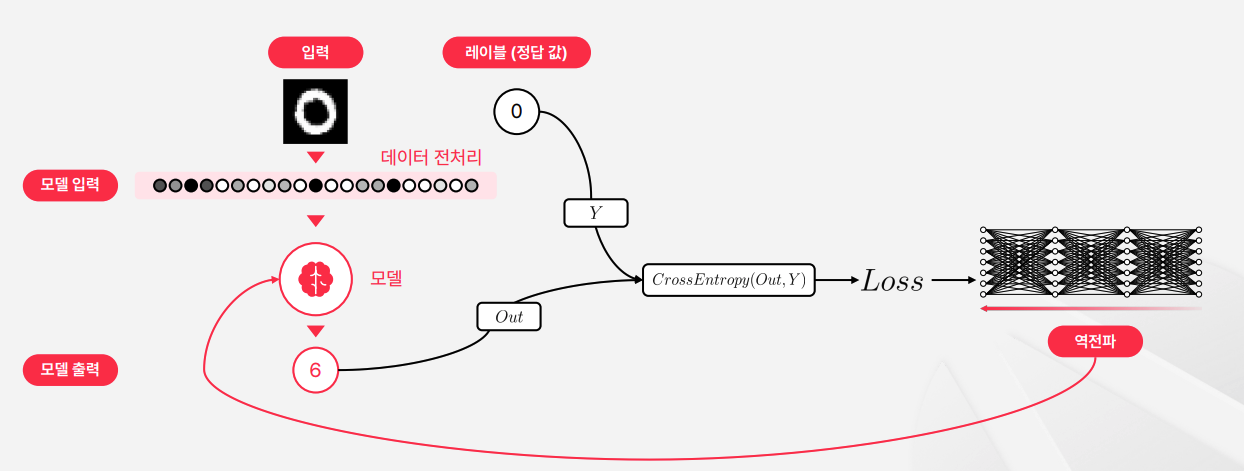
입력의 정답값과 예측한 값을 통해 Loss를 구하고, 역전파 과정에서 가중치(Weight)와 편향(Bias)을 재조정하는 과정을 반복한다.

역전파 원리

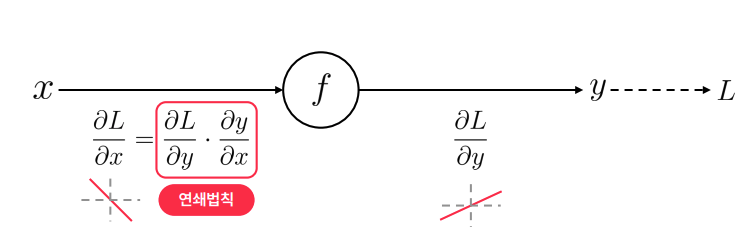
역전파는 합성함수의 도함수를 구하는 과정
- 연결된 뉴런들의 가중치(Weight)와 편향(Bias)을 통해 계산하는 과정은 합성 함수, 이를 역으로 계산하는 과정은 미분의 연쇄법칙을 이용한다.

역전파 연쇄법칙

예시: XOR 예측 문제

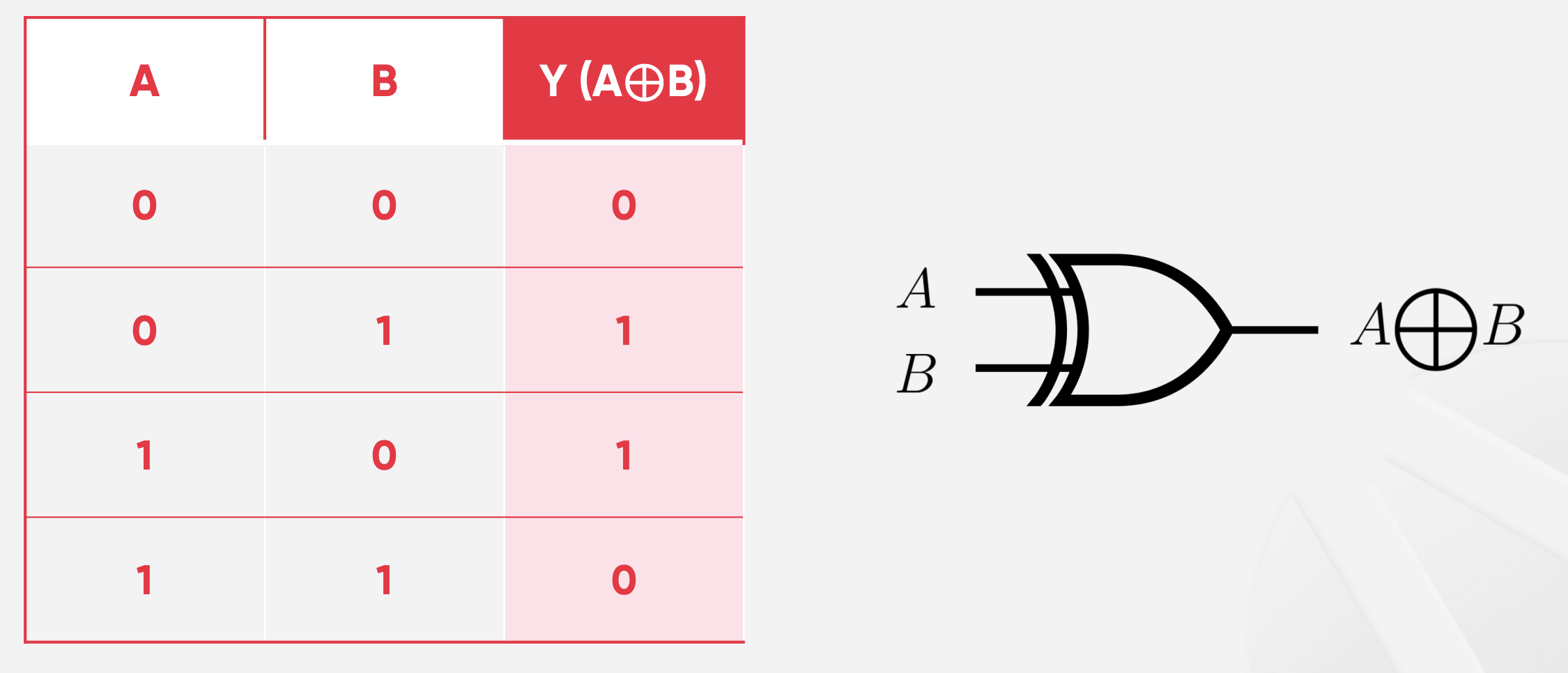
A와 B가 같으면 0, 다르면 1을 출력

XOR 신경망: 순전파

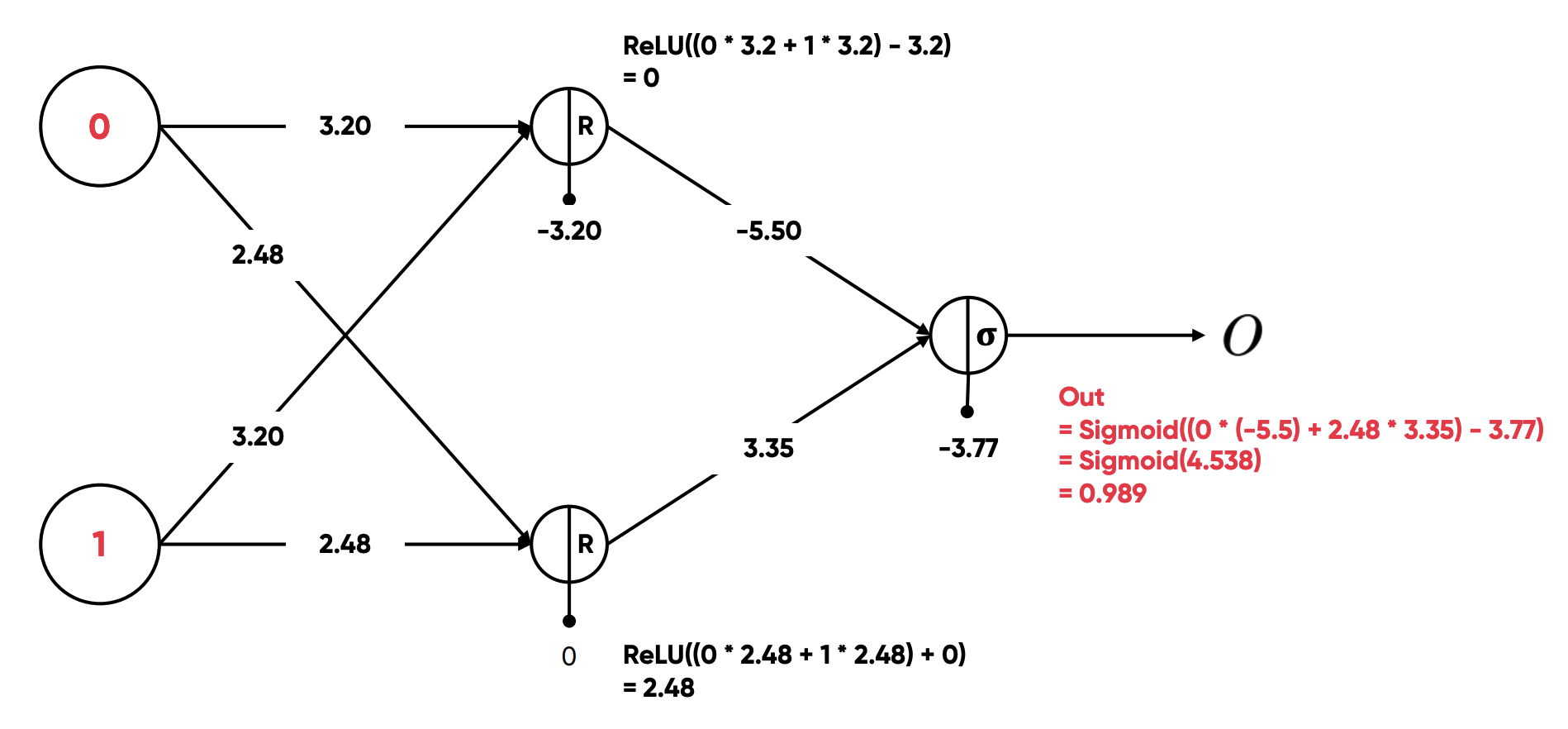
각각의 은닉층 노드에서 Wx + b를 적용하고 Relu 함수를 적용했다. 이 때 x는 이 전 노드의 출력 값이다.
이진 분류를 위해 출력 함수를 Sigmoid 함수로 적용했다.

XOR 신경망: 역전파

출력층 업데이트

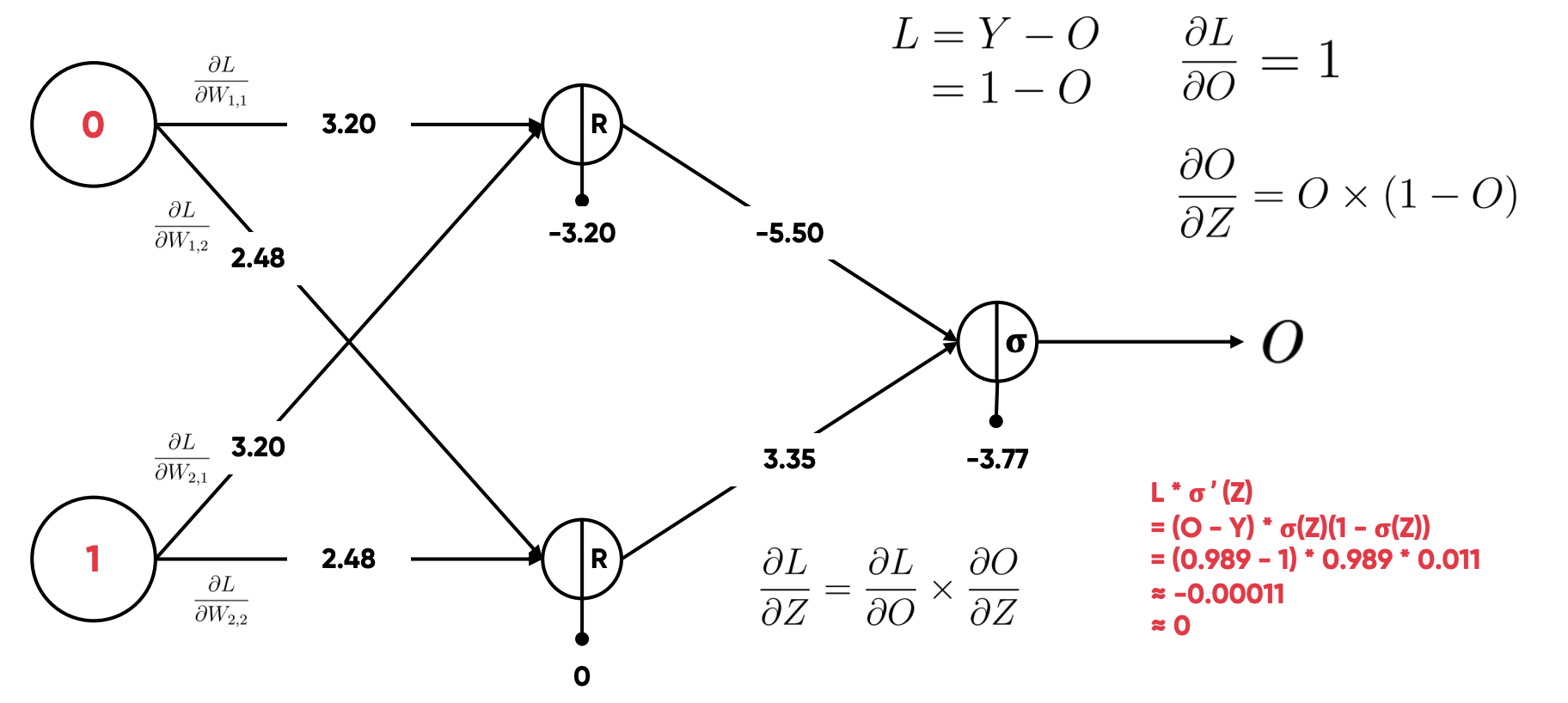
Y: 출력 값, 위의 예시에서는 A와 B가 다르므로 1이다.
O: 모델의 예측 값, 0.989
L: Loss 값
Z: 출력 함수 (Sigmoid)

$\frac{\partial L}{\partial Z} = \frac{\partial L}{\partial O} \times\frac{\partial O}{\partial Z}$ = $(O-y)\times\ O(1 - O)$
- $\frac{\partial L}{\partial O}$ 는 손실 함수인 Binary Cross Entropy 함수 $-y\log(O) - (1-y)\log(1-O)$ 을 미분해서 $-\frac{y}{O} + \frac{1-y}{1-O}$ 가 나온다.
- $\frac{\partial O}{\partial Z}$ 는 Z의 활성화 함수인 Sigmoid 함수 $O = \frac{1}{1+ e^{-z}}$ 를 미분한 $\sigma'(z) = O(1 - O)$ 값이 나온다.
- 즉, 이 두 값을 곱해 $O-y$ 를 구할 수 있다.
위의 식에 O를 대입하면, -0.00011을 구할 수 있고 어림 잡아 0으로 계산했다.

은닉층 업데이트

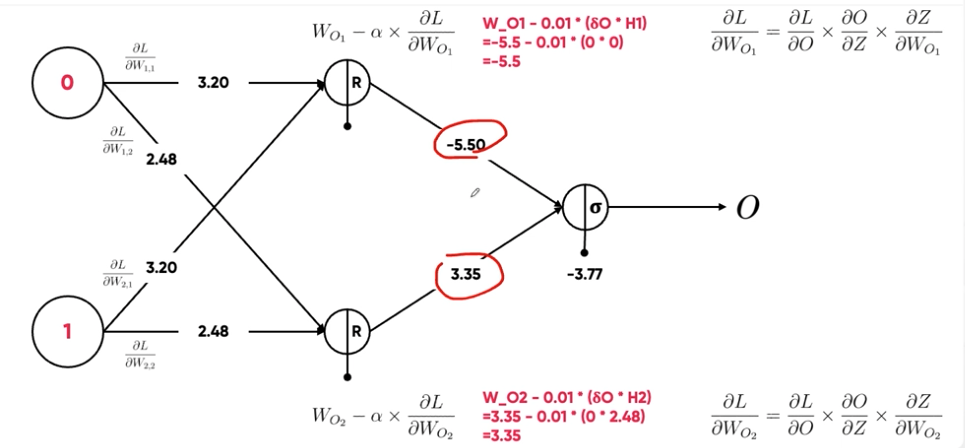
a: Leanring Rate, 해당 예제에서는 0.01
가중치 업데이트: $W_{O_1} - \alpha \times \frac{\partial L}{\partial W_{O_1}}$
편향 업데이트: $B_{O_1} - \alpha \times \frac{\partial L}{\partial B_{O_1}}$

$\frac{\partial L}{\partial W_{O_1}} = \frac{\partial L}{\partial O} \times \frac{\partial O}{\partial Z} \times \frac{\partial Z}{\partial W_{O_1}}$ = $(O-y)\times\ O(1 - O)\times\ X_{1}$
- $\frac{\partial L}{\partial O} \times \frac{\partial O}{\partial Z}$ = $(O-y)\times\ O(1 - O)$
- $\frac{\partial Z}{\partial W_{O_1}} = X_{1}$ 인데, $Z = W_{1}X_{1} + B_{1}$ 이 식을 편미분 한 값이다. 이 값은 아까 위에서 Relu 함수를 통과해서 0으로 구했다.
$\frac{\partial L}{\partial B_{O_1}} = \frac{\partial L}{\partial O} \times \frac{\partial O}{\partial Z} \times \frac{\partial Z}{\partial B_{O_1}}$ = $(O-y)\times\ O(1 - O)$
- $\frac{\partial L}{\partial O} \times \frac{\partial O}{\partial Z}$ = $(O-y)\times\ O(1 - O)$
- $\frac{\partial Z}{\partial B_{O_1}} = 1$ 인데, $Z = W_{1}X_{1} + B_{1}$ 이 식을 편미분 한 값이다.
위에서 구한 값을 대입해보면, 아래의 식을 구할 수 있다.
- 가중치 업데이트: $W_{O_1} - \alpha \times(O-y)\times\ O(1 - O)\times\ X_{1}$
- 편향 업데이트: $B_{O_1} - \alpha \times(O-y)\times\ O(1 - O)$
계산은 위의 사진에서 기입되어 있으니 생략.

Code

위에서 설명한 내용을 직업 구현했고, 이 코드들이 프레임워크 내부에 구현되어 있다고 생각하면 된다.

import numpy as np

def sigmoid(x: np.ndarray) -> np.ndarray:
    return 1 / (1 + np.exp(-x))


def relu(x: np.ndarray) -> np.ndarray:
    return x * (x > 0)


def leaky_relu(x: np.ndarray, alpha: float = 0.01) -> np.ndarray:
    return np.where(x > 0, x, alpha * x)


def post_processing(predictions: np.ndarray) -> np.ndarray:
    return np.where(predictions < 0.5, 0, 1)


def display_results(inputs: np.ndarray, predictions: np.ndarray) -> None:
    processed_predictions = post_processing(predictions)
    print("Input (A, B) | Predicted Y")
    print("---------------------------")
    for i in range(inputs.shape[1]):
        print(f"   {inputs[0, i]}, {inputs[1, i]}    |     {processed_predictions[0, i]}")


def initialize_parameters() -> dict[str, np.ndarray]:
    parameters = {
        "W1": np.random.randn(2, 2),  # 가중치 | INPUT(2 units) -> Hidden Layer(2 units)
        "b1": np.zeros((2, 1)),       # 편향 | Hidden Layer(2 units)
        "W2": np.random.randn(1, 2),  # 가중치 | Hidden Layer(2 units) -> Output(1 unit)
        "b2": np.zeros((1, 1))        # 편향 | Output(1 unit)
    }
    return parameters


def compute_loss(Y: np.ndarray, Y_hat: np.ndarray) -> np.ndarray:
    # BCE (Binary Cross Entropy)
    m = Y.shape[0]
    loss = -np.sum(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)) / m
    return loss


def forward_propagation(
    X: np.ndarray,
    parameters: dict[str, np.ndarray],
) -> tuple[np.ndarray, np.ndarray]:
    # 가중치와 편향 추출
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    # 입력층에서 히든레이어까지의 연산
    Z1 = np.dot(W1, X) + b1
    A1 = leaky_relu(Z1)

    # 히든레이어에서 출력층까지의 연산
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)

    return A1, A2


def backward_propagation(
    parameters: dict[str, np.ndarray],
    A1: np.ndarray,
    A2: np.ndarray,
    X: np.ndarray,
    Y: np.ndarray,
) -> dict[str, np.ndarray]:
    m = X.shape[1]
    W2 = parameters["W2"]

    dZ2 = (A2 - Y) * A2 * (1 - A2)
    dW2 = np.dot(dZ2, A1.T) / m
    db2 = np.sum(dZ2, axis=1, keepdims=True) / m
    dZ1 = np.dot(W2.T, dZ2) * (A1 > 0)
    dW1 = np.dot(dZ1, X.T) / m
    db1 = np.sum(dZ1, axis=1, keepdims=True) / m

    gradients = {
        "dW1": dW1,
        "db1": db1,
        "dW2": dW2,
        "db2": db2
    }

    return gradients


def update_parameters(
    parameters: dict[str, np.ndarray],
    grads: dict[str, np.ndarray],
    learning_rate: float = 6.5,
) -> dict[str, np.ndarray]:
    parameters["W1"] -= learning_rate * grads["dW1"]
    parameters["b1"] -= learning_rate * grads["db1"]
    parameters["W2"] -= learning_rate * grads["dW2"]
    parameters["b2"] -= learning_rate * grads["db2"]

    return parameters


# XOR 문제에 대한 입력과 출력 정의
inputs = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]).T
outputs = np.array([0, 1, 1, 0])

# 파라미터 초기화와 순전파 실행
parameters = initialize_parameters()
predicted_outputs = forward_propagation(inputs, parameters)[1]

# 예측 결과 출력
display_results(inputs, predicted_outputs)

# 200000 Steps, 모델 학습
for i in range(200000):
    A1, A2 = forward_propagation(inputs, parameters)
    grads = backward_propagation(parameters, A1, A2, inputs, outputs)
    parameters = update_parameters(parameters, grads)
    loss = compute_loss(outputs, A2)

    if i > 0 and i % 10000 == 0:
        print(f"{i=}, {loss=}")

predicted_outputs = forward_propagation(inputs, parameters)[1]
print(predicted_outputs)
display_results(inputs, predicted_outputs)

i=10000, loss=0.4365236308924095
i=20000, loss=0.4027903318051978
i=30000, loss=0.3810628217006238
i=40000, loss=0.3659018035794712
i=50000, loss=0.3545317176017809
i=60000, loss=0.3480514836067102
i=70000, loss=0.3401866977059804
i=80000, loss=0.32698877237703583
i=90000, loss=0.3220346350622486
i=100000, loss=0.3169357345859798
i=110000, loss=0.3126991386147929
i=120000, loss=0.3132169521074427
i=130000, loss=0.31970056962151605
i=140000, loss=0.30925423788218825
<ipython-input-75-55413103712b>:38: RuntimeWarning: divide by zero encountered in log
  loss = -np.sum(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)) / m
<ipython-input-75-55413103712b>:38: RuntimeWarning: invalid value encountered in multiply
  loss = -np.sum(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat)) / m
i=150000, loss=0.2984823303547125
i=160000, loss=0.3178656103270632
i=170000, loss=0.29718347070944096
i=180000, loss=0.3095699420136674
i=190000, loss=nan
[[0.02019567 1.         0.44362416 0.51593884]]
Input (A, B) | Predicted Y
---------------------------
   0, 0    |     0
   0, 1    |     1
   1, 0    |     0
   1, 1    |     1

학습을 거칠수록 Loss 값이 떨어지는 것을 확인할 수 있다.

Reference: 개발자를 위한 MLOps : 추천 시스템 구축부터 최적화까지(FastCampus)

DaeHoon

평범한 백엔드 개발자

이전 포스트

[머신러닝 엔지니어 기본기] 1. 머신러닝 엔지니어의 역할과 트랜드

다음 포스트