혼공 머신러닝 + 딥러닝 6장

06 군집 알고리즘

06-1 군집 (Clustering)

• 비지도 학습: 타깃 값이 없는 데이터로 학습을 진행하는 알고리즘. 주로 패턴이나 구조를 발견하는 데 사용

• 넘파이에서 npt 파일 로드: numpy.load() 메서드를 사용하여 .npy 파일을 로드할 수 있습니다. 예를 들어 data = np.load('data.npy')와 같이 사용

• 픽셀 값 분석: 이미지를 배열로 분석할 때, 배열의 계산을 통해 데이터의 특성을 이해할 수 있습니다. 예를 들어, 이미지를 수치적으로 처리하기 위해 픽셀값을 이용

• 평균값과 가까운 사진 고르기: 넘파이의 abs() 함수를 사용하여 배열 간의 차이의 절댓값을 계산할 수 있습니다. 예를 들어, fruits - apple_mean의 절댓값 평균을 계산하여 비슷한 이미지를 찾는 데 사용

• 히스토그램: 데이터를 여러 구간으로 나누어 각 구간에 속한 값들의 빈도를 시각적으로 나타내는 그래프

  • x축: 구간(계급)
  • y축: 발생 빈도(도수)

• 군집 (Clustering): 비슷한 특성을 가진 샘플들을 그룹으로 묶는 비지도 학습의 대표적인 작업입니다. 군집화는 데이터를 이해하고, 분류 전에 데이터를 세분화하는 데 사용됌

---

06-2 K-평균 (K-Means)

• K-평균 알고리즘: 주어진 데이터셋을 K개의 클러스터로 나누는 알고리즘입니다. 처음에는 클러스터 중심을 랜덤하게 정하고, 그 후 클러스터 중심을 업데이트하면서 클러스터를 계속 만들어감.

  • 클러스터 중심 (Centroid): 각 클러스터의 중심은 클러스터에 속한 샘플들의 특성 평균값입니다. 이 중심을 기준으로 샘플들을 다시 배정하고, 클러스터 중심을 갱신하는 방식으로 반복.
  • 반복 과정: 클러스터를 만들고, 중심을 이동시키고, 다시 클러스터를 만드는 과정을 반복하여 최적의 클러스터를 찾음.

• 엘보우 방법 (Elbow Method): 최적의 클러스터 개수를 결정하는 방법 중 하나입니다. 클러스터 개수를 변화시켜가며 이너셔(Inertia)를 측정하고, 이너셔 감소가 꺾이는 지점이 적절한 K 값으로 판단.

  • 이너셔 (Inertia): 각 샘플과 그 클러스터 중심 간의 거리의 제곱 합입니다. 클러스터 수가 늘어날수록 이너셔는 줄어듦.
  • 엘보우 그래프: 클러스터 개수(K)에 따라 이너셔가 감소하는 양상이 나타나는 그래프입니다. 그래프가 꺾이는 지점이 최적의 K 값.

예시 코드 (K-평균)

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 데이터 준비
X = ...  # 데이터셋

# 최적의 클러스터 수를 찾기 위한 엘보우 방법
inertia = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    inertia.append(kmeans.inertia_)

# 엘보우 그래프
plt.plot(range(1, 11), inertia)
plt.xlabel('Number of Clusters')
plt.ylabel('Inertia')
plt.title('Elbow Method')
plt.show()

---

06-3 주성분 분석 (PCA)

• 차원 축소: 원본 데이터에서 중요한 특성을 몇 개의 주요 특성으로 변환하여 차원을 줄이는 과정. 차원 축소는 데이터의 시각화를 용이하게 하고, 모델의 성능을 개선

• 주성분 분석 (PCA): 데이터에서 가장 큰 분산을 가지는 방향을 찾는 알고리즘으로, 이 방향을 주성분이라고 함. 원본 데이터를 주성분에 투영하여 새로운 특성을 생성
  

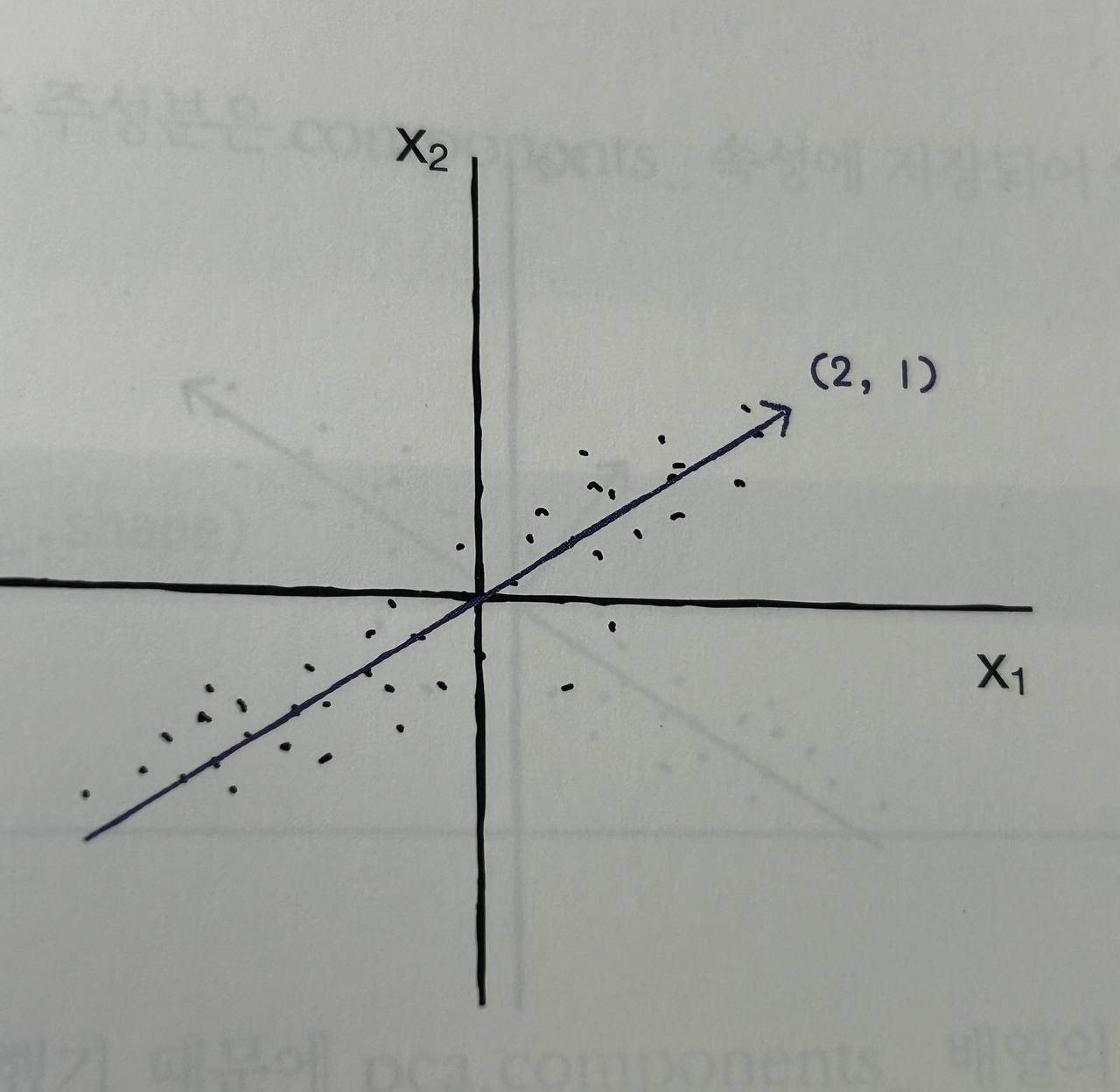
• 설명된 분산: 각 주성분이 데이터의 분산을 얼마나 잘 설명하는지를 나타내는 값

• PCA 클래스: PCA 클래스를 사용하여 주성분 분석을 수행할 수 있음

  • n_components: 추출할 주성분의 수를 지정합니다. 기본값은 None이며, 주성분의 수가 데이터의 차원 수와 동일
  • components_: 훈련된 PCA 모델에서 추출한 주성분들.
  • explained_variance_: 각 주성분이 설명하는 분산의 크기.
  • explained_variance_ratio_: 각 주성분이 전체 분산에서 차지하는 비율.
  • inverse_transform(): 차원 축소된 데이터를 원본 차원으로 복원합니다.
  • 클러스터의 산점도를 잘 구분됌
    

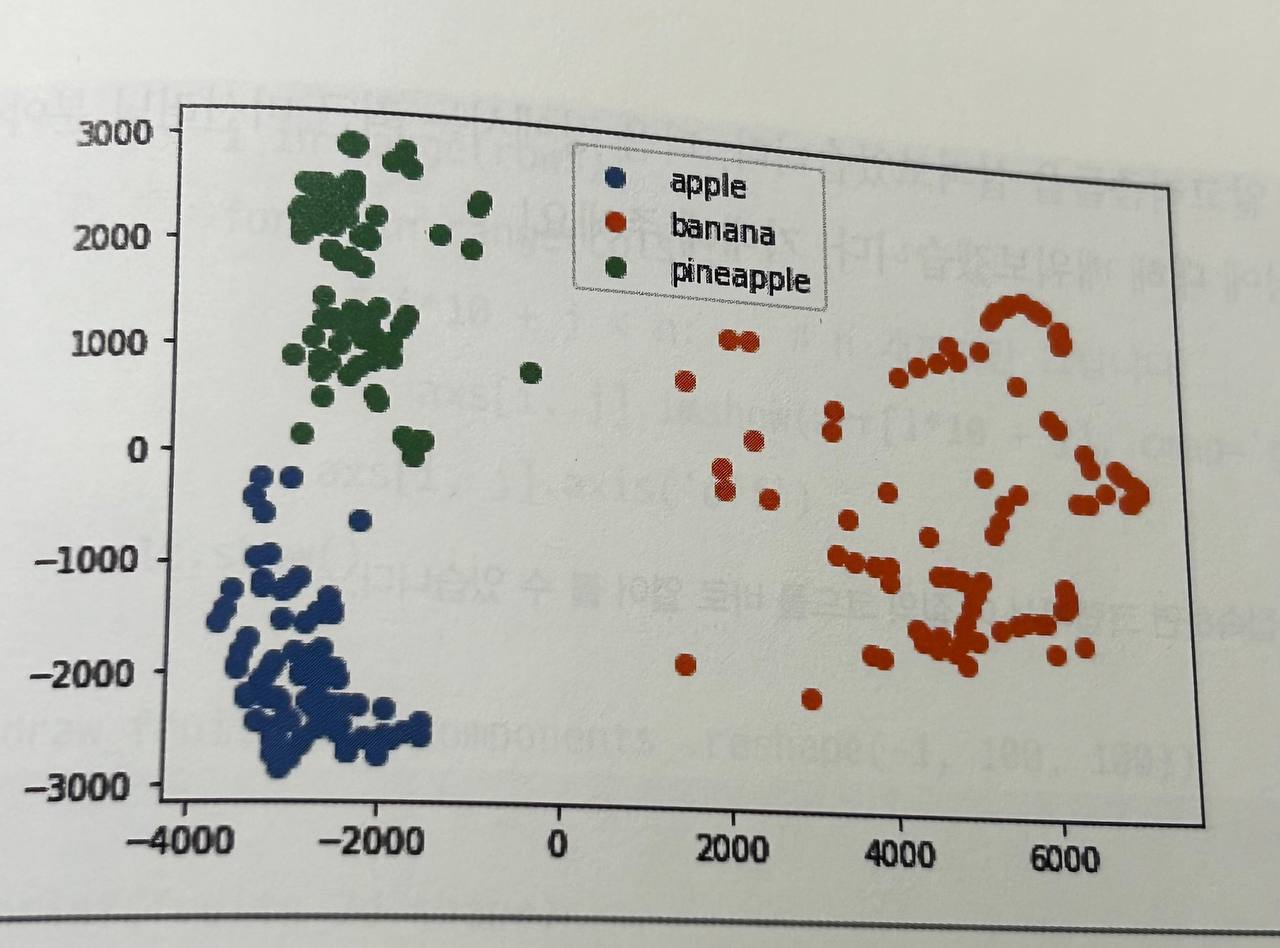
예시 코드 (PCA)

from sklearn.decomposition import PCA

# 데이터 준비
X = ...  # 데이터셋

# PCA 객체 생성
pca = PCA(n_components=2)  # 2개의 주성분으로 차원 축소
X_pca = pca.fit_transform(X)

# 차원 축소된 데이터 출력
print(X_pca)

# 설명된 분산 비율
print(pca.explained_variance_ratio_)

군집 산점도

• 군집화 결과를 시각화하는 데 유용한 방법으로 산점도를 사용합니다. K-평균 군집화나 PCA를 사용하여 데이터를 시각적으로 구분할 수 있습니다.
• 산점도는 각 데이터 포인트를 2D 공간에 플로팅하여 군집을 시각적으로 확인할 수 있게 해줍니다.

예시 코드 (산점도)

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 데이터 준비
X = ...  # 데이터셋

# K-평균 군집화
kmeans = KMeans(n_clusters=3)
y_kmeans = kmeans.fit_predict(X)

# 산점도 시각화
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')

# 군집 중심 표시
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75)
plt.show()