[백준] 1948번 - 임계경로

---

문제 분석

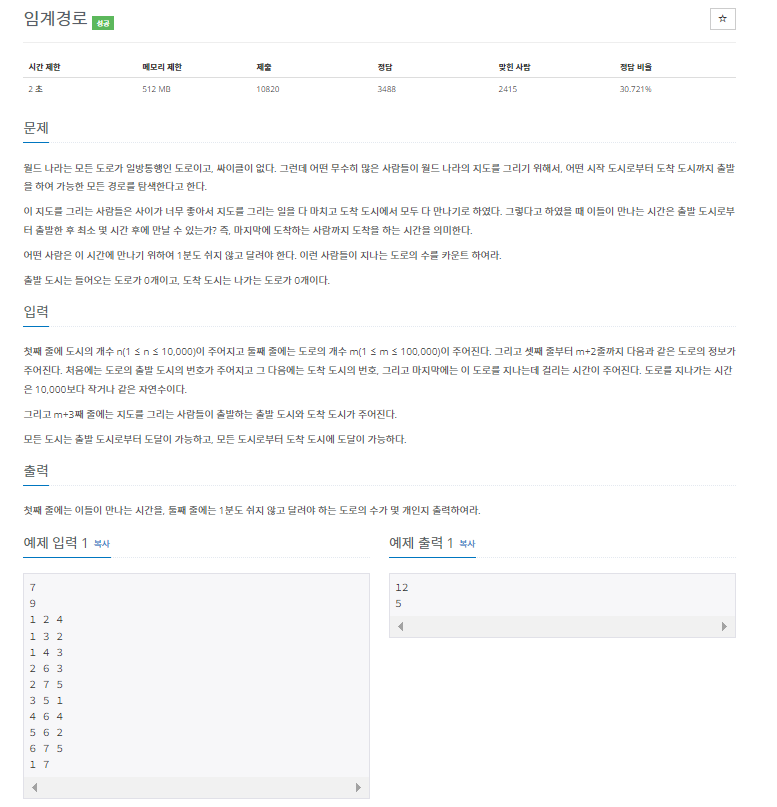
문제에서 모든 노드가 일방통행이고 사이클이 없다라고 하였으므로 위상정렬을 떠올릴 수 있다. 해당 문제는 출발 도시와 도착 도시가 주어지기 때문에 일반적인 위상정렬이 아닌 시작점을 출발 도시로 정하고 위상정렬을 수행하면서 각각의 노드까지의 거리의 최대값을 구하는 과정을 통해 문제를 해결 할 수 있다.
먼저 모든 사람이 도착지에서 만나는 최소의 시간을 구하기 위해서는 각각의 노드까지 걸리는데 소요된 최대 시간을 구하고 최종적으로 도착지점에서의 시간을 반환해주면 된다.
두 번째로 1분도 쉬지 않고 달려야 하는 도로의 수를 구하기 위해서는 에지 뒤집기라는 아이디어를 통해 주어진 경로의 반대의 경로에 해당하는 그래프를 만들고 도착지점부터 출발지까지 오는 과정을 통해 위의 문제를 해결하면 된다.

---

소스 코드

# 임계경로

from collections import deque
import sys
input = sys.stdin.readline

N = int(input())
M = int(input())
arr = [[] for _ in range(N + 1)]
reverseArr = [[] for _ in range(N + 1)]
getPointed = [0 for _ in range(N + 1)]
maxMinute = [0 for _ in range(N + 1)]
visited = [False for _ in range(N + 1)]
queue = deque()
roadCnt = 0

for _ in range(M):
  start, end, minute = map(int, input().split())    
  arr[start].append((end, minute))
  reverseArr[end].append((start, minute))
  getPointed[end] += 1

startCity, endCity = map(int, input().split())

queue.append(startCity)

while queue:
  now = queue.popleft()
  for v in arr[now]:
    getPointed[v[0]] -= 1
    maxMinute[v[0]] = max(maxMinute[v[0]], maxMinute[now] + v[1])

    if getPointed[v[0]] == 0:
      queue.append(v[0])

queue.clear()
queue.append(endCity)
visited[endCity] = True

while queue:
  now = queue.popleft()
  for v in reverseArr[now]:
    if maxMinute[now] == maxMinute[v[0]] + v[1]:
        roadCnt += 1
        if not visited[v[0]]:
          visited[v[0]] = True
          queue.append(v[0])      

print(maxMinute[endCity])
print(roadCnt)